2018—2020年江苏省数学中考试题分类（6）——方程及其应用（含解析） 17页

‎2018—2020年江苏省数学中考试题分类（6）——方程及其应用 一．选择题（共8小题）‎ ‎1．（2020•盐城）把这9个数填入方格中，使其任意一行，任意一列及两条对角线上的数之和都相等，这样便构成了一个“九宫格”．它源于我国古代的“洛書”（图①，是世界上最早的“幻方”．图②是仅可以看到部分数值的“九宫格”，则其中的值为　　‎ A．1 B．3 C．4 D．6‎ ‎2．（2018•无锡）蚊香长度（厘米）与燃烧时间（小时）之间的函数表达式为．则蚊香燃烧的速度是　　‎ A．10厘米小时 B．105厘米小时 ‎ C．10.5厘米小时 D．不能确定 ‎3．（2019•无锡）已知方程组，则的值为　　‎ A． B．2 C．3 D．‎ ‎4．（2019•南通）已知，满足方程组，则的值为　　‎ A．2 B．4 C． D．‎ ‎5．（2020•南京）关于的方程为常数）的根的情况，下列结论中正确的是　　‎ A．两个正根 B．两个负根 ‎ C．一个正根，一个负根 D．无实数根 ‎6．（2019•淮安）若关于的一元二次方程有两个不相等的实数根，则的取值范围是　　‎ A． B． C． D．‎ ‎7．（2019•泰州）方程的两根为、，则等于　　‎ A． B．6 C． D．3‎ ‎8．（2019•盐城）关于的一元二次方程为实数）根的情况是　　‎ A．有两个不相等的实数根 B．有两个相等的实数根 ‎ C．没有实数根 D．不能确定 二．填空题（共21小题）‎ ‎9．（2019•南通）《九章算术》是中国传统数学最重要的著作之一．书中记载：“今有人共买鸡，人出九，盈十一；人出六，不足十六．问人数几何？”意思是：“有若干人共同出钱买鸡，如果每人出九钱，那么多了十一钱；如果每人出六钱，那么少了十六钱．问：共有几个人？”设共有个人共同出钱买鸡，根据题意，可列一元一次方程为　　．‎ ‎10．（2018•南通）古代名著《算学启蒙》中有一题：良马日行二百四十里．驽马日行一百五十里．驽马先行一十二日，问良马几何追及之．意思是：跑得快的马每天走240里，跑得慢的马每天走150里．慢马先走12天，快马几天可追上慢马？若设快马天可追上慢马，则由题意，可列方程为　　．‎ ‎11．（2020•南京）已知、满足方程组，则的值为　　．‎ ‎12．（2020•无锡）我国古代问题：以绳测井，若将绳三折测之，绳多四尺，若将绳四折测之，绳多一尺，井深几何？这段话的意思是：用绳子量井深，把绳三折来量，井外余绳四尺，把绳四折来量，井外余绳一尺，井深几尺？则该问题的井深是　　尺．‎ ‎13．（2019•常州）若是关于、的二元一次方程的解，则　　．‎ ‎14．（2019•苏州）若，，则的值为　　．‎ ‎15．（2019•宿迁）下面3个天平左盘中“△”“□”分别表示两种质量不同的物体，则第三个天平右盘中砝码的质量为　　．‎ ‎16．（2018•淮安）若关于、的二元一次方程有一个解是，则　　．‎ ‎17．（2018•无锡）方程组的解是　　．‎ ‎18．（2020•南通）1275年，我国南宋数学家杨辉在《田亩比类乘除算法》中提出这样一个问题：直田积八百六十四步，只云阔不及长一十二步．问阔及长各几步．意思是：矩形面积864平方步，宽比长少12步，问宽和长各几步．若设长为步，则可列方程为　　．‎ ‎19．（2020•南通）若，是方程的两个实数根，则代数式的值等于　　．‎ ‎20．（2020•镇江）一元二次方程的两根分别为　　．‎ ‎21．（2020•常州）若关于的方程有一个根是1，则　　．‎ ‎22．（2020•泰州）方程的两根为、，则的值为　　．‎ ‎23．（2020•扬州）方程的根是　　．‎ ‎24．（2019•镇江）若关于的方程有两个相等的实数根，则实数的值等于　　．‎ ‎25．（2019•南京）已知是关于的方程的一个根，则　　．‎ ‎26．（2019•盐城）设、是方程的两个根，则　　．‎ ‎27．（2019•连云港）已知关于的一元二次方程有两个相等的实数根，则的值等于　　．‎ ‎28．（2019•扬州）一元二次方程的根是　　．‎ ‎29．（2019•徐州）方程的解是　　．‎ 三．解答题（共17小题）‎ ‎30．（2018•镇江）小李读一本名著，星期六读了36页，第二天读了剩余部分的，这两天共读了整本书的，这本名著共有多少页？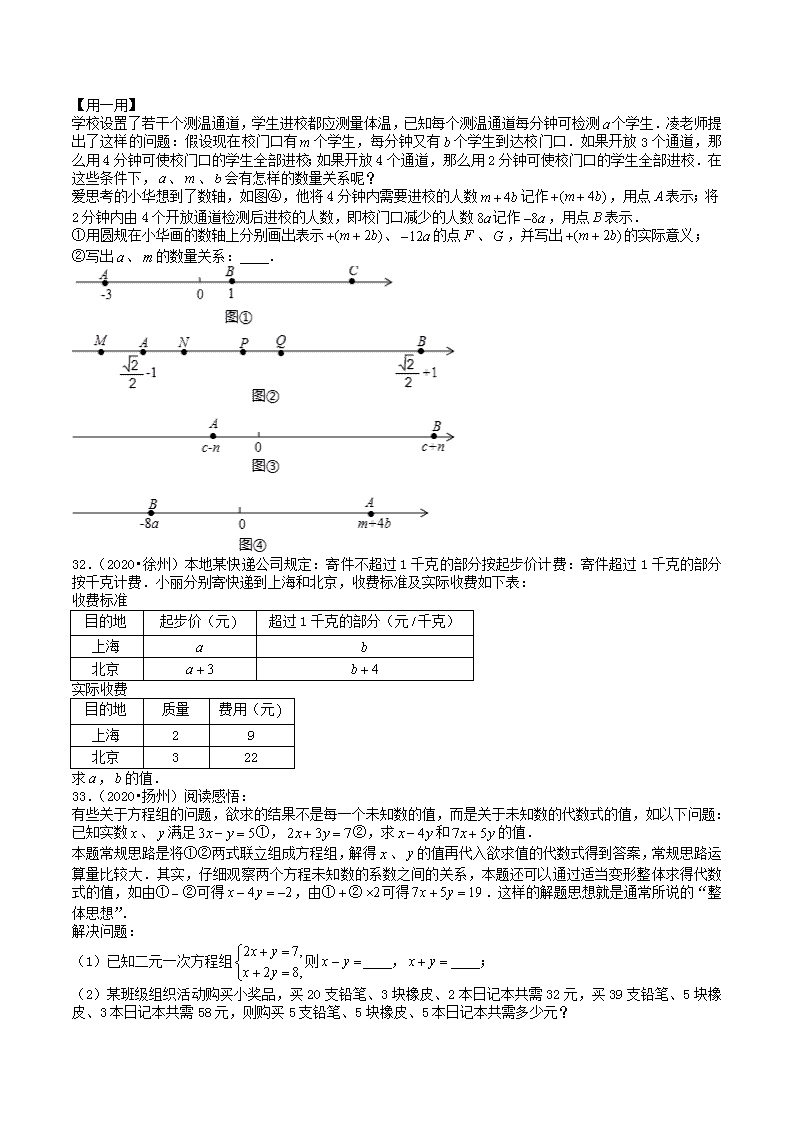‎ ‎31．（2020•镇江）【算一算】‎ 如图①，点、、在数轴上，为的中点，点表示，点表示1，则点表示的数为　　，长等于　　；‎ ‎【找一找】‎ 如图②，点、、、中的一点是数轴的原点，点、分别表示实数、，是的中点，则点　　是这个数轴的原点；‎ ‎【画一画】‎ 如图③，点、分别表示实数、，在这个数轴上作出表示实数的点（要求：尺规作图，不写作法，保留作图痕迹）；‎ ‎【用一用】‎ 学校设置了若干个测温通道，学生进校都应测量体温，已知每个测温通道每分钟可检测个学生．凌老师提出了这样的问题：假设现在校门口有个学生，每分钟又有个学生到达校门口．如果开放3个通道，那么用4分钟可使校门口的学生全部进校；如果开放4个通道，那么用2分钟可使校门口的学生全部进校．在这些条件下，、、会有怎样的数量关系呢？‎ 爱思考的小华想到了数轴，如图④，他将4分钟内需要进校的人数记作，用点表示；将2分钟内由4个开放通道检测后进校的人数，即校门口减少的人数记作，用点表示．‎ ‎①用圆规在小华画的数轴上分别画出表示、的点、，并写出的实际意义；‎ ‎②写出、的数量关系：　　．‎ ‎32．（2020•徐州）本地某快递公司规定：寄件不超过1千克的部分按起步价计费：寄件超过1千克的部分按千克计费．小丽分别寄快递到上海和北京，收费标准及实际收费如下表：‎ 收费标准 ‎ 目的地 起步价（元 超过1千克的部分（元千克）‎ 上海 北京 实际收费 ‎ 目的地 质量 费用（元 上海 ‎2‎ ‎9‎ 北京 ‎3‎ ‎22‎ 求，的值．‎ ‎33．（2020•扬州）阅读感悟：‎ 有些关于方程组的问题，欲求的结果不是每一个未知数的值，而是关于未知数的代数式的值，如以下问题：‎ 已知实数、满足①，②，求和的值．‎ 本题常规思路是将①②两式联立组成方程组，解得、的值再代入欲求值的代数式得到答案，常规思路运算量比较大．其实，仔细观察两个方程未知数的系数之间的关系，本题还可以通过适当变形整体求得代数式的值，如由①②可得，由①②可得．这样的解题思想就是通常所说的“整体思想”．‎ 解决问题：‎ ‎（1）已知二元一次方程组则　　，　　；‎ ‎（2）某班级组织活动购买小奖品，买20支铅笔、3块橡皮、2本日记本共需32元，买39支铅笔、5块橡皮、3本日记本共需58元，则购买5支铅笔、5块橡皮、5本日记本共需多少元？‎ ‎（3）对于实数、，定义新运算：，其中、、是常数，等式右边是通常的加法和乘法运算．已知，，那么　　．‎ ‎34．（2020•淮安）某停车场的收费标准如下：中型汽车的停车费为15元辆，小型汽车的停车费为8元辆．现在停车场内停有30辆中、小型汽车，这些车共缴纳停车费324元，求中、小型汽车各有多少辆？‎ ‎35．（2020•连云港）解方程组 ‎36．（2019•淮安）某公司用火车和汽车运输两批物资，具体运输情况如下表所示：‎ 所用火车车皮数量（节 所用汽车数量（辆 运输物资总量（吨 第一批 ‎2‎ ‎5‎ ‎130‎ 第二批 ‎4‎ ‎3‎ ‎218‎ 试问每节火车车皮和每辆汽车平均各装物资多少吨？‎ ‎37．（2019•盐城）体育器材室有、两种型号的实心球，1只型球与1只型球的质量共7千克，3只型球与1只型球的质量共13千克．‎ ‎（1）每只型球、型球的质量分别是多少千克？‎ ‎（2）现有型球、型球的质量共17千克，则型球、型球各有多少只？‎ ‎38．（2018•扬州）对于任意实数，，定义关于“”的一种运算如下：．例如．‎ ‎（1）求的值；‎ ‎（2）若，且，求的值．‎ ‎39．（2018•宿迁）解方程组：．‎ ‎40．（2020•徐州）（1）解方程：；‎ ‎（2）解不等式组：．‎ ‎41．（2020•无锡）解方程：‎ ‎（1）；‎ ‎（2）．‎ ‎42．（2020•南京）解方程：．‎ ‎43．（2019•无锡）（1）解方程：；‎ ‎（2）解不等式组：．‎ ‎44．（2019•徐州）如图，有一块矩形硬纸板，长，宽．在其四角各剪去一个同样的正方形，然后将四周突出部分折起，可制成一个无盖长方体盒子．当剪去正方形的边长取何值时，所得长方体盒子的侧面积为？‎ ‎45．（2019•南京）某地计划对矩形广场进行扩建改造．如图，原广场长，宽，要求扩充后的矩形广场长与宽的比为．扩充区域的扩建费用每平方米30元，扩建后在原广场和扩充区域都铺设地砖，铺设地砖费用每平方米100元．如果计划总费用642000元，扩充后广场的长和宽应分别是多少米？‎ ‎46．（2019•无锡）解方程：‎ ‎（1）；‎ ‎（2）．‎ ‎2018—2020年江苏省数学中考试题分类（6）——方程及其应用 一．选择题（共8小题）‎ ‎1．（2020•盐城）把这9个数填入方格中，使其任意一行，任意一列及两条对角线上的数之和都相等，这样便构成了一个“九宫格”．它源于我国古代的“洛書”（图①，是世界上最早的“幻方”．图②是仅可以看到部分数值的“九宫格”，则其中的值为　　‎ A．1 B．3 C．4 D．6‎ ‎【解答】解：由题意，可得，‎ 解得．‎ 故选：．‎ ‎2．（2018•无锡）蚊香长度（厘米）与燃烧时间（小时）之间的函数表达式为．则蚊香燃烧的速度是　　‎ A．10厘米小时 B．105厘米小时 ‎ C．10.5厘米小时 D．不能确定 ‎【解答】解：设时间时蚊香长度为，时间时蚊香长度为 ‎，‎ ‎ 则：速度 蚊香燃烧的速度是10厘米小时 故选：．‎ ‎3．（2019•无锡）已知方程组，则的值为　　‎ A． B．2 C．3 D．‎ ‎【解答】解：由方程组可得：，‎ 则，‎ 故选：．‎ ‎4．（2019•南通）已知，满足方程组，则的值为　　‎ A．2 B．4 C． D．‎ ‎【解答】解：，‎ ‎①②得：，‎ 则，‎ 故选：．‎ ‎5．（2020•南京）关于的方程为常数）的根的情况，下列结论中正确的是　　‎ A．两个正根 B．两个负根 ‎ C．一个正根，一个负根 D．无实数根 ‎【解答】解：关于的方程为常数），‎ ‎，‎ ‎△，‎ 方程有两个不相等的实数根，‎ 根据根与系数的关系，方程的两个根的积为，‎ 一个正根，一个负根，‎ 故选：．‎ ‎6．（2019•淮安）若关于的一元二次方程有两个不相等的实数根，则的取值范围是　　‎ A． B． C． D．‎ ‎【解答】解：关于的一元二次方程有两个不相等的实数根，‎ ‎，‎ ‎．‎ 故选：．‎ ‎7．（2019•泰州）方程的两根为、，则等于　　‎ A． B．6 C． D．3‎ ‎【解答】解：由于△，‎ ‎，‎ 故选：．‎ ‎8．（2019•盐城）关于的一元二次方程为实数）根的情况是　　‎ A．有两个不相等的实数根 B．有两个相等的实数根 ‎ C．没有实数根 D．不能确定 ‎【解答】解：‎ 由根的判别式得，△‎ 故有两个不相等的实数根．‎ 故选：．‎ 二．填空题（共21小题）‎ ‎9．（2019•南通）《九章算术》是中国传统数学最重要的著作之一．书中记载：“今有人共买鸡，人出九，盈十一；人出六，不足十六．问人数几何？”意思是：“有若干人共同出钱买鸡，如果每人出九钱，那么多了十一钱；如果每人出六钱，那么少了十六钱．问：共有几个人？”设共有个人共同出钱买鸡，根据题意，可列一元一次方程为　　．‎ ‎【解答】解：设有个人共同买鸡，根据题意得：‎ ‎．‎ 故答案为：．‎ ‎10．（2018•南通）古代名著《算学启蒙》中有一题：良马日行二百四十里．驽马日行一百五十里．驽马先行一十二日，问良马几何追及之．意思是：跑得快的马每天走240里，跑得慢的马每天走150里．慢马先走12天，快马几天可追上慢马？若设快马天可追上慢马，则由题意，可列方程为　　．‎ ‎【解答】解：设快马天可以追上慢马，‎ 据题题意：，‎ 故答案为：‎ ‎11．（2020•南京）已知、满足方程组，则的值为　1　．‎ ‎【解答】解：，‎ ‎①②得：，‎ 则，‎ 故答案为1．‎ ‎12．（2020•无锡）我国古代问题：以绳测井，若将绳三折测之，绳多四尺，若将绳四折测之，绳多一尺，井深几何？这段话的意思是：用绳子量井深，把绳三折来量，井外余绳四尺，把绳四折来量，井外余绳一尺，井深几尺？则该问题的井深是　8　尺．‎ ‎【解答】解：设绳长是尺，井深是尺，依题意有 ‎，‎ 解得，．‎ 故井深是8尺．‎ 故答案为：8．‎ ‎13．（2019•常州）若是关于、的二元一次方程的解，则　1　．‎ ‎【解答】解：把代入二元一次方程中，‎ ‎，解得．‎ 故答案是：1．‎ ‎14．（2019•苏州）若，，则的值为　5　．‎ ‎【解答】解：，，‎ 则，‎ 代入，‎ 解得：，‎ 则，‎ 故．‎ 故答案为：5．‎ ‎15．（2019•宿迁）下面3个天平左盘中“△”“□”分别表示两种质量不同的物体，则第三个天平右盘中砝码的质量为　10　．‎ ‎【解答】解：设“△”的质量为，“□”的质量为，‎ 由题意得：，‎ 解得：，‎ 第三个天平右盘中砝码的质量；‎ 故答案为：10．‎ ‎16．（2018•淮安）若关于、的二元一次方程有一个解是，则　4　．‎ ‎【解答】解：把代入方程得：，‎ 解得：，‎ 故答案为：4．‎ ‎17．（2018•无锡）方程组的解是　　．‎ ‎【解答】解：，‎ ‎②①，得：，‎ 解得：，‎ 将代入①，得：，‎ 解得：，‎ 所以方程组的解为，‎ 故答案为：．‎ ‎18．（2020•南通）1275年，我国南宋数学家杨辉在《田亩比类乘除算法》中提出这样一个问题：直田积八百六十四步，只云阔不及长一十二步．问阔及长各几步．意思是：矩形面积864平方步，宽比长少12步，问宽和长各几步．若设长为步，则可列方程为　　．‎ ‎【解答】解：长为步，宽比长少12步，‎ 宽为步．‎ 依题意，得：．‎ ‎19．（2020•南通）若，是方程的两个实数根，则代数式的值等于　2028　．‎ ‎【解答】解：，是方程的两个实数根，‎ ‎，，即，‎ 则原式 ‎，‎ 故答案为：2028．‎ ‎20．（2020•镇江）一元二次方程的两根分别为　，　．‎ ‎【解答】解：，‎ ‎，‎ 或，‎ 解得，．‎ ‎21．（2020•常州）若关于的方程有一个根是1，则　1　．‎ ‎【解答】解：关于的方程有一个根是1，‎ 把代入方程得：，‎ 解得：，‎ 故答案为：1．‎ ‎22．（2020•泰州）方程的两根为、，则的值为　　．‎ ‎【解答】解：方程的两根为、，‎ ‎．‎ 故答案为：．‎ ‎23．（2020•扬州）方程的根是　，　．‎ ‎【解答】解：，‎ ‎，‎ ‎，．‎ 故答案为：，．‎ ‎24．（2019•镇江）若关于的方程有两个相等的实数根，则实数的值等于　1　．‎ ‎【解答】解：根据题意得△，‎ 解得．‎ 故答案为1．‎ ‎25．（2019•南京）已知是关于的方程的一个根，则　1　．‎ ‎【解答】解：把代入方程得，‎ 解得．‎ 故答案为1．‎ ‎26．（2019•盐城）设、是方程的两个根，则　1　．‎ ‎【解答】解：、是方程的两个根，‎ ‎，，‎ ‎；‎ 故答案为1；‎ ‎27．（2019•连云港）已知关于的一元二次方程有两个相等的实数根，则的值等于　2　．‎ ‎【解答】解：根据题意得：‎ ‎△，‎ 整理得：，‎ ‎，‎ 方程是一元二次方程，‎ ‎，‎ 等式两边同时除以得：，‎ 则，‎ 故答案为：2．‎ ‎28．（2019•扬州）一元二次方程的根是　，　．‎ ‎【解答】解：，‎ ‎，‎ ‎，‎ ‎，，‎ ‎，，‎ 故答案为：，．‎ ‎29．（2019•徐州）方程的解是　　．‎ ‎【解答】解：，‎ 移项得：，‎ 两边直接开平方得：，‎ 故答案为：．‎ 三．解答题（共17小题）‎ ‎30．（2018•镇江）小李读一本名著，星期六读了36页，第二天读了剩余部分的，这两天共读了整本书的，这本名著共有多少页？‎ ‎【解答】解：设这本名著共有页，‎ 根据题意得：，‎ 解得：．‎ 答：这本名著共有216页．‎ ‎31．（2020•镇江）【算一算】‎ 如图①，点、、在数轴上，为的中点，点表示，点表示1，则点表示的数为　5　，长等于　　；‎ ‎【找一找】‎ 如图②，点、、、中的一点是数轴的原点，点、分别表示实数、，是的中点，则点　　是这个数轴的原点；‎ ‎【画一画】‎ 如图③，点、分别表示实数、，在这个数轴上作出表示实数的点（要求：尺规作图，不写作法，保留作图痕迹）；‎ ‎【用一用】‎ 学校设置了若干个测温通道，学生进校都应测量体温，已知每个测温通道每分钟可检测个学生．凌老师提出了这样的问题：假设现在校门口有个学生，每分钟又有个学生到达校门口．如果开放3个通道，那么用4分钟可使校门口的学生全部进校；如果开放4个通道，那么用2分钟可使校门口的学生全部进校．在这些条件下，、、会有怎样的数量关系呢？‎ 爱思考的小华想到了数轴，如图④，他将4分钟内需要进校的人数记作，用点表示；将2分钟内由4个开放通道检测后进校的人数，即校门口减少的人数记作，用点表示．‎ ‎①用圆规在小华画的数轴上分别画出表示、的点、，并写出的实际意义；‎ ‎②写出、的数量关系：　　．‎ ‎【解答】解：（1）【算一算】：记原点为，‎ ‎，‎ ‎，‎ ‎，．‎ 所以点表示的数为5，长等于8．‎ 故答案为：5，8；‎ ‎（2）【找一找】：记原点为，‎ ‎，‎ ‎，‎ ‎，‎ 为原点．‎ 故答案为：．‎ ‎（3）【画一画】：记原点为，‎ 由，‎ 作的中点，‎ 得，‎ 以点为圆心，‎ 长为半径作弧交数轴的正半轴于点，‎ 则点即为所求；‎ ‎（4）【用一用】：在数轴上画出点，；2分钟后，校门口需要进入学校的学生人数为：．‎ 分钟内开放3个通道可使学生全部进校，‎ ‎，即（Ⅰ）；‎ 分钟内开放4个通道可使学生全部进校，‎ ‎，即（Ⅱ）；‎ ‎①以为圆心，长为半径作弧交数轴的正半轴于点，则点即为所求．‎ 作的中点，则，在数轴负半轴上用圆规截取，‎ 则点即为所求．‎ 的实际意义：2分钟后，校门口需要进入学校的学生人数；‎ ‎②方程（Ⅱ）方程（Ⅰ）得：．‎ 故答案为：．‎ ‎32．（2020•徐州）本地某快递公司规定：寄件不超过1千克的部分按起步价计费：寄件超过1千克的部分按千克计费．小丽分别寄快递到上海和北京，收费标准及实际收费如下表：‎ 收费标准 ‎ 目的地 起步价（元 超过1千克的部分（元千克）‎ 上海 北京 实际收费 ‎ 目的地 质量 费用（元 上海 ‎2‎ ‎9‎ 北京 ‎3‎ ‎22‎ 求，的值．‎ ‎【解答】解：依题意，得：，‎ 解得：．‎ 答：的值为7，的值为2．‎ ‎33．（2020•扬州）阅读感悟：‎ 有些关于方程组的问题，欲求的结果不是每一个未知数的值，而是关于未知数的代数式的值，如以下问题：‎ 已知实数、满足①，②，求和的值．‎ 本题常规思路是将①②两式联立组成方程组，解得、的值再代入欲求值的代数式得到答案，常规思路运算量比较大．其实，仔细观察两个方程未知数的系数之间的关系，本题还可以通过适当变形整体求得代数式的值，如由①②可得，由①②可得．这样的解题思想就是通常所说的“整体思想”．‎ 解决问题：‎ ‎（1）已知二元一次方程组则　　，　　；‎ ‎（2）某班级组织活动购买小奖品，买20支铅笔、3块橡皮、2本日记本共需32元，买39支铅笔、5块橡皮、3本日记本共需58元，则购买5支铅笔、5块橡皮、5本日记本共需多少元？‎ ‎（3）对于实数、，定义新运算：，其中、、是常数，等式右边是通常的加法和乘法运算．已知，，那么　　．‎ ‎【解答】解：（1）．‎ 由①②可得：，‎ 由①②可得：．‎ 故答案为：；5．‎ ‎（2）设铅笔的单价为元，橡皮的单价为元，日记本的单价为元，‎ 依题意，得：，‎ 由①②可得，‎ ‎．‎ 答：购买5支铅笔、5块橡皮、5本日记本共需30元．‎ ‎（3）依题意，得：，‎ 由①②可得：，‎ 即．‎ 故答案为：．‎ ‎34．（2020•淮安）某停车场的收费标准如下：中型汽车的停车费为15元辆，小型汽车的停车费为8元辆．现在停车场内停有30辆中、小型汽车，这些车共缴纳停车费324元，求中、小型汽车各有多少辆？‎ ‎【解答】解：设中型汽车有辆，小型汽车有辆，‎ 依题意，得：，‎ 解得：．‎ 答：中型汽车有12辆，小型汽车有18辆．‎ ‎35．（2020•连云港）解方程组 ‎【解答】解：‎ 把②代入①，得，‎ 解得．‎ 把代入②，得．‎ 原方程组的解为．‎ ‎36．（2019•淮安）某公司用火车和汽车运输两批物资，具体运输情况如下表所示：‎ 所用火车车皮数量（节 所用汽车数量（辆 运输物资总量（吨 第一批 ‎2‎ ‎5‎ ‎130‎ 第二批 ‎4‎ ‎3‎ ‎218‎ 试问每节火车车皮和每辆汽车平均各装物资多少吨？‎ ‎【解答】解：设每节火车车皮装物资吨，每辆汽车装物资吨，‎ 根据题意，得，‎ ‎，‎ 每节火车车皮装物资50吨，每辆汽车装物资6吨；‎ ‎37．（2019•盐城）体育器材室有、两种型号的实心球，1只型球与1只型球的质量共7千克，3只型球与1只型球的质量共13千克．‎ ‎（1）每只型球、型球的质量分别是多少千克？‎ ‎（2）现有型球、型球的质量共17千克，则型球、型球各有多少只？‎ ‎【解答】解：（1）设每只型球、型球的质量分别是千克、千克，根据题意可得：‎ ‎，‎ 解得：，‎ 答：每只型球的质量是3千克、型球的质量是4千克；‎ ‎（2）现有型球、型球的质量共17千克，‎ 设型球1个，设型球个，则，‎ 解得：（不合题意舍去），‎ 设型球2个，设型球个，则，‎ 解得：（不合题意舍去），‎ 设型球3个，设型球个，则，‎ 解得：，‎ 设型球4个，设型球个，则，‎ 解得：（不合题意舍去），‎ 设型球5个，设型球个，则，‎ 解得：（不合题意舍去），‎ 综上所述：型球、型球各有3只、2只．‎ ‎38．（2018•扬州）对于任意实数，，定义关于“”的一种运算如下：．例如．‎ ‎（1）求的值；‎ ‎（2）若，且，求的值．‎ ‎【解答】解：（1），‎ ‎；‎ ‎（2），且，‎ ‎，‎ 两式相加，可得 ‎，‎ ‎．‎ ‎39．（2018•宿迁）解方程组：．‎ ‎【解答】解：，‎ ‎①②得：‎ ‎，‎ 解得：，‎ 故，‎ 解得：，‎ 故方程组的解为：．‎ ‎40．（2020•徐州）（1）解方程：；‎ ‎（2）解不等式组：．‎ ‎【解答】解：（1），‎ ‎，‎ 或，‎ 解得：，；‎ ‎（2）‎ 解不等式①，得．‎ 解不等式②，得．‎ 则原不等式的解集为：．‎ ‎41．（2020•无锡）解方程：‎ ‎（1）；‎ ‎（2）．‎ ‎【解答】解：（1），，，‎ ‎△，‎ ‎，‎ ‎，；‎ ‎（2），‎ 解①得，，‎ 解②得，，‎ 所以不等式组的解集为．‎ ‎42．（2020•南京）解方程：．‎ ‎【解答】解：原方程可以变形为 ‎，‎ ‎，．‎ ‎43．（2019•无锡）（1）解方程：；‎ ‎（2）解不等式组：．‎ ‎【解答】解：（1），，，‎ ‎△，‎ 则；‎ ‎（2）解不等式，得：，‎ 解不等式，得：，‎ 则不等式组的解集为．‎ ‎44．（2019•徐州）如图，有一块矩形硬纸板，长，宽．在其四角各剪去一个同样的正方形，然后将四周突出部分折起，可制成一个无盖长方体盒子．当剪去正方形的边长取何值时，所得长方体盒子的侧面积为？‎ ‎【解答】解：设剪去正方形的边长为，则做成无盖长方体盒子的底面长为，宽为，高为，‎ 依题意，得：，‎ 整理，得：，‎ 解得：，．‎ 当时，，不合题意，舍去．‎ 答：当剪去正方形的边长为时，所得长方体盒子的侧面积为．‎ ‎45．（2019•南京）某地计划对矩形广场进行扩建改造．如图，原广场长，宽，要求扩充后的矩形广场长与宽的比为．扩充区域的扩建费用每平方米30元，扩建后在原广场和扩充区域都铺设地砖，铺设地砖费用每平方米100元．如果计划总费用642000元，扩充后广场的长和宽应分别是多少米？‎ ‎【解答】解：设扩充后广场的长为，宽为，‎ 依题意得：‎ 解得，（舍去）．‎ 所以，，‎ 答：扩充后广场的长为，宽为．‎ ‎46．（2019•无锡）解方程：‎ ‎（1）；‎ ‎（2）．‎ ‎【解答】解：（1），，，‎ ‎△，‎ 则，‎ ‎；‎ ‎（2）两边都乘以，得：，‎ ‎，‎ ‎，‎ ‎，‎ ‎，‎ 经检验是方程的解．‎