2020年秋九年级数学上册 第3章圆的基本性质 11页

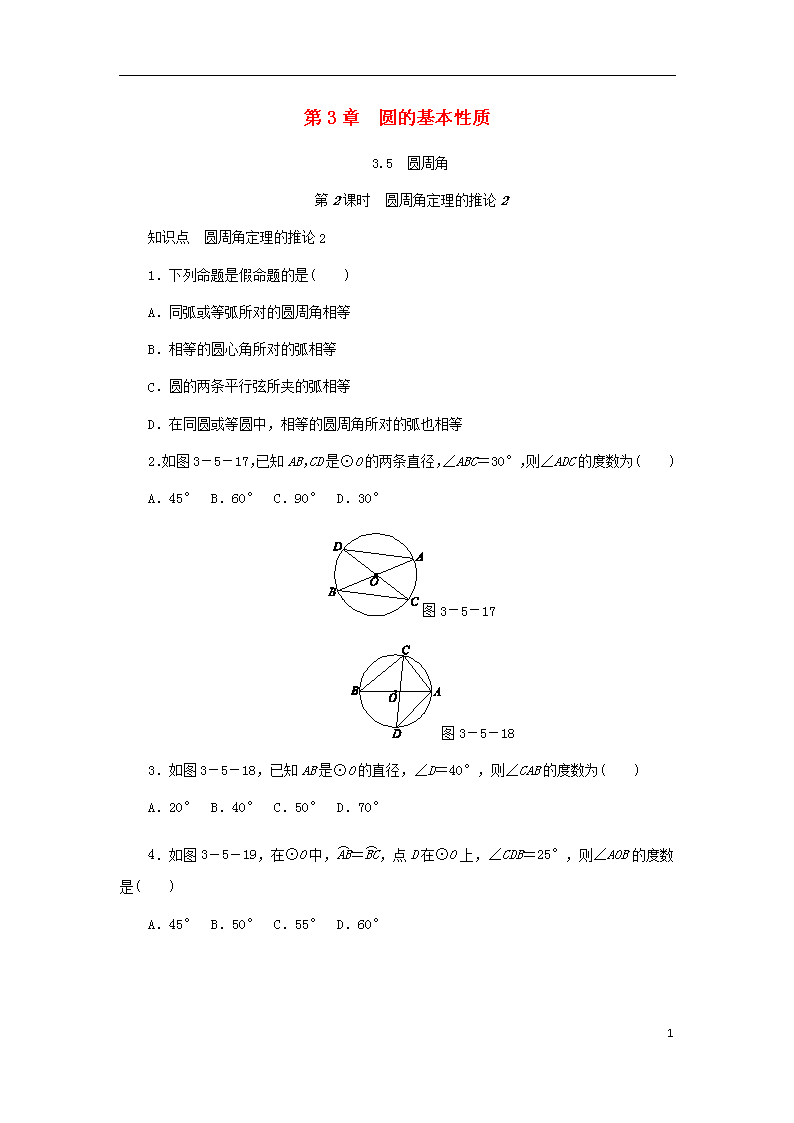
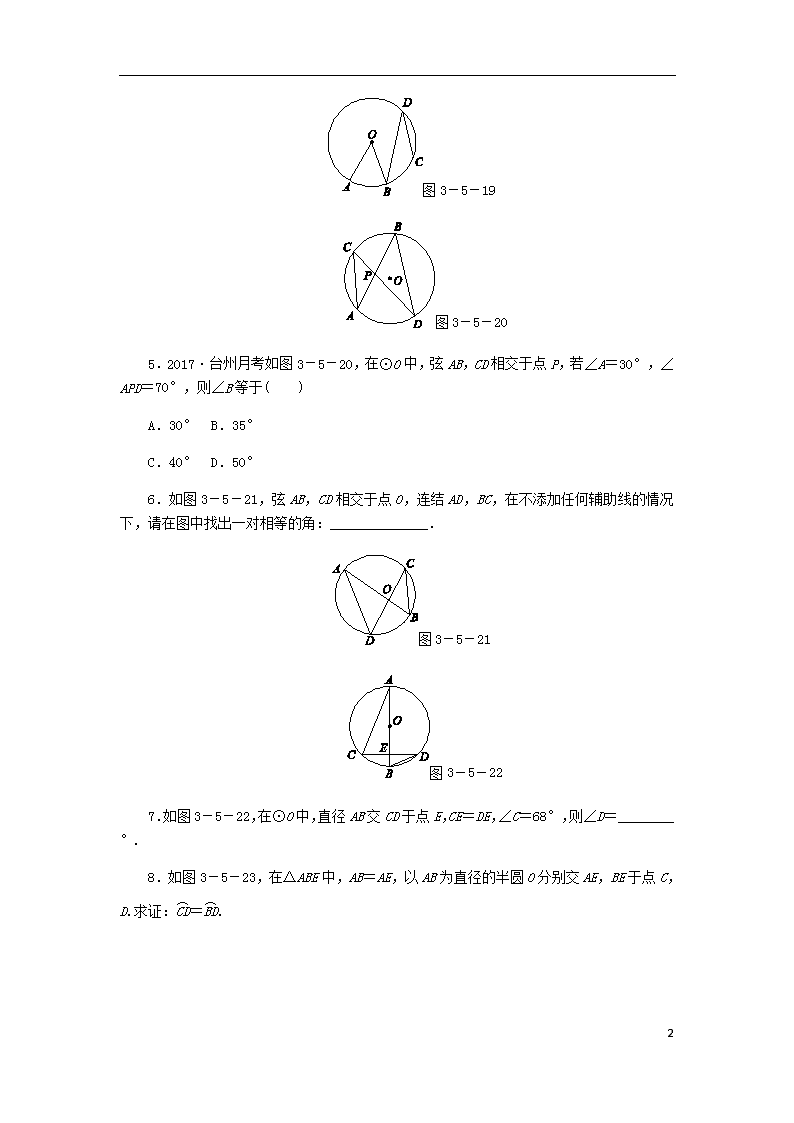
第3章　圆的基本性质 ‎3.5　圆周角 第2课时　圆周角定理的推论2‎ 知识点　圆周角定理的推论2‎ ‎1．下列命题是假命题的是(　　)‎ A．同弧或等弧所对的圆周角相等 B．相等的圆心角所对的弧相等 C．圆的两条平行弦所夹的弧相等 D．在同圆或等圆中，相等的圆周角所对的弧也相等 ‎2．如图3－5－17，已知AB，CD是⊙O的两条直径，∠ABC＝30°，则∠ADC的度数为(　　)‎ A．45° B．60° C．90° D．30°‎ 图3－5－17‎ ‎　　　图3－5－18‎ ‎3．如图3－5－18，已知AB是⊙O的直径，∠D＝40°，则∠CAB的度数为(　　)‎ A．20° B．40° C．50° D．70°‎ ‎4．如图3－5－19，在⊙O中，＝，点D在⊙O上，∠CDB＝25°，则∠AOB的度数是(　　)‎ A．45° B．50° C．55° D．60°‎ 11‎ 图3－5－19‎ ‎　　图3－5－20‎ ‎5．2017·台州月考如图3－5－20，在⊙O中，弦AB，CD相交于点P，若∠A＝30°，∠APD＝70°，则∠B等于(　　)‎ A．30° B．35°‎ C．40° D．50°‎ ‎6．如图3－5－21，弦AB，CD相交于点O，连结AD，BC，在不添加任何辅助线的情况下，请在图中找出一对相等的角：______________．‎ 图3－5－21‎ ‎　　图3－5－22‎ ‎7．如图3－5－22，在⊙O中，直径AB交CD于点E，CE＝DE，∠C＝68°，则∠D＝________°.‎ ‎8．如图3－5－23，在△ABE中，AB＝AE，以AB为直径的半圆O分别交AE，BE于点C，D.求证：＝.‎ 11‎ 图3－5－23‎ ‎9．2017·济南如图3－5－24，AB是⊙O的直径，∠ACD＝25°，求∠BAD的度数．‎ 图3－5－24‎ ‎10．2017·嘉兴十校联合模拟如图3－5－25，AB是⊙O的直径，CD是⊙O的弦，若∠BAD＝48°，则∠DCA的大小为(　　)‎ A．48° B．42° C．45° D．24°‎ 11‎ 图3－5－25‎ ‎　　图3－5－26‎ ‎11．如图3－5－26，点A，B，C，D都在⊙O上，的度数为84°，则∠ABD＋∠CAO＝________°.‎ ‎12．如图3－5－27，四边形ABCD的四个顶点均在⊙O上，点E在对角线AC上，EC＝BC＝DC.‎ ‎(1)若∠CBD＝39°，求∠BAD的度数；‎ ‎(2)求证：∠1＝∠2.‎ 图3－5－27‎ ‎13．课本例3变式如图3－5－28，在“世界杯”足球比赛中，甲带球向对方球门PQ进攻．当他带球冲到A点时，同伴乙已经助攻冲到B点．有两种射门方式：第一种是甲直接射门；第二种是甲将球传给乙，由乙射门．仅从射门角度考虑，选择哪种射门方式较好？为什么？‎ 11‎ 图3－5－28‎ ‎14．如图3－5－29，已知BC是⊙O的一条弦，A是⊙O的优弧BAC上的一个动点(点A与点B，C不重合)，∠BAC的平分线AP交⊙O于点P，∠ABC的平分线BE交AP于点E，连结BP.‎ ‎(1)求证：P为的中点；‎ ‎(2)PE的长度是否会随点A的运动而变化？请说明理由．‎ 图3－5－29‎ ‎15．创新学习如图3－5－30，⊙O的半径为1，A，P，B，C是⊙O上的四个点，∠APC＝∠CPB＝60°.‎ ‎(1)判断△ABC的形状：____________；‎ ‎(2)试探究线段PA，PB，PC之间的数量关系，并证明你的结论；‎ 11‎ ‎(3)当点P位于的什么位置时，四边形APBC的面积最大？并求出最大面积．‎ 图3－5－30‎ 11‎ 详解详析 ‎1．B ‎2．D　[解析] ∵∠D与∠B所对的弧相同，‎ ‎∴∠D＝∠B＝30°.‎ ‎3．C　[解析] ∵∠D＝40°，∴∠B＝∠D＝40°.∵AB是⊙O的直径，∴∠ACB＝90°，∴∠CAB＝90°－40°＝50°.‎ ‎4．B　[解析] 在同一个圆中，等弧所对的圆心角是圆周角的2倍，故选B.‎ ‎5．C　[解析] ∵∠APD是△APC的外角，‎ ‎∴∠APD＝∠C＋∠A.‎ ‎∵∠A＝30°，∠APD＝70°，‎ ‎∴∠C＝∠APD－∠A＝40°，‎ ‎∴∠B＝∠C＝40°.‎ 故选C.‎ ‎6．答案不唯一，如∠A＝∠C ‎7．22‎ ‎8．证明：∵AB是⊙O的直径，∴∠ADB＝90°，‎ 即AD⊥BE.‎ 又∵AB＝AE，∴∠BAD＝∠CAD，‎ ‎∴＝.‎ ‎9．解：∵AB为⊙O的直径，‎ ‎∴∠ADB＝90°.‎ ‎∵∠ACD＝25°，∴∠B＝25°，‎ ‎∴∠BAD＝90°－∠B＝65°.‎ 11‎ ‎10．B　[解析] 连结BD，如图所示．‎ ‎∵AB是⊙O的直径，‎ ‎∴∠ADB＝90°，‎ ‎∴∠ABD＝90°－∠BAD＝42°，‎ ‎∴∠DCA＝∠ABD＝42°.‎ 故选B.‎ ‎11．48　[解析] 在等腰三角形OAC和等腰三角形OCD中，根据等腰三角形的两个底角相等的性质求得∠OCA＝∠OAC，∠OCD＝∠ODC，所以由三角形的内角和定理求得∠OCD＝48°；由圆周角定理的推论得∠ABD＝∠ACD，进而求得∠ABD＋∠CAO＝∠ACD＋∠OCA＝∠OCD＝48°.‎ ‎12．(1)∵BC＝DC，‎ ‎∴∠CBD＝∠CDB＝39°.‎ ‎∵∠BAC＝∠CDB＝39°，∠CAD＝∠CBD＝39°，‎ ‎∴∠BAD＝∠BAC＋∠CAD＝39°＋39°＝78°.‎ ‎(2)证明：∵EC＝BC，‎ ‎∴∠CEB＝∠CBE，‎ 而∠CEB＝∠2＋∠BAE，∠CBE＝∠1＋∠CBD，‎ ‎∴∠2＋∠BAE＝∠1＋∠CBD.‎ ‎∵∠BAE＝∠CBD，∴∠1＝∠2.‎ ‎13．解：选择第二种射门方式较好．‎ 理由：设AP与圆的交点是C，连结CQ，‎ 则∠PCQ＞∠A.‎ 11‎ 由圆周角定理知∠PCQ＝∠B，‎ 所以∠B＞∠A，‎ 所以选择第二种射门方式较好．‎ ‎14：(1)证明：∵AP平分∠BAC，‎ ‎∴∠BAP＝∠CAP，‎ ‎∴＝，即P为的中点．‎ ‎(2)PE的长度不会随点A的运动而变化．‎ 理由：∵∠BAP＝∠CAP，∠CAP＝∠CBP，‎ ‎∴∠BAP＝∠CBP.‎ ‎∵BE平分∠ABC，‎ ‎∴∠ABE＝∠CBE，‎ ‎∴∠ABE＋∠BAE＝∠CBE＋∠CBP，‎ ‎∴∠BEP＝∠EBP，‎ ‎∴PE＝PB.‎ ‎∵P为的中点，即PB为定长，‎ ‎∴PE的长度为定值，即PE的长度不会随点A的运动而变化．‎ ‎15．解：(1)等边三角形 ‎(2)PA＋PB＝PC.‎ 11‎ 证明：如图①，在PC上截取PD＝‎ PA，连结AD.‎ ‎∵∠APC＝60°，‎ ‎∴△PAD是等边三角形，‎ ‎∴PA＝AD, ∠PAD＝60°.‎ 又∵∠BAC＝60°，∴∠PAB＝∠DAC.‎ 又∵AB＝AC，‎ ‎∴△PAB≌△DAC，∴PB＝DC.‎ ‎∵PD＋DC＝PC，∴PA＋PB＝PC.‎ ‎(3)当点P为的中点时，四边形APBC的面积最大．‎ 如图②，过点P作PE⊥AB，垂足为E，过点C作CF⊥AB，垂足为F.‎ ‎∵S△PAB＝AB·PE, S△ABC＝AB·CF，‎ ‎∴S四边形APBC＝S△PAB＋S△ABC＝AB(PE＋CF). ‎ 当点P为的中点时，PE＋CF＝PC，PC为⊙O的直径，‎ 此时四边形APBC的面积最大．‎ ‎∵⊙O的半径为1，‎ 11‎ ‎∴其内接正三角形的边长AB＝，‎ ‎∴S四边形APBC＝×2×＝.‎ 11‎