全国中学生物理竞赛课件24：几何光学问题集成 39页

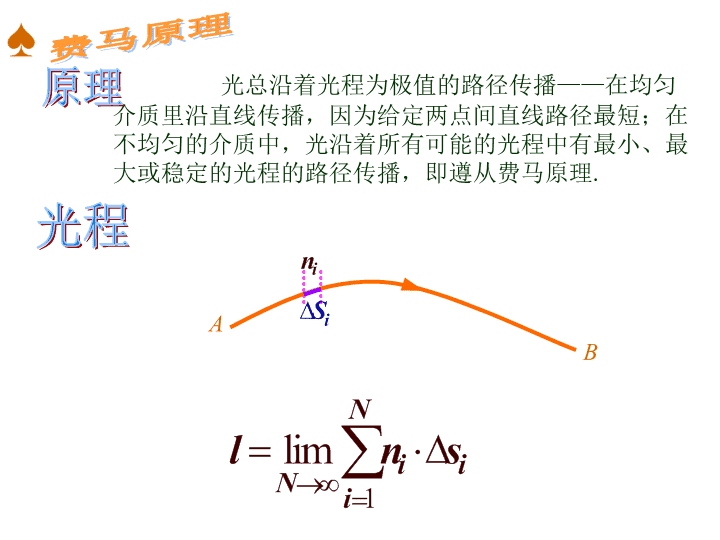
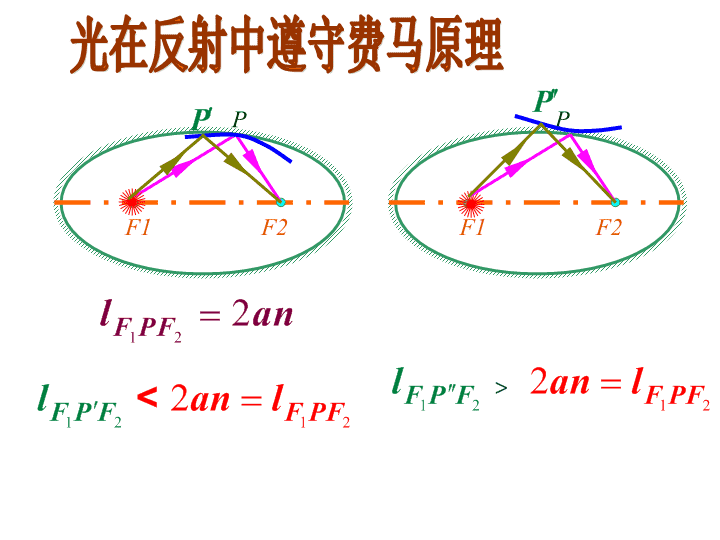
光总沿着光程为极值的路径传播——在均匀介质里 沿直线传播，因为给定两点间直线路径最短；在不均匀 的介质中，光沿着所有可能的光程中有最小、最大或稳 定的光程的路径传播，即遵从费马原理. 1 lim N i iN i l n s    ♠ in iSA B F1 F2 PP 1 2 2F PFl an 2 11 2 2F P F F PFa ll n<  F1 F2 PP 2 21 1 2P F F PFF an ll >  n1 n2 N O r i aa 1h x 2h y A B 1 2AOBl n AO n OB    2 2 2 2 1 1 2 2n x h n y h       22 2 2 1 1 2 2n x h n a x h       光程有最值应满足      2 2 22 2 2 2 2 1 1 2 2 1 1 2 2 0 lim 0x n x x h n a x x h n x h n a x h x                    1 22 2 2 2 1 2 x yn n x h y h    1 2sin sinn i n r即    0 0 02l n h R h     依据费马原理求解:  0 0 02 na h R ha          0 0 0 0 n nh R h R Ca a          由基本不等式:  0 0 0 0 01 2 n h R h ha n Ra            当 , = 时光程有最大值 即在 01 2 n Ra     处存在光的圆折射波道 某行星上大气的折射率随着行星表面的高 度h按照n＝n0－ah的规律而减小，行星的半径为R，行星 表面某一高度h0处有光波道，它始终在恒定高度，光线沿 光波道环绕行星传播，试求高度h0． 查阅 物像公 式 依据惠更斯原理求解: M N h0 h O 0 h h h c c h n hn  由 0 0 0 0 0 0( ) ( ) c c n ah n a R h R h h h h               0 0 0 0 0 0n ah R h n ah a h R h h                0 0 0n ah h a h R h     0 0 1 2 nh Ra     R 返回 光源形成的单心光束的顶点 ♠ 实物点 虚物点 被光具作用(折射、反射）后的单心光束的会聚 点或发散点称作实像点或虚像点 y P y O1 x Q h i i 2  A FC O B S S OP u OQ v        1 2 2 2 2 SO Sl u x y h v x y h         根据费马原理可以推论，任 一发光点所发光束经球面反 射或折射后能成像于一点的 条件是，从物点到达像点的 所有光线的光程都相等 对近轴光线             2 2 2 2 2 21 1y h y hu x v x u x v x                                  2 2 2 2 y h y hu x v xu x v x          2 2 y h u   2 2 y h v   2x h   2 hh r   2 2 2 1 1 2 2 2 2 y y y y hl u v hu v u v u v r                   1 1 1 u v f   y vk y u   S x 1S S S2 x 根据近轴光线平面折射规律:  2 1SS n x  根据球面镜物象公式:   1 1 1 1 40 2 40 10n x x      24.2cmx  某观察者通过一块薄玻璃板去看在凸面镜 中他自己眼睛的像．他移动着玻璃板，使得在玻璃板中与 在凸面镜中所看到的他眼睛的像重合在一起．若凸面镜的 焦距为10 cm，眼睛与凸面镜顶点的距离为40 cm，问玻璃 板距观察者眼睛的距离为多少？ A B P P 2  2  2  　　　　　 圆锥面的内表面镀上反射层，构成圆锥面镜．在 圆锥形内沿轴拉紧一根细丝．要使细丝发出的光线在圆锥内面上反 射不多于一次，圆锥形最小的展开角α=____________． P P3 1802   若 一次反射光无入射点 120  则 120 2  2 2  100m 2 3 400m m   　　　　　 小路灯L发出的光束在离灯R0＝100 m处会聚成小光斑 A．在光传播的路径上放两个正方形平面镜，如图．两镜面的交线到 灯的距离r＝70 m，并且垂直穿过光束轴．两面镜互相垂直，其中一 个平面镜与光束轴交成角α＝30°，则现在光束将会聚在离灯 __________m处． L发出的光为会聚光束，A为虚物点 轴以上部分光束经平面镜OM反射仍为会聚光束，顶点 在A1，A1与A关于OM对称 同理，L发出的轴以下部分光束先经平面镜ON反射、再 经平面镜OM反射亦不改变会聚性，并由对称性知会聚于A3 向A1会聚的这束光射向平面镜ON并被二次反射，反射光束 会聚于A3，相当于虚物A1通过ON成实像，A3与A1关于ON对 称，由于OM与ON垂直，易知A3在L发出的光束轴上且OA3= OA； 则两垂直平面镜将令灯 发出的光束会聚于离灯 虚物 L A A2 N M O A1 A3 40 SS 与S  S  两像情况完全相同,关于平面镜对称 　　　　　 由点光源S发出的近轴光线经透明球形成像，像到透 明球的距离为b，如图所示．如果沿垂直于水平轴将球分成两半，左 边一半的平面上镀银，那么像的位置在__________，与球的距离为 ____________． 左半平面镀银成平面镜，通过左球面 的折射光线通过平面镜反射不改变光 束敛散性只是再次由左球面折射而已 b 左侧 b 底 水醇界面 醇表面 h2 h1 H y S 对水醇界面 对醇气界面 ny hn 2 1 1  1.36 3 21.33 cm1.36    y hH n 2 2  3.7cm 　　　　　 深度为3 cm的水面上（n1=1.33）漂浮着2 cm厚的醇 （n2=1.36）层，则水底距醇表面的像视深度为___________． 3.7cm  1 不经反射，入射光能射到感光面 上，入射光与轴所成最大角如图  2 经一次反射而能入射光面上， 入射光与轴所成最大角增大 m 以最大角度入射的光 线延长后应恰与接受器表 面相切，如图   max 2     d L r sin 2 2   而 r L r L d  2sin 1 sin 0.52     max 3630 6     　　　　　 如图所示，两块平面镜宽度均为L＝5 cm ，相交 成角α＝12°，构成光通道．两镜的右端相距为d＝2 cm，左端靠在光 接收器的圆柱形的感光面上．试问入射光线与光通道的轴成的最大 角度为多少，才能射到光接收器上？ y xO 光穿过几个互相平行的、折 射率不同的介质区时 有 0 1 1sin sin sini in n r n r    y xO n1 ni n2n3 r i ri+1y r i O点光沿x方向,则第i层入射角ri满足 0 0sin sin90i i i n nr n n   由图示几何关系得 0sin 1i i ny R R r R n         0( ) Rn y nR y   0 1, 2.5mn n   1 190 sin 2.5m   66.4  　　　　　 如图所示，介质在一定区域x＞0、y＞0内的折射率 随着y的变化而连续变化．一束细光束沿x方向垂直入射到介质表面， 并沿着一个半径为R的圆弧路径穿过介质，求折射率n随y变化的规 律．如果y=0时折射率n0=1，已知的材料中最大折射率（金刚石折射 率）不超过2.5，圆弧所对应的圆心角最大可能达多少？ 折射光具之三棱镜 对光路的作用 A B C O O δ i r r i D E 顶角 偏向角δ 反映三棱镜改变光传播方向的程 度!    i r i r      r r A  i i A    min 2i A   i i 　　　　　 通常用阿贝数 来表示光学材料的色散 特性，其中nD 、nC、nF 分别表示材料对单色光D及单色光C及F的 折射率．一束白光照射到一顶角A=60°，冕牌玻璃（n=1.500， n=1.495，）制的棱镜上，使单色光D在棱镜中的传播方向垂直于角A 的平分面．求从棱镜射出的单色光C和F之间的夹角．    1 /D F Cn n n    解答 A i r r i  本题比较三棱镜对C、D、F三 种色光改变传播方向的程度！ 单色光D对称进出三棱镜，光路如示 单色光D通过三棱镜偏向角为 2D i A   1 1sin sin sin 0.7502D Ai n   单色光C通过三棱镜偏向角小于D C Ci i A    单色光F通过三棱镜偏向角大于D F Fi i A    F C F Ci i     则 其中   sin sin sinsin F F CC i in rA r   由 = 得 49 24Fi      sin sin sinsin C C CC i in rA r    由 得 48 16Ci    1.08F C    走“光对称进出三棱镜”时的路径时间最 短，即沿图答中折线APQB，其中PQ∥AB， 借助光折射模型： P Q r D CA h Bl sin 2sin 2 i v vr   2 r  由几何关系 cos hAP QB i    2 22 tan sin 2PQ l h h i    则最短时间为  l h h ih h l ht hv i v vv v      2 2 2 2 2 2 4 tan sin 2sin2 22 24 sincos 21 4sin 1 4sin2 2                2 20, tan ,PQ l h h i  若 即 2lt v  2 2 24sin 2 1 4sin2 2l h h v      　　　　　 如图．湖湾成顶角为α的楔形，岸上住有一个渔人： 他的房子在A点，从A点到他离湖最近的C点之距离为 h，而到湖湾的 一头，即到D点之距离为．湖对岸B点处有渔人好友的房子，点B位 置与A点相对湖岸对称．渔人拥有一只小船，他可以速度沿岸步行或 以速度v/2乘船在湖中划行，他从自己家出发到好友家里去．求他需 要的最短时间．  i 2 2 2 2 2 4sin 2 , 1 4sin 2 l h h      从BC看到压在玻璃棱镜下的文字， 需有进入棱镜的光从AC面折射到报纸， 经由纸面反射回棱镜再出射到观察者视 场中！若投射到AC面某部分的光发生 了全反射，其下面文字就看不见了； 　　　　　 如图,等腰直角玻璃镜的底面AC和侧面BC是光滑的,而侧 面AB是毛糙的，棱镜的底面放在报纸上,一位观察者从光滑面BC 看 去,只看见报纸上一篇文章的一部分，这可见部分与应见部分之比为 k=0.95(按面积),求玻璃的折射率．  1 0.95a AC ll    由几何关系，在三角形ADB中有     sin 452sin 90 l a    tan 0.9  n  1sin  21 0.9 1.50.9 n   A B C a D 设全反射临界角为α,从BC面最上 端进入的光线BD恰发生全反射，则 AD间没有射向报纸的光线，是看不 到文字的区域，即有  　　　　　 假定你站在水平的大沙漠上．在远处，你会看见好似 水面的东西，当你靠近“水面”时，它会同时后退，并保持你同它 的距离不变，试解释这一现象．假定你的两眼离地面1.6m，且你同 “水面”的距离保持为250 m，试计算地表温度．空气在15℃，一个 大气压下的折射率为1.0002760，假定在距地面1 m以上空气温度恒为 30℃，大气压强为0.1013 MPa．折射率用n表示，并假定(n-1)同空气 密度成正比． 由于(n-1)∝ρ，温度T越 高，空气密度越小，折射率也 越小，大沙漠地表温度较高， 高处景物（例如白云）的光自 上向下行进，连续从光密介质 向光疏介质折射，在地面附近 发生全反射，反射光进入人眼 的结果是看到了景物的虚像， 形似水面 沙漠蜃景 解答 n0,T0 n30,T30 1m 1.6m 250m 根据克拉珀龙方 程，压强一定时有  , 1T C n   而 ， 30 0sin sin90n n   0 30 0 1 303 1 n n T   由   11n T  则 2 2 250sin 250 1.6    其中 0 2 2 288 0.0002760 288 2500.0002760 1 1303 250 1.6 T          329 K    30 15 2881 1 303n n  而  ⑴若要求此光束进入长方体能射至AD面 上，折射光至少能射至D点： D A B C r P m 1tan 2 sin sin r nr       则 1 min sin 5 n  sin sin 5 nn r   ⑵若要求此光束能在AD面上全反射，应满足   21 sin 1sin 90 1r n n n          2 1 sinn   5 n 2 1 , 5 5 2 nn n   , 5 51n n  5 52 n  ⑶如示： 　　　　　 图中的矩形ABCD代表一个折射率为n的透明长方体， 其四周介质的折射率为1，一束单色细光束以角θ入射至AB面上的P 点， ．不考虑在长方体内的二次及二次以上的多次折射， 试解下面三个问题: ⑴若要求此光束进入长方体能射至AD面上，角θ 的最小值θmin应为多大？⑵若要求此光束能在AD面上全反射，角θ应 在什么范围内？长方体的折射率n应在什么范围内？⑶画出角θ小于 上问中许可的最小角及大于上问中许可的最大角时的光路图. 1 2AP AD 2fR r 若将此透镜的平面镀银， 其作用要等同于一个焦距 是30 cm 的凹面镜，应使 主轴上距球面顶点2f的物 点发出的光进入球内后与 镀银平面垂直地入射，则 反射后光反向沿原路径到 达主轴上物点处，即等效 于凹面镜过曲率中心的光 线反射后仍过曲率中心  2 tan tanf i r R r    3 2 i r  　　　　　 有一薄凸透镜，凸面曲率半径R=30 cm，如图所 示．已知在利用近轴光线成像时：⑴若将此透镜的平面镀银，其作 用等同于一个焦距是30 cm 的凹面镜 ；⑵若将此透镜的凸面镀银， 其作用也等同于一个凹面镜．求在⑵情况下的等效凹面镜的焦距． i 由图示几何关系得  2 f i r R r   对近轴光线，由几何关系得 续解 x i R 若将此透镜的凸面镀银，其作用也要 等同于一个凹面镜，应使进入镜中的 光沿凸面的径向射至镀银球面，则反 射后光沿原路径返回，设等效凹面镜 曲率半径为x 由图示几何关系得 r 2x f  tan tanx i R r   10cmf   2 f i R r   对近轴光线，由几何关系得 3 2 i r 而 查阅 　　　　　 有一薄透镜如图示，S1面是旋转椭球面（椭圆绕长轴 旋转而成的曲面），其焦点为F1和F2；S2面是球面，其球心C与F2重 合．已知此透镜放在空气中时能使从无穷远处位于椭球长轴的物点 射来的全部入射光线（不限于傍轴光线）会聚于一个像点上，椭圆 的偏心率为e．⑴求此透镜材料的折射率n（要论证）；⑵如果将此 透镜置于折射率为n′的介质中，并能达到上述的同样的要求，椭圆 应满足什么条件？ 1 2 1 1 1 2 2 F FO F O F a e    符合要求的透镜形成光路如示 S1 S2 F2F1 C O1i r 由几何关系     1 2 1 1 1 2 sin 2 sin sin F F O F O F r i r i r    sin sin 1i r ne   透镜置于折射率为n1的介质中时 1sin 1 sin ni r e n   1ne n  N N C E A B ①② ③ ④ ⑤ ⑥ O F K G 　　　　　 如图表示一条光线经过薄会聚透镜折射的光路ABC和 透镜的后焦点F．试用圆规和直尺，作出透镜所在位置和它的主光 轴． ①连接B、F两点； ②以BF为直径作圆； ③延长入射线AB； ④用有刻度的直尺零刻线对准点F，以F 为轴转动直 尺，当FK=GE时，作线段EF； ⑤过F点作EF的垂线为主轴， 与圆交于O即为光心； ⑥OB为透镜所在位置 ∵BG⊥EF Rt BEG Rt OKF    则OK∥AB为副光轴 EF为焦平面 AB经透镜折射后的光线过副焦点K，即为BC L O DE G C AB1 6A B B A v v u u    根据题意 2 3B C C B v v u u    1 1 1 A Af u v   1 1 1 C Cf u v   1 1 1 B Bf u v   B B v u   BD放大率为 1 2 1 2 2     根据公式 2 　　　　　 利用薄凸透镜得到三齿的像，如图．三齿ABCEDG 的底边AC位于主光轴上，AB=BC．AB部分成像放大率β1=6，而BC 部分的放大率β2=3 ，试求BD部分成像的放大率． S1 S2 物直接经透镜成放大虚像 物经平面镜的反射光再经透镜成放大实像 设前一像之像距v1，后一像之像距v2，蜡烛距透镜u，则 1 1 1 1 f u v   2 1 1 1 2f L u v   1 2 2 v v u L u  两像放大率为 f L 　　　　　 在不透光的箱内直立着一根蜡烛，箱的后壁是平面 镜，前壁嵌有透镜，如图，箱长为L，在这光具组中观察到蜡烛火焰 的两个像，并且像的大小相等．试求透镜的焦距． 物、像位置重合是平面镜使光路可逆而成！ L O L O 由透镜成像公式： 1 1 1 f f l L   1 1 1 9 4f f   3cmf  　　　　　 凸透镜后面距离L=4 cm（大于焦距）处放置一块垂直 于主光轴的平面镜，透镜前面垂直于主光轴放一页方格纸，如 图．当这页纸相对透镜移动两个位置时（这两个位置相距=9 cm）， 纸上均得到其方格的像．试求凸透镜的焦距． F2 L1 L2 F1 对L1成S的等大倒立实像: 1 1 1 1 1 1 2f f v   1 20cmv  对L2成S1的缩小倒立实像: 2 2 1 1 1 2f d f v   2 12.5cmv  S S2 L3 S1 　　　　　 如图所示的薄透镜系统中，透镜L1和L2的焦距 f1=f2=10 cm，两透镜的间距为70 cm，物在L1的前方20 cm处，试求 最后像的位置、大小与正倒；为提高光能利用率（增加系统的聚光 能力以增加像亮度），可增加第三个会聚透镜L3，为了使最后像的 位置仍保持不变，试问L3应放在何处？试借助特殊光线用作图法解 释L3能提高聚光能力的原因。 y O1 -s n1 n2 s y x h P P i C O A B r 根据费马原理可以推论，任一发光点所发光束经球面折射后 能成像于一点的条件是，从物点到达像点的所有光线的光程 都相等        1 2 2 2 2 1 2PO Pl n s x y h n s x y h                        2 2 2 2 1 2 21 1y h y hn s x s x s x s x                                     2 2 1 1 2 22 2 y h y hn s x n n s x ns x s x              2 2 y h s    2 2 y h s    2 1 2 1n n n n s s R  1 2 0y yn ns s   2 2 2 1 2 1 2 1 2 1 2 1 2 2 2 2 n y n y n y n y n n n nhl n s n s hs s s s s s R R                         2 2 2 1 n Rf n n   1 1 1 2 n Rf n n   2 2 n f 1 1 n f   1 2 1f f s s   1 2 ny s y n s      d - R2 s-s n1 n2 s PO O A B n P R1 P 对球面AOB运用球面折射公 式: 1 1 1 n n nn s s R   对球面AO′B运用球面折射公式: 2 2 2 n n nn s s d R     薄透镜d→0 2 1 1 2 1 2 n n n n n n s s R R     物方焦距 1 2 1 1 1 1 2 1 n n n n f n R n R     像方焦距 1 2 2 2 1 2 2 1 n n n n f n R n R    1 2 1f f s s   h n对球面所成第1个像运用高 斯公式: 1 2 12 f f R s   其中 1 1 21 1 5f R R.    2 1 5 31 5 1 .f R R.   s   2R 即球面一次折射后成平行光! 被平面镜反射后仍为平行光再次由球面折射: 2 1 1f f s   2Rs  　　　　　 如图所示,一玻璃半球的曲率半径为R，折射率n=1.5， 其平面的一边镀银．一物高为h，放在曲面顶点前2R处．求⑴由球面 所成的第一个像的位置；⑵这一光具组的最后一个像在哪里? 　　　　　 水中的发光体位于距盛水器皿壁x处，从外面往器皿壁 上贴一个平凸透镜，透镜在空气中的焦距等于f．透镜和器皿壁是非 常薄的，水的折射率为 ，而玻璃的折射率 ．物体位于透 镜的主光轴上．求出并讨论像的位置y与物体的位置x的关系．作为 特例，求出x＝f时的像的位置和放大倍数．如果透镜是贴在器皿内壁， 那时候情况是否变化？怎样变化？ 4 3n 水 3 2n 玻 n水 n0 P n玻 -RP  -x 2f R 透镜在空气中焦距为f 由薄透镜成像普适公式 0 0n n nn n n y x R       水 水 1 4 1 1 5 3 2 . y x f    1 1 4 3y f x   3x f y f  当 时 > 0 0< 0 4n y n x    水 续解 透镜是贴在器皿内壁的 P n水 n0n玻 P  由薄透镜成像普适公式 0 0n n nn n n y x R      水 水 -x R 3 4 1 2 3 3 2y x f    4 1 1 3 3y f x   4 fx f y 当 时 4 3   　　　　　 如图所示，两个完全相同的球面薄表壳玻璃合在一起， 中空，其中一块涂银成为球面反射镜．屏上小孔Q为点光源，它发出 的光经反射后成像于 点．调整屏与表壳间的距离L，当L=20 cm时， 像点正好落在屏上．然后在表壳玻璃间注满折射率的水．试问，当L 为何值时，像点仍落在屏上？ Q 设球面曲率半径R,当L=20cm时, 球面镜反射成像物距等 于像距,由球面镜反射成像公式 Q Q L R 1 1 2 L L R   20cmR L  在表壳玻璃间注水 使成一水凸透镜! n0 n水 n0 其像方焦距由 0 0 2 1 n n n n f R R     水 水 2 4 41 11 3 3 30cmf R R      R 续解 L R Q Q n0 n水 n0 R Q对水透镜一次成像Q1,由薄透镜成像公式 1 4 41 11 1 3 3 S L R R        1 1 1 1 30S L    Q1对球面镜二次成像Q2 1 2 1 1 1 10S S     Q2对水透镜三次成像在屏 1 2 1 1 2 S S R     2 1 1 L S   2 1 1 1 30L S    12cmL  4 41 13 3 R R      查阅 　　　　　 如图所示，薄壁球形玻璃鱼缸的半径为R，所盛水的 折射率n＝4/3．鱼缸左侧与轴线垂直的平面反射镜离球心的距离为 3R．一条位于左球面顶点 处的小鱼沿缸壁以速度v游动．从鱼缸右 侧观察鱼的直接像与反射像（先经平面镜反射，再经鱼缸所成的 像）．试求两像之间的相对速度． Q R 3R P O 俯视直接成像光路 2 2s R P 2s 3s -2R r i 由球面折射高斯公式411 3 2 n S R R      水 3RS   -3R 对近轴光线，由几何关系得  3 2 2R r i R r   4 3 in r  水 2r -i 俯视反射像光路 P1 P2 -4R 由球面折射高斯公式 2 4 11 3 4 n S R R     水 2 16S R   P3 P O 续解 O 16R 7 3 R P 4R P3P1 P P2 1 4 3 3 2 v R v R   1 2v v 2 3 16 4 4 v R v R   2 3v v 3 2 4 7 3 3 14 v R v R    v 2v 3v v 3 2 3v v 2 3 v 31 2 23 8 3 vv v v   3 411 3 14 n S R R     水 3 7 3 RS  查阅