九年级数学上册第二十二章二次函数22-1二次函数的图象和性质3y=a(x-h)2教学课件新版 人教版 27页

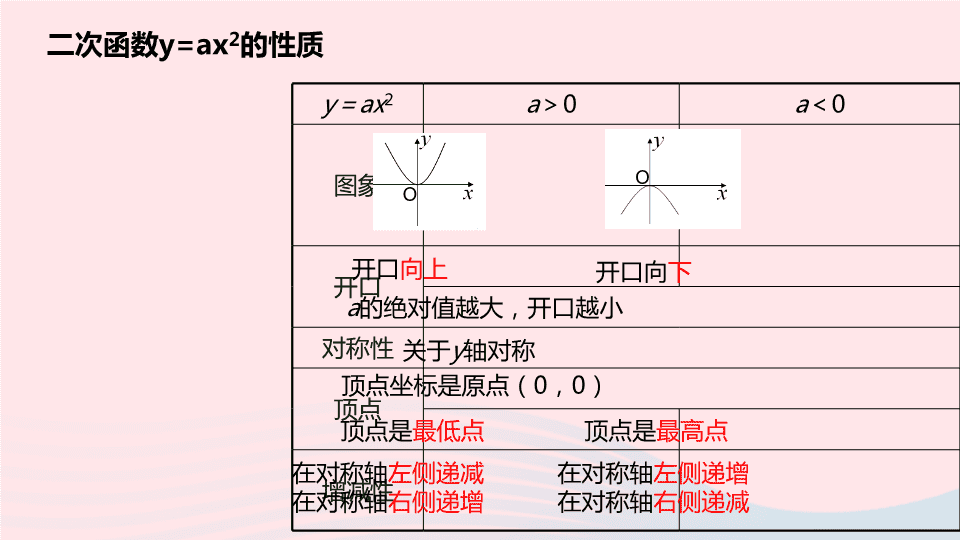
第 22 章：二次函数 22.1 二次函数的图像和性质 22.1.3 y=a(x-h) 2 学习目标： 1.会用描点法画二次函数的图象，并通过图象归纳其性质。 2.理解抛物线与之间的位置关系。 3.灵活运用二次函数的图象及其性质解决问题。 y ＝ ax 2 a ＞ 0 a ＜ 0 图象 开口 对称性 顶点 增减性 开口 向上 开口向 下 a 的绝对值越大，开口越小 关于 y 轴对称 顶点坐标是原点（ 0 ， 0 ） 顶点是 最低点 顶点是 最高点 在对称轴 左侧递减 在对称轴 右侧递增 在对称轴 左侧递增 在对称轴 右侧递减 O O 二次函数y=ax 2 的性质 y ＝ ax 2 +c a>0 a<0 图象 开口 对称性 顶点 增减性 开口 向上 开口向 下 a 的绝对值越大，开口越小 关于 y 轴对称 顶点是 最低点 顶点是 最高点 在对称轴 左侧递减 在对称轴 右侧递增 在对称轴 左侧递增 在对称轴 右侧递减 c>0 c<0 c<0 c>0 (0,c) 二次函数y=ax 2 +c的性质 1 2 3 4 5 x 1 2 3 4 5 6 7 8 9 10 y o -1 -2 -3 -4 -5 抛物线 y=ax 2 +k 可以由抛物线 y=ax 2 向上或向下平移 |k| 得到 . (k>0, 向上平移 ;k<0 向下平移 .) 探究： 1. 在同一坐标系中画出 二次函数 、 以及 的图像 , 并考虑它们的开口方向、对称轴和顶点 . x … -3 -2 -1 0 1 2 3 … 解 : 先列表 描点 -2 … 0 - 0.5 -2 - 0.5 -8 … - 4.5 -8 … -2 -0.5 0 - 4.5 -2 … -0.5 1 2 3 4 5 x -1 -2 -3 -4 -5 -6 -7 -8 -9 1 y o -1 -2 -3 -4 -5 -10 x= － 1 抛物线 与抛物线 、 有什么关系 ? 把抛物线 向右平移 1 个单位 , 就得到抛物线 . 1 2 3 4 5 x -1 -2 -3 -4 -5 -6 -7 -8 -9 1 y o -1 -2 -3 -4 -5 -10 可以发现 , 抛物线 向左平移 1 个单位 , 就得到抛物线 ; 向 左 平移 1 个单位 向 右 平移 1 个单位 即 : 在同一坐标系中作出下列二次函数 : 观察三条抛物线的相互关系 , 并分别指出它们的开口方向 , 对称轴及顶点 . 顶点 (0,0) 顶点 (2,0) 直线 x= － 2 直线 x=2 向 右 平移 2 个单位 向 左 平移 2 个单位 顶点 ( － 2,0) 对称轴 :y 轴 即直线 : x=0 向 右 平移 2 个单位 向 右 平移 2 个单位 向 左 平移 2 个单位 向 左 平移 2 个单位 4. 归纳抛物线 y=a( x -h ) 2 的性质 5. 归纳抛物线 y=a( x -h ) 2 的平移规律 y=a( x -h ) 2 平移规律 :y=a x 2 h < 0 -h > 0 , 左加 , 右减 对于二次函数 请回答下列问题 : 把函数 的图象作怎样的平移变换得 到函数 的图象 . 2. 说出函数 的图象的顶点坐标和对称轴 . 并说明 x 取何值时，函数取最大值？ 顶点是 (6,0), 向右平移 6 个单位 抛物线 对称轴是直线 x=6. 当 x=6 时 , 函数 y 有最大值 ,y 最大 =0 . 如果反过来 , 如何表述 ? 例 1. 画出抛物线 y=2 x 2 ,y=2( x +1 ) 2 , y=2( x -1 ) 2 的草图 . (1) 这三个函数图象的对称轴分别是 、 、 ，顶点分别是 、 、 ． (2) 函数 y=2( x +1 ) 2 的图象可以 看做 y=2( x -1 ) 2 的图象经过怎样 的变化得到的？ y 轴 直线 x=-1 直线 x=1 (0,0) (-1,0) (1,0) +2 左移 y=2( x-1) 2 y=2( x+1) 2 y=2( x+1) 2 y=2( x-1) 2 -2 右移 例 2. 已知 : 抛物线 y=a( x -2 ) 2 经过点 (1,4). 求 :(1) 抛物线的解析式； (2) 抛物线的对称轴、顶点坐标； (3) 当 x=3 时的函数值； (4) 当 x 取何值时， y 随 x 的增大而增大？ 解 : (1)∵ 抛物线 y=a( x -2 ) 2 经过点 (1,4) ∴a=4 ∴ 抛物线的解析式是 y=4( x -2 ) 2 (2) 对称轴是 直线 x=2 ，顶点坐标 (2,0) (3) 当 x=3 时 ,y=4 (4) 当 x>2 时 ,y 随 x 的增大而增大 课堂练习 1. 抛物线 y = –( x +1) 2 的开口向 ，对称轴是 , 顶点坐标是 ； 2. 抛物线 向右平移 2 个单位 , 得到的抛物线是 ； 下 直线 x = –1 (–1 ， 0) 3. 函数 y = –5( x –3) 2 , 当 x______ 时 , y 随 x 的增大而增大； 当 x 时 , y 随 x 的增大而减小。 ＜ 3 ＞ 3 4. 函数 y =4( x +1) 2 的图象是由抛物线 ______ 向 ___ 平移 _____ 个单位得到 . y =4 x 2 左 1 5. 抛物线 y=-2x 2 向下平移 2 个单位得到抛物线 ________, 再向上平移 3 个单得到抛物线 ____________; 若向左平移 2 个单位得到抛物线 _____________ ， 向右平移 2 个单位得到抛物线 _______________. y=-2x 2 +1 y=-2x 2 -2 y=-2 （ x+2 ） 2 y=-2 （ x-2 ） 2 6 、若将抛物线 y=-2 （ x-2 ） 2 的图象的顶点移到原点，则下列平移方法正确的是（ ） A 、向上平移 2 个单位 B 、向下平移 2 个单位 C 、向左平移 2 个单位 D 、向右平移 2 个单位 C 1 、要从抛物线 y= - 2x 2 的图象得到 y= - 2x 2 -1 的图象， 则抛物线 y=-2x 2 必须（ ） . A ．向上平移 1 个单位；       B ．向下平移 1 个单位； C ．向左平移 1 个单位；       D ．向右平移 1 个单位． B 2. 抛物线 y= 2x 2 向上平移 5 个单位 , 会得到哪条抛物线 . 向下平移 3.4 个单位呢 ? 3 、把抛物线 y= 2x 2 -4x+2 化成 y= a(x-h) 2 的形式 , 并指出抛物线的开口方向 , 对称轴 , 顶点坐标 ; 函数有最大值还是最小值 ? 是多少 ? 1. 函数 y=-4x 2 +4x-1 的图象可以由抛物线 y=-4x 2 平移得到吗 ? 应怎样平移 ? 2. 若抛物线 y=2(x-m) m 2 -4m-3 的顶点在 x 轴正半轴上 , 则 m 的值为 ( ) A.m=5 B.m=-1 C.m=5 或 m=-1 D.m=- 5 1. 变式训练 (1) 将抛物线 y=2x 2 向右平移 3 个单位长度，得到抛物线 _____________ . (2) 抛物线 y=2(x+5) 2 是由 y=2x 2 向 平移 个单 位长度得到的 . (3) 抛物线 __________________ 向右平移 4 个单位长度得到 抛物线 y=2(x-1) 2 . y=2(x-3) 2 y=2(x+3) 2 5 左 2. 抛物线 y=3(x+2) 2 的顶点坐标是 ， 对称轴是 ____________ ，图象开口向 ； 当 x ______ 时，函数 y 有最 值，最值为 ； 当 x ______ 时， y 随 x 的增大而减小 . (-2,0) 直线 x=-2 上 =-2 小 0 <-2 3.(1) 下列抛物线的顶点坐标为 (-1,0) 的是 ( ) A.y=x 2 +1 B.y=x 2 -1 C.y=(x+1) 2 D.y=(x-1) 2 (2). 对称轴是直线 x=2 的抛物线是 ( ) A.y=-x 2 +2 B.y=x 2 +2 C.y=3(x+2) 2 D.y=3(x-2) 2 C D 4. 变式训练 (1) 已知二次函数 y=3(x+1) 2 的图象上有三点 A(1,y 1 ),B(2,y 2 ),C(-2,y 3 ), 则 y 1 ,y 2 ,y 3 的大小关系是 ( ) A.y 1 >y 2 >y 3 B.y 2 >y 1 >y 3 C.y 3 >y 1 >y 2 D.y 3 >y 2 >y 1 (2). 已知 A(-1,y 1 ),B(-2,y 2 ),C(3,y 3 ) 三点都在二次函数 y=-2(x+2) 2 的图象上，则 y 1 ,y 2 ,y 3 的大小关系是 . B y 2 >y 1 >y 3 。 5. 抛物线 y=a( x +1 ) 2 经过点 (1,-12). 求 :(1)a 的值； (2) 当 x 在什么范围内取值时， y 随 x 的增大而增大？ 解 : (1)∵ 抛物线 y=a( x +1 ) 2 经过点 (1,-12) ∴4a=-12 ∴a=-3 ∴ 抛物线的解析式是 y =-3( x +1 ) 2 (2) 当 x<-1 时 ,y 随 x 的增大而增大