2020-2021九年级数学上册二次函数单元同步练习1（新人教版pdf格式） 23页

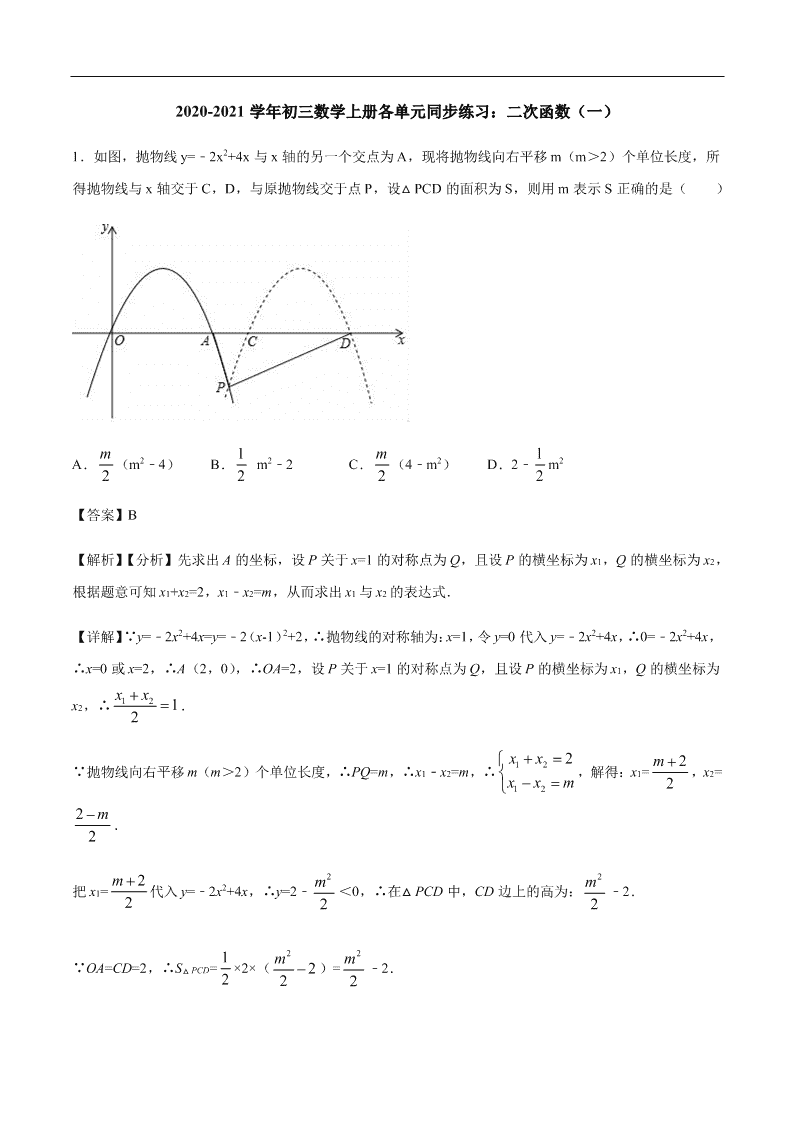
2020-2021 学年初三数学上册各单元同步练习：二次函数（一） 1．如图，抛物线 y=﹣2x2+4x 与 x 轴的另一个交点为 A，现将抛物线向右平移 m（m＞2）个单位长度，所 得抛物线与 x 轴交于 C，D，与原抛物线交于点 P，设△ PCD 的面积为 S，则用 m 表示 S 正确的是（ ） A． 2 m （m2﹣4） B． 1 2 m2﹣2 C． （4﹣m2） D．2﹣ m2 【答案】B 【解析】【分析】先求出 A 的坐标，设 P 关于 x=1 的对称点为 Q，且设 P 的横坐标为 x1，Q 的横坐标为 x2， 根据题意可知 x1+x2=2，x1﹣x2=m，从而求出 x1 与 x2 的表达式． 【详解】∵y=﹣2x2+4x=y=﹣2（x-1）2+2，∴抛物线的对称轴为：x=1，令 y=0 代入 y=﹣2x2+4x，∴0=﹣2x2+4x， ∴x=0 或 x=2，∴A（2，0）， ∴OA=2，设 P 关于 x=1 的对称点为 Q，且设 P 的横坐标为 x1，Q 的横坐标为 x2，∴ 1212 xx  ． ∵抛物线向右平移 m（m＞2）个单位长度，∴PQ=m，∴x1﹣x2=m，∴ 12 12 2xx x x m    ，解得：x1= 2 2 m  ，x2= 2 2 m ． 把 x1= 代入 y=﹣2x2+4x，∴y=2﹣ 2 2 m ＜0，∴在△ PCD 中，CD 边上的高为： ﹣2． ∵OA=CD=2，∴S△ PCD= 1 2 ×2×（ 2 22 m  ）= ﹣2． 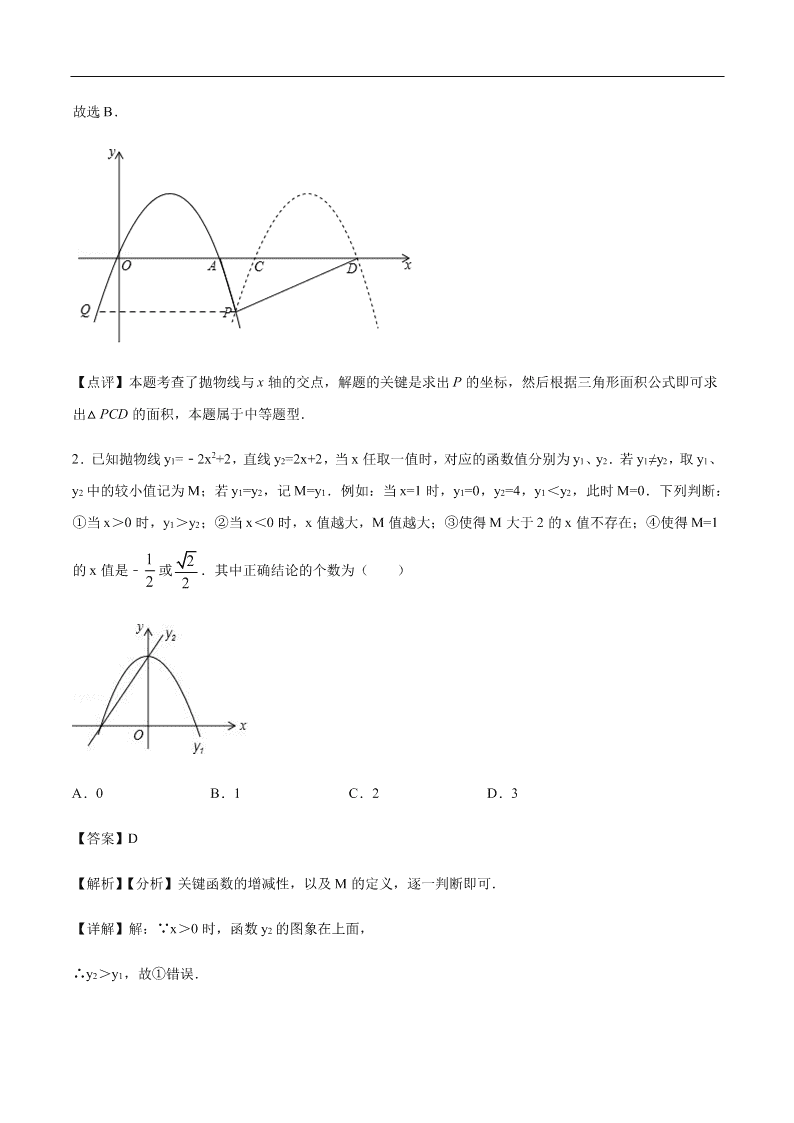故选 B． 【点评】本题考查了抛物线与 x 轴的交点，解题的关键是求出 P 的坐标，然后根据三角形面积公式即可求 出△ PCD 的面积，本题属于中等题型． 2．已知抛物线 y1=﹣2x2+2，直线 y2=2x+2，当 x 任取一值时，对应的函数值分别为 y1、y2．若 y1≠y2，取 y1、 y2 中的较小值记为 M；若 y1=y2，记 M=y1．例如：当 x=1 时，y1=0，y2=4，y1＜y2，此时 M=0．下列判断： ①当 x＞0 时，y1＞y2；②当 x＜0 时，x 值越大，M 值越大；③使得 M 大于 2 的 x 值不存在；④使得 M=1 的 x 值是﹣ 1 2 或 2 2 ．其中正确结论的个数为（ ） A．0 B．1 C．2 D．3 【答案】D 【解析】【分析】关键函数的增减性，以及 M 的定义，逐一判断即可． 【详解】解：∵x＞0 时，函数 y2 的图象在上面， ∴y2＞y1，故①错误． 当 x＜0 时，M 的值=y1 或 y2， ∵x＜0，y 随 x 增大而增大， ∴x 值越大，M 值越大，故②正确． 刚才图象可知 M 的最大值为 2， ∴使得 M 大于 2 的 x 值不存在，故③正确， y2=1 时，x=- 1 2 ， y1=1 时，x=± 2 2 ， 观察图象可知：x=- 或 时，M=1，故④正确． 故选 D． 【点评】本题考查二次函数的性质，解题的关键是理解题意，灵活运用函数的性质解决问题 3．将一元二次方程 23 1 6xx 化为一般式后，二次项系数和一次项系数分别为（ ） A．3，-6 B．3，6 C．3，1 D． 23 , 6xx 【答案】A 【解析】【分析】一元二次方程的一般形式是：ax2+bx+c=0（a，b，c 是常数且 a≠0）特别要注意 a≠0 的条件．这 是在做题过程中容易忽视的知识点．在一般形式中 ax2 叫二次项，bx 叫一次项，c 是常数项．其中 a，b，c 分别叫二次项系数，一次项系数，常数项． 【详解】解 化成一元二次方程一般形式是 23-610xx ，则它的二次项系数是 3，一次项系数 是-6． 故选 A． 【点评】此题主要考查了一元二次方程的一般形式，关键把握要确定一次项系数，首先要把方程化成一般 形式． 4．如图，抛物线 2y x b x c   与 x 轴交于点 A 、 B ，与 y 轴交于点C ， 45OBC  ，则下列各式成立 的是（ ）. A． 10bc   B． 10bc   C． 10bc   D． 10bc   【答案】B 【解析】【分析】根据 ，有 OBOC ，可设点 C、B 的坐标为    0,,0cc、 ，代入解析式， 即可解得答案. 【详解】 ,  OB=OC， 可设点 C、B 的坐标为(0,c)、(c,0)， 把 B(c,0)代入 ，得 2 0,cbcc 即 ( 1) 0c c b   0c  故选：B 【点评】本题考查了抛物线与 x 轴有交点，根据题意得到点 C、B 的坐标是解题的关键. 5．将抛物线 y=3x2+2 向左平移 2 个单位长度，再向下平移 3 个单位长度，则得到的抛物线的解析式为（ ） A．y=3（x﹣2）2﹣1 B．y=3（x﹣2）2+5 C．y=3（x+2）2﹣1 D．y=3（x+2）2+5 【答案】C 【解析】【分析】根据“左加右减、上加下减”的原则进行解答即可． 【详解】将抛物线 y=3x2+2 向左平移 2 个单位所得直线解析式为：y=3（x+2）2+2； 再向下平移 3 个单位为：y=3（x+2）2+2﹣3，即 y=3（x+2）2﹣1． 故选 C． 【点评】本题考查了二次函数图象与几何变换，要求熟练掌握平移的规律：左加右减，上加下减． 6．已知抛物线 y＝ax2＋bx＋c（a<0）过 A（－3，0）， B（1，0）， C（－5，y 1）， D（5，y 2）四点，则 y1 与 y2 的大小关系是（ ） A．y1>y2 B．y1＝y2 C．y1y2， 故选 A． 【点评】本题主要考查二次函数的性质，掌握用抛物线的轴对称性比较二次函数值的大小，是解题的关键． 7．已知二次函数 y＝ax2+bx+c 的部分图象如图所示，下列关于此函数图象的描述中，错误的是（ ） A．对称轴是直线 x＝1 B．当 x＜0 时，函数 y 随 x 增大而增大 C．图象的顶点坐标是（1，4） D．图象与 x 轴的另一个交点是（4，0） 【答案】D 【解析】【分析】利用二次函数的图像与性质，判断选项的正误即可. 【详解】由函数图像可知，对称轴是直线 x＝1 故选项 A 正确；当 x＜0 时，函数 y 随 x 增大而增大，故选 项 B 正确； 图象的顶点坐标是（1，4），故选项 C 正确；图象与 x 轴的另一个交点是（3，0），故选项 D 错误. 故选 D 【点评】本题考查了二次函数的图像与性质，熟练掌握性质是解题的关键. 8．抛物线 y＝﹣ 1 3 （x﹣4)2+1 与坐标轴的交点个数是（ ） A．0 个 B．1 个 C．2 个 D．3 个 【答案】D 【解析】【分析】通过解方程﹣ 1 3 （x﹣4）2+1＝0 可判断抛物线与 x 轴有 2 个交点，通过计算自变量为 0 对应的函数值得到抛物线与 y 轴的交点，从而可判断抛物线 y＝﹣ （x﹣4）2+1 与坐标轴的交点个数． 【详解】解：当 y＝0 时，﹣ （x﹣4）2+1＝0，解得 x1＝4+ 3 ，x2＝4﹣ ，则抛物线与 x 轴的交点 坐标为（4+ 3 ，0），（4﹣ ，0）； 当 x＝0 时，y＝﹣ 1 3 （ x﹣4）2+1＝﹣ 13 3 ，则抛物线与 y 轴的交点坐标为（0，﹣ ）． 故选 D． 【点评】本题考查了抛物线与 x 轴的交点：把求二次函数 y＝ax2+bx+c（a，b，c 是常数，a≠0）与 x 轴 的交点坐标问题转化为解关于 x 的一元二次方程． 9．在下列 4 个不同的情境中，两个变量所满足的函数关系属于二次函数关系的有（ ） ①设正方形的边长为 x 面积为 y，则 y 与 x 有函数关系； ②x 个球队参加比赛，每两个队之间比赛一场，则比赛的场次数 y 与 x 之间有函数关系； ③设正方体的棱长为 x，表面积为 y，则 y 与 x 有函数关系； ④若一辆汽车以 120km/h 的速度匀速行驶，那么汽车行驶的里程 y（km）与行驶时间 x（h）有函数关系． A．1 个 B．2 个 C．3 个 D．4 个 【答案】C 【解析】【分析】根据题意列出函数关系式，然后由二次函数的定义进行判断． 【详解】①依题意得：y=x2，属于二次函数关系，故正确； ②依题意得：y=x（x-1）=x2-x，属于二次函数关系，故正确； ③依题意得：y=6x2，属于二次函数关系，故正确； ④依题意得：y=120x，属于一次函数关系，故错误； 综上所述，两个变量所满足的函数关系属于二次函数关系的有 3 个． 故选 C． 【点评】本题考查二次函数的定义：一般地，形如 y=ax2+bx+c（a、b、c 是常数，a≠0）的函数，叫做二次 函数．其中 x、y 是变量，a、b、c 是常量，a 是二次项系数，b 是一次项系数，c 是常数项．y═ax2+bx+c（a、 b、c 是常数，a≠0）也叫做二次函数的一般形式． 10．二次函数 y=x2+bx+1 的对称轴是直线 x=﹣3，则 b 的值是（ ） A．4 B．5 C．6 D．7 【答案】C 【解析】【分析】由对称轴公式可求得二次函数的对称轴，结合条件可得到关于 b 的方程，可求得 b 的值． 【详解】∵y=x2+bx+1， ∴对称轴为 x=- 2 b ， ∵y=x2+bx+1 的对称轴是直线 x=-3， ∴- =-3，解得 b=6， 故选 C． 【点评】本题主要考查二次函数的对称轴，掌握二次函数的对称轴公式是解题的关键，即二次函数 y=ax2+bx+c（a≠0）的对称轴为 x=- 2 b a ． 11．抛物线 y＝3（x﹣2）2+5 的顶点坐标是（ ） A．（﹣2，5） B．（﹣2，﹣5） C．（ 2，5） D．（ 2，﹣5） 【答案】C 【解析】【分析】根据二次函数的性质 y＝a(x﹣h)2+k 的顶点坐标是(h，k)进行求解即可. 【详解】∵抛物线解析式为 y=3(x-2)2+5， ∴二次函数图象的顶点坐标是(2，5)， 故选 C． 【点评】本题考查了二次函数的性质，根据抛物线的顶点式，可确定抛物线的开口方向，顶点坐标(对称轴)， 最大(最小)值，增减性等． 12．抛物线 y＝x2+x﹣1 的对称轴是（ ） A．直线 x＝﹣1 B．直线 x＝1 C．直线 x＝﹣ 1 2 D．直线 x＝ 【答案】C 【解析】【分析】由对称轴公式 x＝﹣ b 2a 可得对称轴． 【详解】∵对称轴 x＝﹣﹣ ＝﹣ 1 21 ＝﹣ 1 2 ， ∴对称轴是直线 x＝﹣ ． 故选 C． 【点评】本题考查了二次函数的性质，熟练运用对称轴公式．也可以运用配方法写成顶点式求对称轴． 13．如图，抛物线 y＝ 1 4 x2＋x＋3 的顶点为 P，与 y 轴交于点 A，若向右平移 4 个单位，向下平移 4 个单位， 则抛物线上 PA 段扫过的区域(阴影部分)的面积为__________． 【答案】12 【解析】【分析】根据题意求得 A，P 的坐标，再根据平移的性质得到四边形 A PP′A′为平行四边形，以及 A′， P 的坐标，然后求得 AD，PP′的长，再求出面积即可. 【详解】如图，连接 AP，AP′，过点 A 作 AD⊥PP′于 D 点， 由题意可得，四边形 APP′A′为平行四边形， 将 x=0 代入函数得 y=3， ∴点 A 的坐标为（0，3）， 又∵抛物线 y＝ 1 4 x2＋x＋3= (x2+4x+4)+2= (x+2)2+2， ∴顶点 P 的坐标为（﹣2，2）， ∵将抛物线向右平移 4 个单位，向下平移 4 个单位， ∴点 A′(4，﹣1)，点 P′（2，﹣2）， ∴PP′=   2244 =4 2 ，A0=3，∠AOP＝45°， ∴△AOD 为等腰直角三角形， ∴AD=OD， 在 Rt△ AOD 中，AD2+OD2=9，即 2AD2=9， ∴AD= 32 2 ， 则抛物线上 PA 段扫过的区域(阴影部分)的面积为 4 × =12. 故答案为 12. 14．二次函数 y＝ax2+bx+c 的图象与 x 轴相交于（﹣1，0）和（5，0）两点，则该抛物线的对称轴是_____． 【答案】直线 x＝2 【解析】【分析】根据二次函数图象的轴对称性，即可得到答案． 【详解】∵二次函数 y＝ax2+bx+c 的图象与 x 轴相交于(﹣1，0)和(5，0)两点， ∴其对称轴为：直线 x＝ 15 22 -+ = ． 故答案为：直线 x＝2． 【点评】本题主要考查二次函数的轴对称性，掌握二次函数 y＝ax2+bx+c 的图象与 x 轴的交点关于抛物线的 对称轴对称，是解题的关键． 15．抛物线 22 ( 5 ) 3yx    的顶点坐标是__________. 【答案】(-5，-3) 【解析】【分析】由于抛物线 y=a（x-h）2+k 的顶点坐标为（h，k），由此即可求解． 【详解】∵抛物线 y=-2（x+5）2-3， ∴顶点坐标为：（-5，-3）． 故答案为（-5，-3）. 【点评】此题主要考查了二次函数的性质，解题的关键是熟练掌握抛物线的顶点式即可解决问题． 16．拋物线的顶点为（2，﹣3），与 y 轴交于点（0，﹣7），则该抛物线的解析式为_____． 【答案】y=﹣（x﹣2）2﹣3 【解析】【分析】因知道了顶点坐标，所以可设顶点式求解，即设 y=a(x-2)2 -3，然后把（0，﹣7）代入即可 求出 a 的值. 【详解】设 y=a(x-2)2 -3，然后把（0，﹣7）代入，得 -7=a(0-2)2 -3， 解之得， a=-1. ∴y=-(x-2)2 -3. 故答案为 y=-(x-2)2 -3. 【点评】本题考查了待定系数法求二次函数解析式，正确利用顶点式设出函数解析式是解答本题的关键. 17．空地上有一段长为 a 米的旧墙 MN，某人利用旧墙和木栏围成一个矩形菜园 ABCD，已知木栏总长为 100 米． （1）已知 a=20，矩形菜园的一边靠墙，另三边一共用了 100 米木栏，且围成的矩形菜园面积为 450 平方米．如 图 1，求所利用旧墙 AD 的长； （2）已知 0＜α＜50，且空地足够大，如图 2．请你合理利用旧墙及所给木栏设计一个方案，使得所围成的 矩形菜园 ABCD 的面积最大，并求面积的最大值． 【答案】（1）利用旧墙 AD 的长为 10 米．（2）见解析. 【解析】【分析】（1）按题意设出 AD，表示 AB 构成方程； （2）根据旧墙长度 a 和 AD 长度表示矩形菜园长和宽，注意分类讨论 s 与菜园边长之间的数量关系． 【详解】（1）设 AD=x 米，则 AB=100 2 x- 米 依题意得， (100) 2 xx ＝450 解得 x1=10，x2=90 ∵a=20，且 x≤a ∴x=90 舍去 ∴利用旧墙 AD 的长为 10 米． （2）设 AD=x 米，矩形 ABCD 的面积为 S 平方米 ①如果按图一方案围成矩形菜园，依题意 得： S= 2(100)1 (50)125022 xx x ＝ ，0＜x＜a ∵0＜a＜50 ∴x＜a＜50 时，S 随 x 的增大而增大 当 x=a 时，S 最大=50a- 1 2 a2 ②如按图 2 方案围成矩形菜园，依题意得 S= 22(100 2 ) [ (25 )] (25 )2 4 4 x a x a ax     ＝ ，a≤x＜50+ 2 a 当 a＜25+ 4 a ＜50 时，即 0＜a＜ 100 3 时， 则 x=25+ 时，S 最大=（25+ ）2= 210000 200 16 aa， 当 25+ ≤a，即 ≤a＜50 时，S 随 x 的增大而减小 ∴x=a 时，S 最大= (1002) 2 aaa  = 2150 2aa ， 综合①②，当 0＜a＜ 100 3 时， 210000200 16 aa-（ 2150 2aa ）= 2( 3 100) 16 a  ＞0 ＞ ，此时，按图 2 方案围成矩形菜园面积最大，最大面积为 平方米 当 ≤a＜50 时，两种方案围成的矩形菜园面积最大值相等． ∴当 0＜a＜ 时，围成长和宽均为（25+ 4 a ）米的矩形菜园面积最大，最大面积为 平 方米； 当 ≤a＜50 时，围成长为 a 米，宽为（50- 2 a ）米的矩形菜园面积最大，最大面积为（ ）平方 米． 【点评】本题以实际应用为背景，考查了一元二次方程与二次函数最值的讨论，解得时注意分类讨论变量 大小关系． 18．已知 2 43(3)5 mmymx  是关于 x 的二次函数. （1）求 m 的值. （2）当 m 为何值时，该函数图象的开口向上？ （3）当 m 为何值时，该函数有最大值？ 【答案】（1） 5m  或 1m  .（2）当 时，该函数图象的开口向上.（3）当 时，该函数有最大 值. 【解析】【分析】根据题意可知，本题考查是二次函数的基础性质，（1）根据 x 的次数为 2 且二次项系数不 为 0，判断 m 的值；（2）通过二次项系数的正负判断开口方向，为正开口向上，为负开口向下； （3）对任意的 x 值，函数有最大值，在函数开口向下时，函数才有最高点，即二次项系数小于 0。 【详解】解：（1）根据题意，得 2 432, 30, mm m     解得 5 1 , 3. mm m      或 ∴ 5m  或 1m  . （2）∵函数图象的开口向上， ∴ 30m，∴ 3m  ∴ . ∴当 时，该函数图象的开口向上. （3）∵函数有最大值，∴ 30m  . ∴ 3m  ，∴ . ∴当 时，该函数有最大值. 【点评】本题关键点：二次函数 2yaxbxc 中， 0a  ； 0a  时开口向下，函数有最高点，即有最 大值， 0a  时开口向上，函数有最低点，即有最小值。 19．如图，抛物线 y=2（x-2）2 与平行于 x 轴的直线交于点 A，B，抛物线顶点为 C，△ ABC 为等边三角形， 求 S△ ABC; 【答案】 33 4 【解析】【分析】过 B 作 BP⊥x 轴交于点 P，连接 AC，BC，由抛物线 y= 222x（ ）得 C（2，0）， 于是得到对称轴为直线 x=2，设 B（m，n），根据△ ABC 是等边三角形，得到 BC=AB=2m-4，∠BCP=∠ABC=60°， 求出 PB= 3 PC= （m-2），由于 PB=n= 222m（ ），于是得到 3 （m-2）= 222m （ ），解方程得到 m 的值，然后根据三角形的面积公式即可得到结果． 【详解】解：过 B 作 BP⊥x 轴交于点 P，连接 AC，BC， 由抛物线 y= 222x（ ）得 C（2，0）， ∴对称轴为直线 x=2， 设 B（m，n）， ∴CP=m-2， ∵AB∥x 轴， ∴AB=2m-4， ∵△ABC 是等边三角形， ∴BC=AB=2m-4，∠BCP=∠ABC=60°， ∴PB= PC= （m-2）， ∵PB=n= ， ∴ （m-2）= ， 解得 m= 43 2  ，m=2（不合题意，舍去）， ∴AB= ，BP= 3 2 ， ∴S△ ABC= 13333224 ． 【点评】本题考查二次函数的性质. 20．晨光中学课外活动小组准备围建一个矩形生物苗圃园，其中一边靠墙，另外三边用长为 30 米的篱笆围 成．已知墙长为 18 米（如图所示），设这个苗圃园垂直于墙的一边的长为 x 米． (1)若平行于墙的一边长为 y 米，直接写出 y 与 x 的函数关系式及其自变量 x 的取值范围； (2)设这个苗圃园的面积为 S，求 S 与 x 之间的函数关系． 【答案】（1）y＝30﹣2x，（ 6≤x＜15）；（2）S＝﹣2（x﹣7.5）2+112.5． 【解析】【分析】（1）由总长度−垂直于墙的两边的长度=平行于墙的这边的长度，根据墙的长度就可以求出 x 的取值范围； （2）由长方形的面积公式建立二次函数即可. 【详解】解：（1）y＝30﹣2x，（ 6≤x＜15）； （2）设矩形苗圃的面积为 S S＝xy＝x（30﹣2x）＝﹣2（x﹣7.5）2+112.5． 【点评】此题考查了二次函数的实际应用问题.解题的关键是根据题意构建二次函数模型. 21．已知二次函数 y=x2+3x+m 的图象与 x 轴交于点 A（﹣4，0）． （1）求 m 的值； （2）求该函数图象与坐标轴其余交点的坐标． 【答案】（1）m=-4；（ 2）（ 0，﹣4），（ 1，0）． 【解析】【分析】（1）将 A 点坐标（﹣4，0）代入 y=x2+3x+m，即可求解； （2）令 x=0 时，则：y=﹣4，令 y=0，则 x2+3x﹣4=0，即可求解． 【详解】（1）将 A 点坐标（﹣4，0）代入 y=x2+3x+m 得：16﹣12+m=0，解得：m=﹣4； （2）当 x=0 时，则：y=﹣4，∴函数图象与 y 轴的交点为（0，﹣4）． 令 y=0，则 x2+3x﹣4=0，解得：x1=1，x2=﹣4，∴函数图象与 x 轴的另一个交点为（1，0）． 【点评】本题考查了抛物线与坐标轴的交点，是二次函数基础类题目． 22．图中是抛物线形拱桥，当拱顶离水面 2m 时，水面宽 4m，建立如图所示的平面直角坐标系： （1）求拱桥所在抛物线的解析式； （2）当水面下降 1m 时，则水面的宽度为多少？ 【答案】（1）y=﹣ 1 2 x2+2;（2） 26 【解析】【分析】（1）设出抛物线解析式，由已知条件求出点 B、点 C 的坐标，将 B、C 的坐标代入抛物线 解析式，列方程组求出未知参数即可；（2）令 y=﹣1，解出 x，即可求出水面的宽度. 【详解】解：（1）由题意设抛物线解析式为：y=ax2+b（a≠0）， ∵当拱顶离水面 2m 时，水面宽 4m， ∴点 C（0，2），点 B（2，0）， 代入得： 2 40 b ab    ， 解得： 1 2 2 a b     ， ∴拱桥所在抛物线的解析式为 y=﹣ 1 2 x2+2； （2）当水位下降 1m 时，水位纵坐标为﹣1， 令 y=﹣1， 则﹣1=﹣ x2+2， 解得 x=± 6 ， ∴水面宽度为 2 米. 【点评】本题主要考查二次函数的应用，建立直角坐标系，求出抛物线的解析式是解题的关键. 23．如图，在△ ABC 中，∠B=90°，AB=12，BC=24，动点 P 从点 A 开始沿边 AB 向终点 B 以每秒 2 个单 位长度的速度移动，动点 Q 从点 B 开始沿边 BC 以每秒 4 个单位长度的速度向终点 C 移动，如果点 P、Q 分别从点 A、B 同时出发，那么△ PBQ 的面积 S 随出发时间 t（s）如何变化？写出函数关系式及 t 的取值范 围． 【答案】y=﹣4t2+24t（0＜t＜6） 【解析】【分析】先根据两点移动速度以及移动方向得出 BP 以及 BQ 的长；然后根据所求三角形的面积与 时间的关系，得出 S 与 t 的函数关系式；最后根据动点在直角三角形的直角边上运动的时间，求出 t 的取值 范围即可. 【详解】△ PBQ 的面积 S 随出发时间 t（s）成二次函数关系变化， ∵在△ ABC 中，∠B=90°，AB=12，BC=24，动点 P 从点 A 开始沿边 AB 向终点 B 以每秒 2 个单位长度的 速度移动，动点 Q 从点 B 开始沿边 BC 以每秒 4 个单位长度的速度向终点 C 移动， ∴BP=12﹣2t，BQ=4t， ∴△PBQ 的面积 S 随出发时间 t（s）的解析式为：y= (12﹣2t）×4t=﹣4t2+24t，（ 0＜t＜6）． 【点评】本题考查了二次函数的应用---动点的函数问题，用含 t 的代数式表示出 BP 以及 BQ 的长是解答本 题的关键. 24．在平面直角坐标系中，平行四边形퐴퐵푂퐶如图放置，点퐴、퐶的坐标分别是(0,  4)、(−1,  0)，将此平行四 边形绕点푂顺时针旋转90∘，得到平行四边形퐴′퐵′푂퐶′． (1)如抛物线经过点퐶、퐴、퐴′，求此抛物线的解析式； (2)在(1)情况下，点푀是第一象限内抛物线上的一动点，问：当点푀在何处时，△ 퐴푀퐴′的面积最大？最大 面积是多少？并求出此时푀的坐标； (3)在(1)的情况下，若푃为抛物线上一动点，푁为푥轴上的一动点，点푄坐标为(1, 0)，当푃、푁、퐵、푄构成以 퐵푄作为一边的平行四边形时，求点푃的坐标． 【答案】(1) 抛物线的解析式为：푦 = −푥2 + 3푥 + 4；(2) 当푥 = 2时，△ 퐴푀퐴′的面积最大，最大值푆△퐴푀퐴′ = 8， 푀的坐标为：(2, 6)；(3) 点푃的坐标为：푃1(0, 4)，푃2(3, 4)，푃3(3+√41 2 , −4)，푃4(3−√41 2 , −4) 【解析】【分析】（1）由平行四边形 ABOC 绕点 O 顺时针旋转 90°，得到平行四边形 A′B′OC′，且点 A 的坐 标是（0，4），可求得点 A′的坐标，然后利用待定系数法即可求得经过点 C、A、A′的抛物线的解析式； （2）首先连接 AA′，设直线 AA′的解析式为：y=kx+b，利用待定系数法即可求得直线 AA′的解析式，再设 点 M 的坐标为：（x，-x2+3x+4），继而可得△ AMA′的面积，继而求得答案； （3）分别从 BQ 为边与 BQ 为对角线去分析求解即可求得答案． 【详解】解：(1)∵平行四边形퐴퐵푂퐶绕点푂顺时针旋转90∘，得 到平行四边形퐴′퐵′푂퐶′，且点퐴的坐标是(0, 4)， ∴点퐴′的坐标为：(4,  0)， ∵点퐴、퐶的坐标分别是(0, 4)、(−1,  0)，抛物线经过点퐶、퐴、퐴′， 设抛物线的解析式为：푦 = 푎푥2 + 푏푥 + 푐， ∴{ 푎 − 푏 + 푐 = 0 푐 = 4 16푎 + 4푏 + 푐 = 0 ， 解得：{ 푎 = −1 푏 = 3 푐 = 4 ， ∴此抛物线的解析式为：푦 = −푥2 + 3푥 + 4； (2)连接퐴퐴′，设直线퐴퐴′的解析式为：푦 = 푘푥 + 푏， ∴{ 푏 = 4 4푘 + 푏 = 0 ， 解得：{푘 = −1 푏 = 4 ， ∴直线퐴퐴′的解析式为：푦 = −푥 + 4， 设点푀的坐标为：(푥, −푥2 + 3푥 + 4)， 则푆△퐴푀퐴′ = 1 2 × 4 × [−푥2 + 3푥 + 4 − (−푥 + 4)] = −2푥2 + 8푥 = −2(푥 − 2)2 + 8， ∴当푥 = 2时，△ 퐴푀퐴′的面积最大，最大值푆△퐴푀퐴′ = 8， ∴푀的坐标为：(2,  6)； (3)设点푃的坐标为(푥, −푥2 + 3푥 + 4)，当푃，푁，퐵，푄构成平行四边形时， ∵平行四边形퐴퐵푂퐶中，点퐴、퐶的坐标分别是(0,  4)、(−1, 0)， ∴点퐵的坐标为(1, 4)， ∵点푄坐标为(1,  0)，푃为抛物线上一动点，푁为푥轴上的一动点， ①当퐵푄为边时，푃푁 // 퐵푄，푃푁 = 퐵푄， ∵퐵푄 = 4， ∴−푥2 + 3푥 + 4 = ±4， 当−푥2 + 3푥 + 4 = 4时，解得：푥1 = 0，푥2 = 3， ∴푃1(0, 4)，푃2(3, 4)； 当−푥2 + 3푥 + 4 = −4时，解得：푥3 = 3+√41 2 ，푥4 = 3−√41 2 ， ∴푃3(3+√41 2 , −4)，푃4(3−√41 2 , −4)； ②当퐵푄为对角线时，퐵푃 // 푄푁，퐵푃 = 푄푁，此时푃与푃1，푃2重合； 综上可得：点푃的坐标为：푃1(0,  4)，푃2(3,  4)，푃3(3+√41 2 , −4)，푃4(3−√41 2 , −4) 【点评】此题属于二次函数的综合题，考查了待定系数法求函数解析式的知识、平行四边形的性质以及三 角形面积问题．掌握分类讨论思想的应用是解此题的关键．