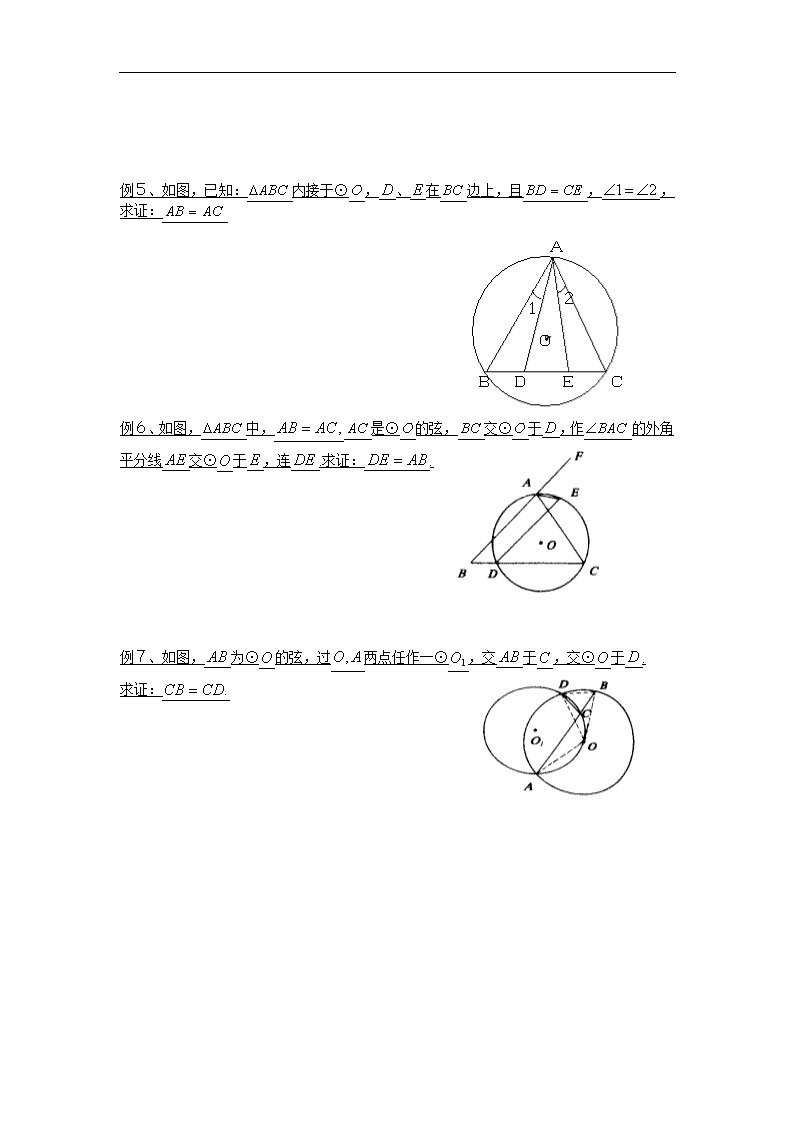中考数学专题复习练习：圆周角定理内容 3页

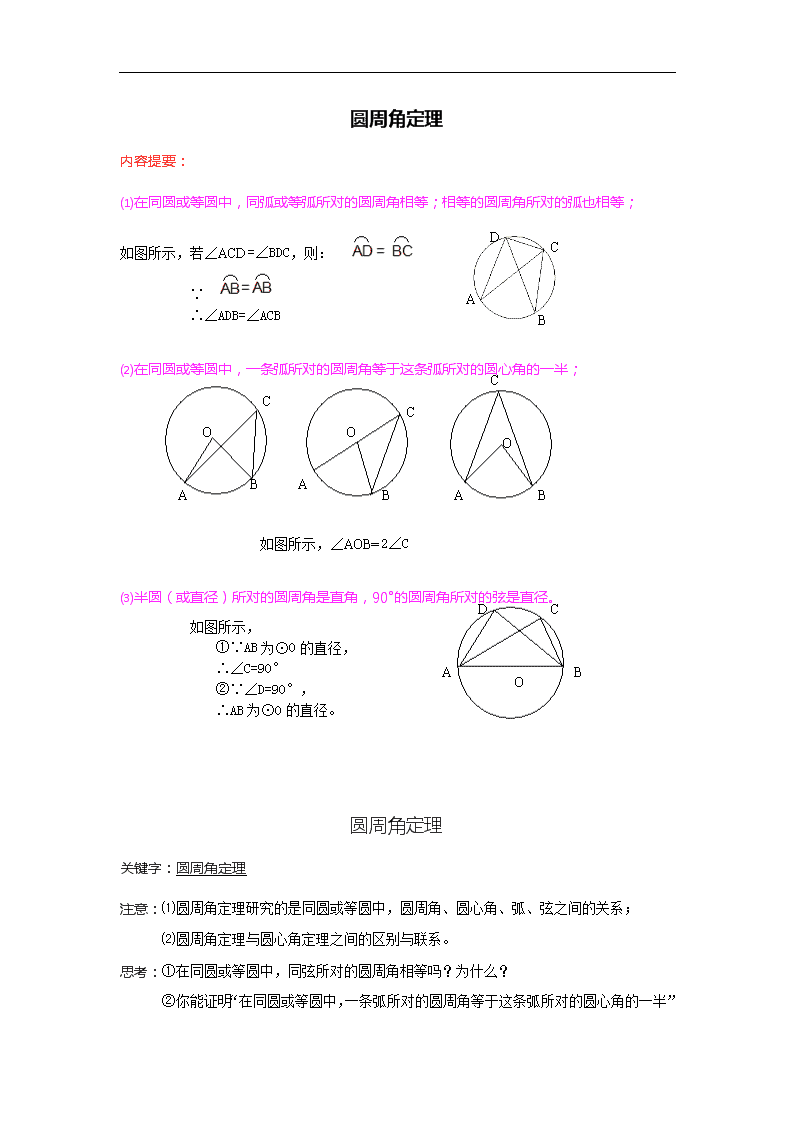
圆周角定理 内容提要：‎ ‎⑴在同圆或等圆中，同弧或等弧所对的圆周角相等；相等的圆周角所对的弧也相等；‎ B A D C 如图所示，若∠ACD=∠BDC，则：‎ ‎ ∵‎ ‎ ∴∠ADB=∠ACB A A A C C C O O O B B B ‎⑵在同圆或等圆中，一条弧所对的圆周角等于这条弧所对的圆心角的一半；‎ ‎ 如图所示，∠AOB=2∠C A B C D O ‎⑶半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径。‎ ‎ 如图所示，‎ ‎①∵AB为⊙O的直径，‎ ‎∴∠C=90°‎ ‎②∵∠D=90°，‎ ‎∴AB为⊙O的直径。‎ 圆周角定理 关键字：圆周角定理 注意：⑴圆周角定理研究的是同圆或等圆中，圆周角、圆心角、弧、弦之间的关系；‎ ‎⑵圆周角定理与圆心角定理之间的区别与联系。‎ 思考：①在同圆或等圆中，同弦所对的圆周角相等吗？为什么？‎ ‎②你能证明“在同圆或等圆中，一条弧所对的圆周角等于这条弧所对的圆心角的一半”‎ 吗？试一试。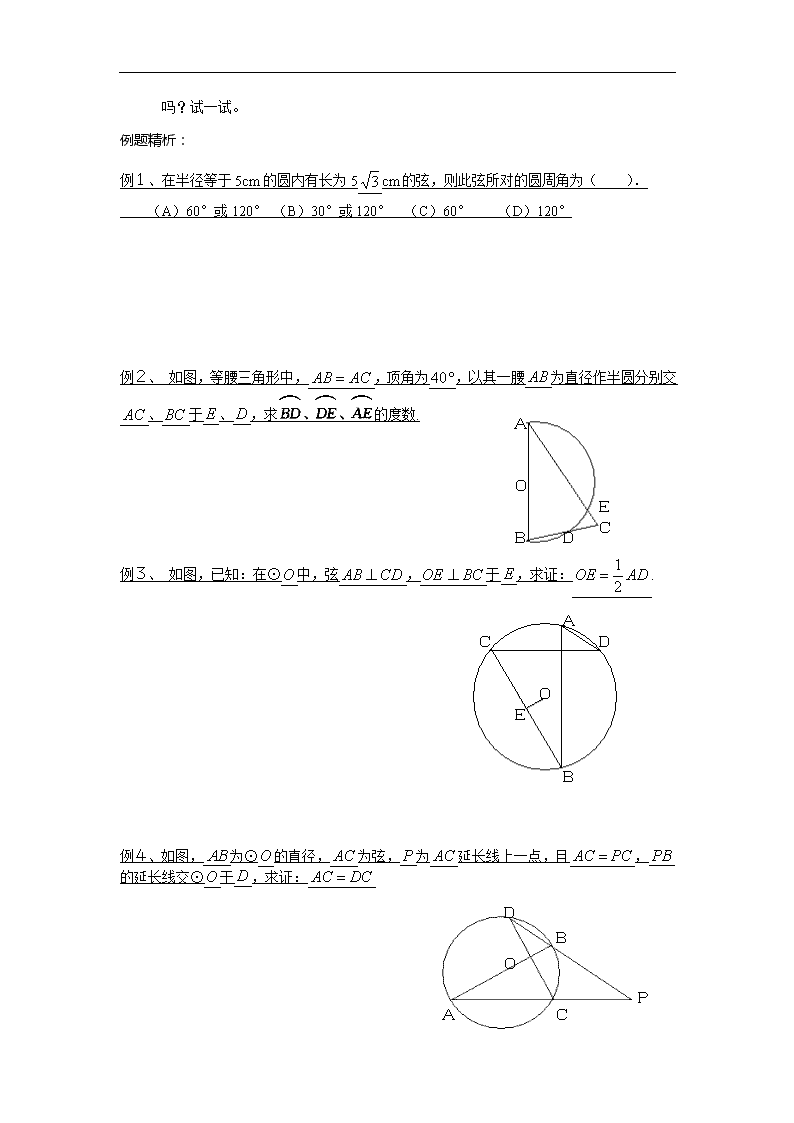‎ 例题精析：‎ 例１、在半径等于5cm的圆内有长为5cm的弦，则此弦所对的圆周角为（ ）．‎ ‎ （A）60°或120° （B）30°或120° （C）60° （D）120°‎ Ａ Ａ Ｂ Ｃ Ｄ Ｅ Ｏ 例２、 如图，等腰三角形中，，顶角为，以其一腰为直径作半圆分别交、于、，求的度数.‎ Ｃ Ｄ Ａ Ｂ Ｅ Ｏ 例３、 如图，已知：在⊙中，弦，于，求证：.‎ Ａ Ａ Ｂ Ｐ Ｃ Ｄ Ｏ 例４、如图，为⊙的直径，为弦，为延长线上一点，且，的延长线交⊙于，求证：‎ Ａ Ｂ Ｃ Ｄ Ｅ Ｏ ‎１‎ ‎２‎ 例５、如图，已知：内接于⊙，、在边上，且，，求证：‎ 例６、如图，中，是⊙的弦，交⊙于，作的外角平分线交⊙于，连.求证：.‎ 例７、如图，为⊙的弦，过两点任作一⊙，交于，交⊙于.‎ 求证：‎