- 620.37 KB
- 2021-12-06 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
1
组合体的体积(2019.4)
教学内容:五年级第二学期 P51 组合体的体积
教学目标:
1、会用切割或填补的方法把组合体切割或填补成我们学过的正方体
和长方体。
2、会合理切割,填补找到有效数据计算简单组合体的体积。
3、能找到书本前后知识间的联系,合理运用已有的知识经验解决新问
题,体验成功的乐趣。
教学重点:将组合体切割成几个长方体与正方体并计算简单组合体的
体积。
教学难点:引导学生合理切割填补,找到有效数据。
教学准备:多媒体课件。
学情分析:学生已经认识了简单的组合体,能分辨出本课中的组合体
都是由简单的长方体和正方体组成。学生能正确求出长方体和正方体
的体积,有了求组合图形的面积的学习经验,会用切割法和填补法求
组合图形的面积。
教学策略:本课拟用知识迁移教学策略,学生已有了求组合图形面积
的经验,加上求长方体和正方体体积的相关知识,将已有的知识经验
迁移到本课教学中,便于学生习得求组合体体积的知识技能。
学习策略:迁移类推学习策略。迁移和类推是学生在数学学习中广泛
采用的学习策略,特别是那些与旧知识联系比较紧密的新知识的学习
更是离不开顺向迁移和类推。顺向迁移是指先前的学习对后继学习的
影响,求组合图形的面积用的切割填补法可以迁移到组合体体积这一
教学内容中。类推可以引导学习者借鉴过去所学习的知识和方法去推
出新知识,它是学生获取新知识的重要途径。
教学过程:
一. 激活旧知:
1、在期中阶段练习中,压轴题是
关于这个组合体的体积,在练习的时候我们并
没有学习过它的解题方法,但是出乎我的意料
我们班有 20 位同学已经能够正确求出它的体
积了。
2
我们先来回顾一下同学们的解题方法,并请这些同学来介绍一下,在
解题过程中你们的思考过程。
2、听了同学们的介绍,在解题过程中运用到了哪些我们过去学过的知
识?
板书 切割、填补
3、原来没有做对的同学你是碰到了什么困难?
二、求证新知
1、听了成功同学的经验,我们一起来试一试今天的例题。
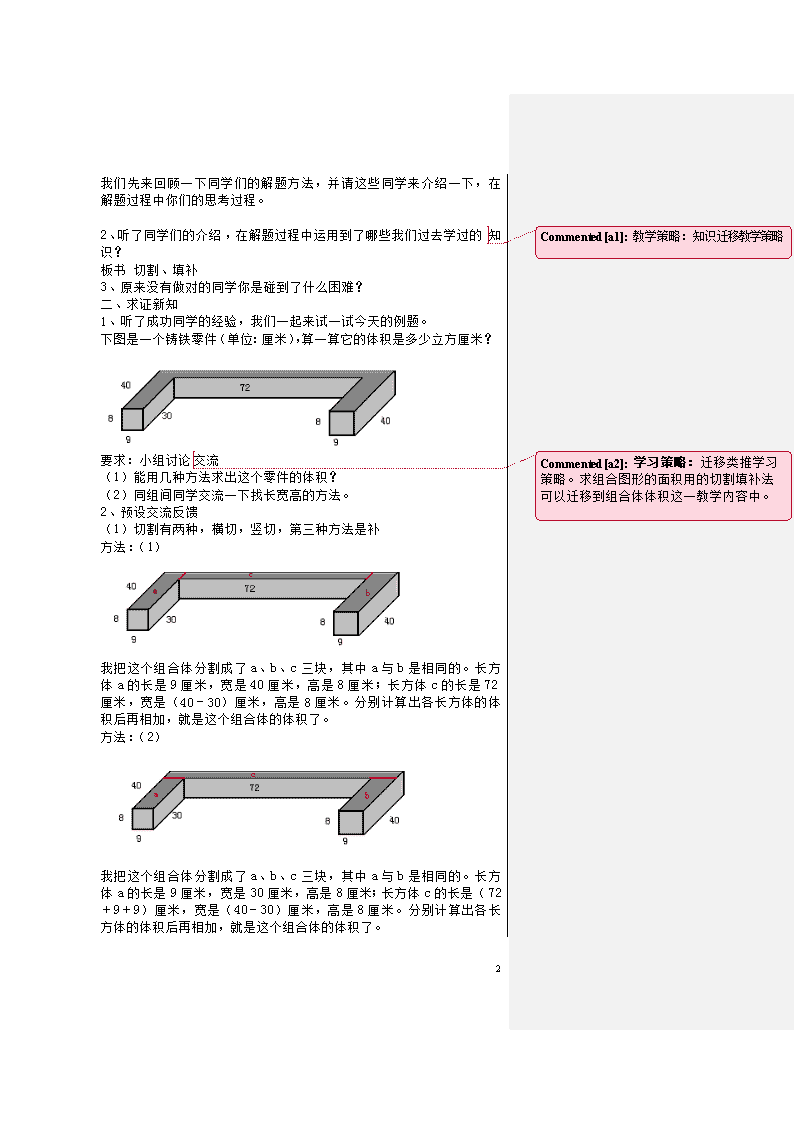
下图是一个铸铁零件(单位:厘米),算一算它的体积是多少立方厘米?
要求:小组讨论交流
(1)能用几种方法求出这个零件的体积?
(2)同组间同学交流一下找长宽高的方法。
2、预设交流反馈
(1)切割有两种,横切,竖切,第三种方法是补
方法:(1)
我把这个组合体分割成了 a、b、c 三块,其中 a 与 b 是相同的。长方
体 a 的长是 9 厘米,宽是 40 厘米,高是 8 厘米;长方体 c 的长是 72
厘米,宽是(40-30)厘米,高是 8 厘米。分别计算出各长方体的体
积后再相加,就是这个组合体的体积了。
方法:(2)
我把这个组合体分割成了 a、b、c 三块,其中 a 与 b 是相同的。长方
体 a 的长是 9 厘米,宽是 30 厘米,高是 8 厘米;长方体 c 的长是(72
+9+9)厘米,宽是(40-30)厘米,高是 8 厘米。分别计算出各长
方体的体积后再相加,就是这个组合体的体积了。
3
小结:切割是可以先把组合体切割成几个可以计算出体积的长方体或
正方体,分别计算体积后再相加。
板书:先切割再相加
方法(3)
在空缺处补成一完整的长方体,求出总体积再减去补上部分的体积。
完整长方体的长是 72+9+9 厘米,宽是 40 厘米,高是 8 厘米;补上部
分长方体的长是 72,宽是 30,高是 8。先求出完整的长方体的体积再
减去补上部分的长方体的体积就是组合体的体积。
小结:填补可以先在空缺处补上长方体或正方体,求出总体积再减去
补上部分的体积。
板书:先填补在相减
三、尝试应用
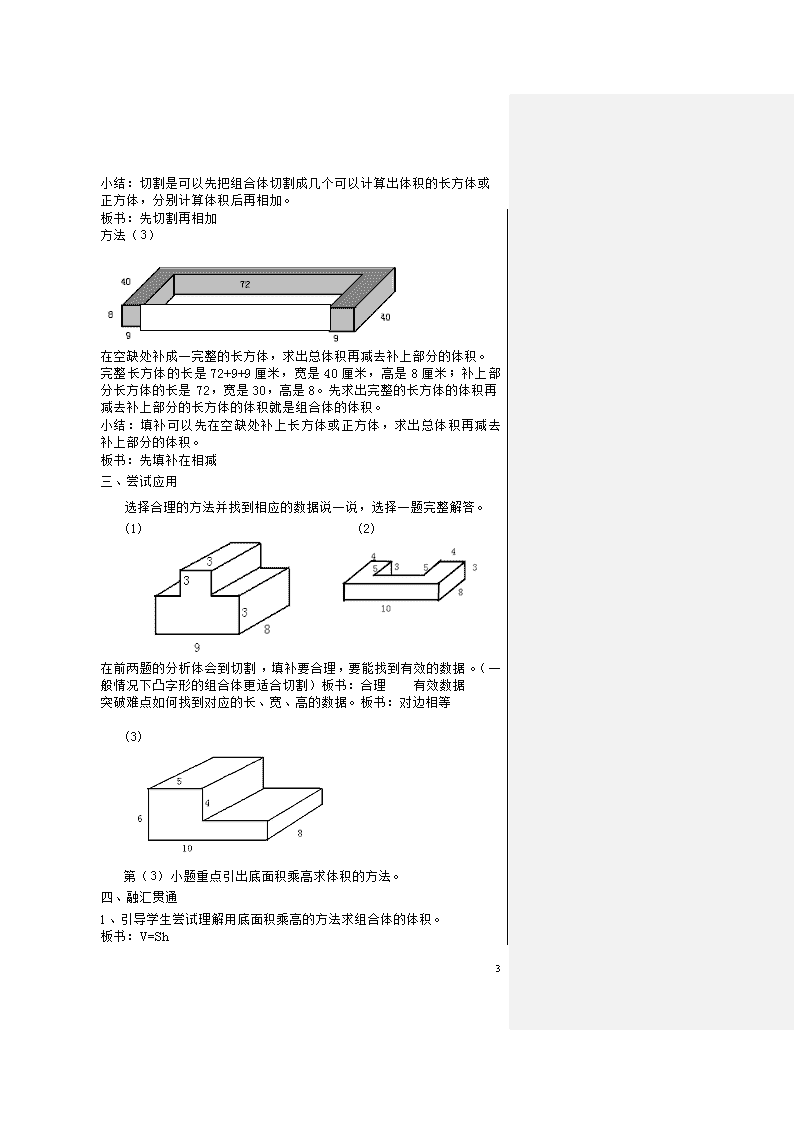
选择合理的方法并找到相应的数据说一说,选择一题完整解答。
(1) (2)
在前两题的分析体会到切割,填补要合理,要能找到有效的数据。(一
般情况下凸字形的组合体更适合切割)板书:合理 有效数据
突破难点如何找到对应的长、宽、高的数据。板书:对边相等
(3)
第(3)小题重点引出底面积乘高求体积的方法。
四、融汇贯通
1、引导学生尝试理解用底面积乘高的方法求组合体的体积。
板书:V=Sh
4
组合体的体积
体积与重量
2、注意这种方法的局限性。
3、例题中的铸铁零件,每立方厘米重 7.85 克,这个零件有多重?
板书:体积与重量
4、总结:知识不是独立的,而是相互关联的,甚至不同学科间的知识
也是相通的,试着理清知识点之间的脉络才能取得事半功倍的效果。
板书设计
组合体的体积
切割法:先切割后相加
组合图形的面积
合理
有效数据(对边相等)
填补法:先填补后相减