小学五年级奥数教案：加法原理和乘法原理综合(学生版) 6页

‎ 学科培优 数学 ‎ ‎“加法原理和乘法原理综合”‎ 学生姓名 授课日期 教师姓名 授课时长 知识定位 本讲力求让学生懂得并运用加法乘法原理来解决问题，掌握常见的计数方法，会使用这些方法来解决问题 知识梳理 乘法原理 我们在完成一件事时往往要分为多个步骤，每个步骤又有多种方法，当计算一共有多少种完成方法时就要用到乘法原理.‎ 乘法原理：一般地，如果完成一件事需要n个步骤，其中，做第一步有m1种不同的方法，做第二步有m2种不同的方法 ，…，做第n步有mn种不同的方法，则完成这件事一共有N=m1×m2×…×mn种不同的方法．‎ 乘法原理运用的范围：这件事要分几个彼此互不影响的独立步骤来完成，这几步是完成这件任务缺一不可的，这样的问题可以使用乘法原理解决．我们可以简记为：“乘法分步，步步相关”.‎ 加法原理 无论自然界还是学习生活中，事物的组成往往是分门别类的，例如解决一件问题的往往不只一类途径，每一类途径往往又包含多种方法，如果要想知道一共有多少种解决方法，就需要用到加法原理.‎ 加法原理：一般地，如果完成一件事有k类方法，第一类方法中有m1种不同做法，第二类方法中有m2种不同做法 ，…，第k类方法中有mk种不同的做法，则完成这件事共有N= m1 + m2 +…+mk 种不同的方法.‎ 加法原理运用的范围：完成一件事的方法分成几类，每一类中的任何一种方法都能完成任务，这样的问题可以使用加法原理解决．我们可以简记为：“加法分类，类类独立”.‎ 例题精讲 ‎【试题来源】‎ ‎【题目】从五年级8个班中评选出学习、体育、卫生先进集体，如果要求同一个班级只能得 到一个先进集体，那么一共有多少种评选方法？‎ ‎【试题来源】‎ ‎【题目】用5种不同颜色的笔来写“智康教育”这几个字，相邻的字颜色不同，共有多少种写法？‎ ‎【试题来源】‎ ‎【题目】北京到广州之间有10个站，其中只有两个站是大站（不包括北京、广州），从大站出发的车辆可以配卧铺，那么铁路局要准备多少种不同的卧铺车票？‎ ‎【试题来源】‎ ‎【题目】7个相同的球放在4个不同的盒子里，每个盒子至少放一个，不同的放法有多少种？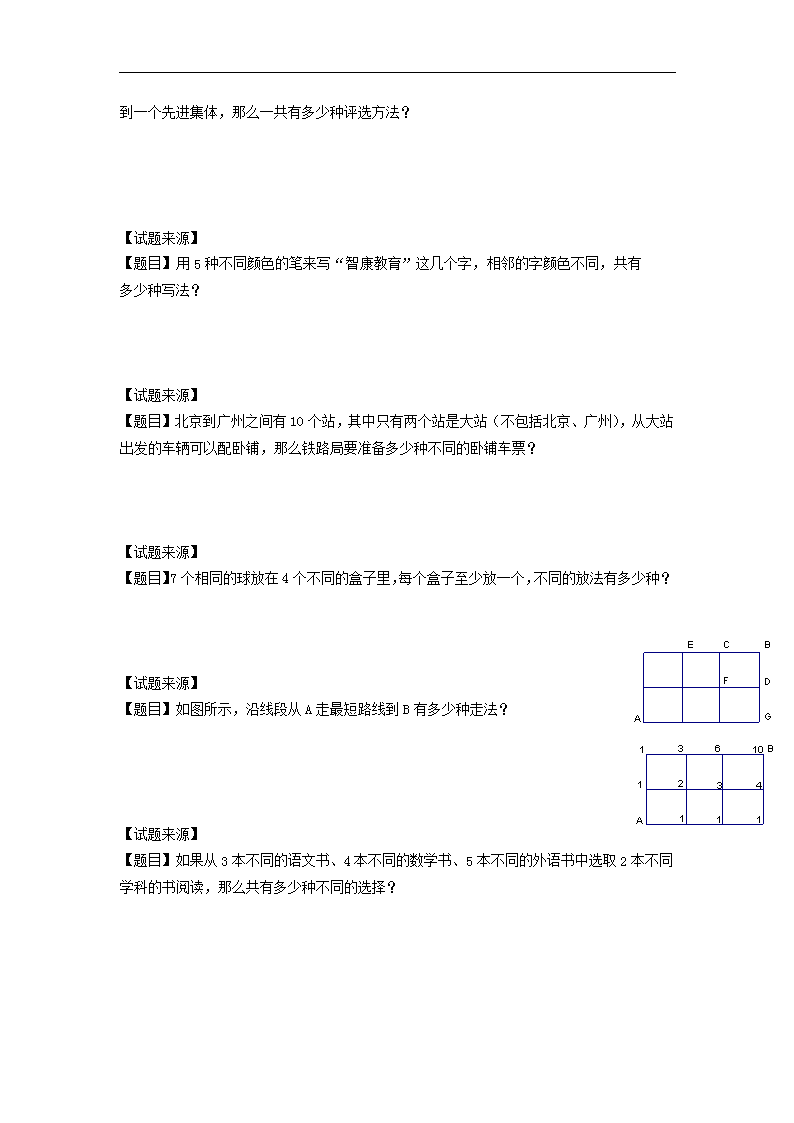‎ ‎【试题来源】‎ ‎【题目】如图所示，沿线段从A走最短路线到B有多少种走法？‎ ‎【试题来源】‎ ‎【题目】如果从3本不同的语文书、4本不同的数学书、5本不同的外语书中选取2本不同学科的书阅读，那么共有多少种不同的选择？‎ ‎【试题来源】‎ ‎【题目】用1，2，3，4这4个数字，组成各位数字互不相同的四位数，例如1234，4321等，求全体这样的四位数之和．‎ ‎【试题来源】‎ ‎【题目】某条铁路线上，包括起点和终点在内原来共有7个车站，现在新增了3个车站，铁路上两站之间往返的车票不一样，那么，这样需要增加多少种不同的车票？‎ ‎【试题来源】‎ ‎【题目】用0～9这十个数字可组成多少个无重复数字的四位数.‎ ‎【试题来源】‎ ‎【题目】12个人围成一圈，从中选出三个人，其中恰有两人相邻，共有多少种不同选法？‎ ‎【试题来源】‎ ‎【题目】A、B、C三个小朋友互相传球，先从A开始发球(作为第一次传球)，这样经过了5次传球后，球恰巧又回到A手中，那么不同的传球方式共多少种． ‎ ‎【试题来源】‎ ‎【题目】在2000到2999这1000个自然数中，有多少个千位、百位、十位、个位数字中恰有两个相同的数？‎ ‎【试题来源】‎ ‎【题目】将一些数字分别填入下列各表中，要求每个小格中填入一个数字，表中的每横行中从左到右数字由小到大，每一竖列中从上到小数字也由小到大排列。‎ ‎(1)将1至4填入表1中，方法有_________种；‎ ‎(2)将1至6填入表2中，方法有_________种；‎ ‎【试题来源】‎ ‎【题目】某人忘记了自己的密码数字，只记得是由四个非0数码组成，且四个数码之和是9.为确保打开保险柜至少要试多少次？．‎ ‎【试题来源】‎ ‎【题目】五位同学扮成奥运会吉祥物福娃贝贝、晶晶、欢欢、迎迎和妮妮，排成一排表演节目。如果贝贝和妮妮不相邻，共有（ ）种不同的排法。‎ ‎【试题来源】‎ ‎【题目】一种电子表在6时24分30秒时的显示为6:24，那么从8时到9时这段时间里，此表的5个数字都不相同的时刻一共有多少个?‎ ‎【试题来源】‎ ‎【题目】在1000至1999这些自然数中个位数大于百位数的有多少个?‎ ‎【试题来源】‎ ‎【题目】同时满足以下条件的分数共有多少个?‎ ‎ ①大于，并且小于；‎ ‎②分子和分母都是质数；‎ ‎③分母是两位数．‎ ‎【试题来源】‎ ‎【题目】一个自然数，如果它顺着看和倒过来看都是一样的，那么称这个数为“回文数”．例如1331，7，202都是回文数，而220则不是回文数．问：从一位到六位的回文数一共有多少个?其中的第1996个数是多少?‎ ‎【试题来源】‎ ‎【题目】有9张同样大小的圆形纸片，其中标有数码“1”的有1张，标有数码“2”的有2张，标有数码“3”的有3张，标有数码“4”的有3张，把这9张圆形纸片如呼所示放置在一起，但标有相同数码的纸片不许*在一起。 ⑴如果M处放标有数码“3”的纸片，一共有多少种不同的放置方法？ ⑵如果M处放标有数码“2”的纸片，一共有多少种不同的放置方法？‎ 习题演练 ‎【试题来源】‎ ‎【题目】在20世纪中，有些年的年份数是由4个不相同的数字组成的，这样的年份共有 个．‎ ‎【试题来源】‎ ‎【题目】一只青蛙在A，B，C三点之间跳动，若青蛙从A点跳起，跳4次仍回到A点，则这只青蛙一共有多少种不同的跳法？‎ ‎【试题来源】‎ ‎【题目】有黑白两种棋子共300枚，按每堆3枚分成100堆.其中只有1枚白子的共27堆；有2枚或3枚黑子的共42堆；有3枚白子的与有3枚黑子的堆数相等.那么在全部棋子中，白子共有___枚.‎ ‎【试题来源】‎ ‎【题目】世界杯小组赛由4个球队进行单循环赛，安排这四个球队先后比赛次序，有几种方法？‎ ‎【试题来源】‎ ‎【题目】三个工厂共订300份报纸，每个工厂至少订了99份，至多101份，问：一共有多少种不同的订法？‎ ‎【试题来源】‎ ‎【题目】小明的两个衣服口袋中各有13张卡片，每张卡片上分别写着1，2，3，…，13．如果从这两个口袋中各拿出一张卡片来计算它们所写两数的乘积，可以得到许多不相等的乘积．那么，其中能被6整除的乘积共有多少个?‎