人教版5年级上数学教学课件：三角形的面积 26页

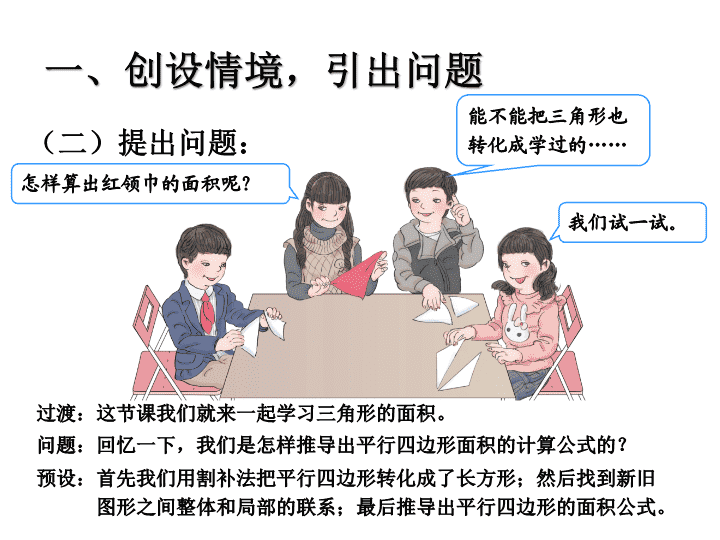
三角形的面积 多边形的面积 一、创设情境，引出问题 （一）出示情境： 一、创设情境，引出问题 （二）提出问题： 过渡： 这节课我们就来一起学习 三角形 的面积。 问题： 回忆一下，我们是 怎样推导出平行四边形 面积的计算公式的？ 预设： 首先 我们用割补法把平行四边形转化成了长方形；然后找到新旧 图形之间 整体 和局部的联系； 最后推导 出平行四边形的面积公式。 怎样算出红领巾的面积呢？ 能不能把三角形也转化成学过的 …… 我们试一试。 二、动手实践，深入探究 （一）借助拼摆，自主探究 1. 出示情境：老师为每个小组都准备了学具，请同学们先打开学具袋看看 都有什么。（不同的小组学具是不同的，有锐角三角形、钝角三角形、 直角三角形、等腰直角三角形） 二、动手实践，深入探究 （一）借助拼摆，自主探究 2. 提出问题 ：你能根据已有的经验，借助手中的学具推导出三角形的面积 计算公式吗？ 3. 提出要求 ：请同学们 两人一组，借助你们手中的 三角形纸片 ，可以 拼一 拼， 画一画，剪一剪，看看能不能 把三角形转化成我们学习过的图形， 并 找到转化前后图形间的联系，把你找到的联系在纸上写一写，让别人 一眼就能看出你是如何推导出 三角形 面积计算方法的 ，看哪组的方法最 多，学具不够用可以找老师领取。 4. 学生自主探究，教师巡视搜集资源 。 二、动手实践，深入探究 （一）借助拼摆，自主探究 5. 暴露资源，组织研讨 ： 谁愿意说说你们是怎么想的？ 预设一： 底 高 底 高 平行四边形 的面积 ＝ 底 × 高 2 个三角形的 面积 底 高 三角形的 面积 ＝ 底 × 高 ÷ 2 二、动手实践，深入探究 （一）借助拼摆，自主探究 预设二： 底 高 底 高 5. 暴露资源，组织研讨 ： 谁愿意说说你们是怎么想的？ 平行四边形 的面积 ＝ 底 × 高 2 个三角形的 面积 底 高 三角形的 面积 ＝ 底 × 高 ÷ 2 二、动手实践，深入探究 （一）借助拼摆，自主探究 预设三： 底 高 底 高 平行四边形 的面积 ＝ 底 × 高 2 个三角形的 面积 底 高 三角形的 面积 ＝ 底 × 高 ÷ 2 5. 暴露资源，组织研讨 ： 谁愿意说说你们是怎么想的？ 二、动手实践，深入探究 （一）借助拼摆，自主探究 预设四： 底 高 底 高 5. 暴露资源，组织研讨 ： 谁愿意说说你们是怎么想的？ 平行四边形 的面积 ＝ 底 × 高 2 个三角形的 面积 底 高 三角形的 面积 ＝ 底 × 高 ÷ 2 二、动手实践，深入探究 （一）借助拼摆，自主探究 6. 总结概括，提升认识：通过同学们刚才的汇报，我们发现只要是两个 完全一样的三角形，我们就能把它们拼成一个平行四边形或长方形、 正方形，充分论证了 三角形的 面积 ＝ 底 × 高 ÷ 2 。 过渡：刚才我还发现有的同学只用一个三角形就推导出了三角形的面积 计算公式，你们想看看吗？ 二、动手实践，深入探究 （一）借助拼摆，自主探究 7. 暴露资源，组织研讨 ： 谁愿意说说你们是怎么想的？ 预设一： 底 高 平行四边形 的面积 ＝ 底 × 高 三角形的 面积 底 （ 高 ÷ 2 ） 三角形的 面积 ＝ 底 × 高 ÷ 2 二、动手实践，深入探究 （一）借助拼摆，自主探究 预设二： 底 高 平行四边形 的面积 ＝ 底 × 高 三角形的 面积 底 （ 高 ÷ 2 ） 三角形的 面积 ＝ 底 × 高 ÷ 2 7. 暴露资源，组织研讨 ： 谁愿意说说你们是怎么想的？ 二、动手实践，深入探究 （一）借助拼摆，自主探究 预设三： 底 高 平行四边形 的面积 ＝ 底 × 高 三角形的 面积 底 （ 高 ÷ 2 ） 三角形的 面积 ＝ 底 × 高 ÷ 2 7. 暴露资源，组织研讨 ： 谁愿意说说你们是怎么想的？ 二、动手实践，深入探究 （一）借助拼摆，自主探究 8. 总结概括，提升认识：通过同学们刚才的汇报，我们发现只要是运用 相应的方法把一个三角形割补或折叠后，我们就能把它们转化成一个 平行四边形或长方形，充分论证了 三角形的 面积 ＝ 底 × 高 ÷ 2 。 9. 出示字母公式：如果用 S 表示三角形的面积，用 a 表示三角形的底，用 h 表示三角形底边上的高，三角形的面积公式用字母怎样表示呢？ S ＝ ah ÷ 2 三、解决问题，提升认识 红领巾的底是 100 cm ，高 33 cm ，它的面积是多少平方厘米？ S ＝ ah ÷ 2 ＝ 100×33÷2 ＝ 1650 （ cm 2 ） 答：它的面积是 1650 cm 2 。 三、解决问题，提升认识 1. 一种三角尺的形状如下图，它的面积是多少？ S ＝ ah ÷ 2 ＝ 12.5×7.2÷2 ＝ 45 （ cm 2 ） 答：它的面积是 45 cm 2 。 三、解决问题，提升认识 2. 指出下面每个三角形的底和高，并分别计算出它们的面积。 S ＝ ah ÷ 2 ＝ 3×4÷2 ＝ 6 （ cm 2 ） 答：三个图形的面积分别为 6 cm 2 、 1.8 dm 2 、 3.5 m 2 。 S ＝ ah ÷ 2 ＝ 4×0.9÷2 ＝ 1.8 （ dm 2 ） S ＝ ah ÷ 2 ＝ 2.5×2.8÷2 ＝ 3.5 （ m 2 ） 回顾一下，今天我们是如何推导出了三角形的面积，还有什么问题吗？ 四、课堂小结 四、布置作业 作业：第 93 页练习二十，第 1 题、第 3 题。 第 94 页练习十二，第 6 题。