五年级上册数学教案-5组合图形的面积 ︳青岛版 (9) 12页

1 义务教育课程标准青岛版小学数学五年级上册第 5 单元 生活中的多边形 课 题 组合图形的面积（信息窗 4） 课型 新授 教 学 目 标 知识与技能 1．联系生活实际认识组合图形，会求组合图形的面积。 知道求组合图形的面积可以转化成求几个简单平面图形 的面积和或面积差进行计算。 过程与方法 2．在拼一拼、找一找、分一分的活动中, 感受组合图形 的面积计算方法是灵活多样的,提高学生的识图能力，分 析综合能力和空间想象能力。 3．引导学生利用“分割法”或“补形法”把组合图形分 解成学过的平面图形，体会画化繁为简和转化思想，培养 创新意识和动手实践能力。 情感态度 与价值观 4.能运用所学的知识，灵活解决生活中组合图形的实际问 题，感受数学与生活的联系，体验用数学知识解决生活问 题的乐趣。 教学重点 探索并掌握用“分割法”或“补形法”求组合图形面积的 计算方法。 教学难点 理解计算组合图形面积的多种计算方法，根据图形之间的 联系和相关的隐蔽条件，引导学生寻找最简单方法,实现 方法选择的最优化。 教学准备 教师：希沃课件、自主学习作业单、合作学习作业单 2 学生：卡纸、剪刀、直尺、胶带等 教 学 过 程 教 学 过 程 一、创设情境，导入新课 谈话：多媒体出示教材“虾池”形状情境图。 同学们，你看到了什么？能想到什么？想说些什么？与大家分享。 预设：学生可能会出现下面的回答： 生 1：这个虾池的形状不属于我们之前学过的简单平面几何图形，是一 个不规则五边形。 生 2：这个虾池的面积是多少平方米？ 师：你有什么办法可以计算这个虾池的面积吗？ 补充：生 3：根据这个五边形的特点，我可以把这个虾池分割成一个梯 形加一个长方形（2 种分法）。 生 4：我可以把这个三角形分成三个三角形。 生 5：根据这个五边形的特点，我可以把这个五边形补成一个长方形， 虾池的面积就可以用长方形的面积减去三角形的面积。 质疑：第五位同学的方法可行吗？生生评价，师生评价。 同学们的办法真不错，由几个简单图形拼出来的图形，就叫做组合 图形。这节课我们就来探究有关平面组合图形的面积计算。（板书：组 3 教 学 过 程 合图形的面积） 设计意图：用学生身边熟悉的事物引课，引导学生仔细观察情境图， 提取数学信息，发现并提出有价值的数学问题，激发学生参与学习的兴 趣。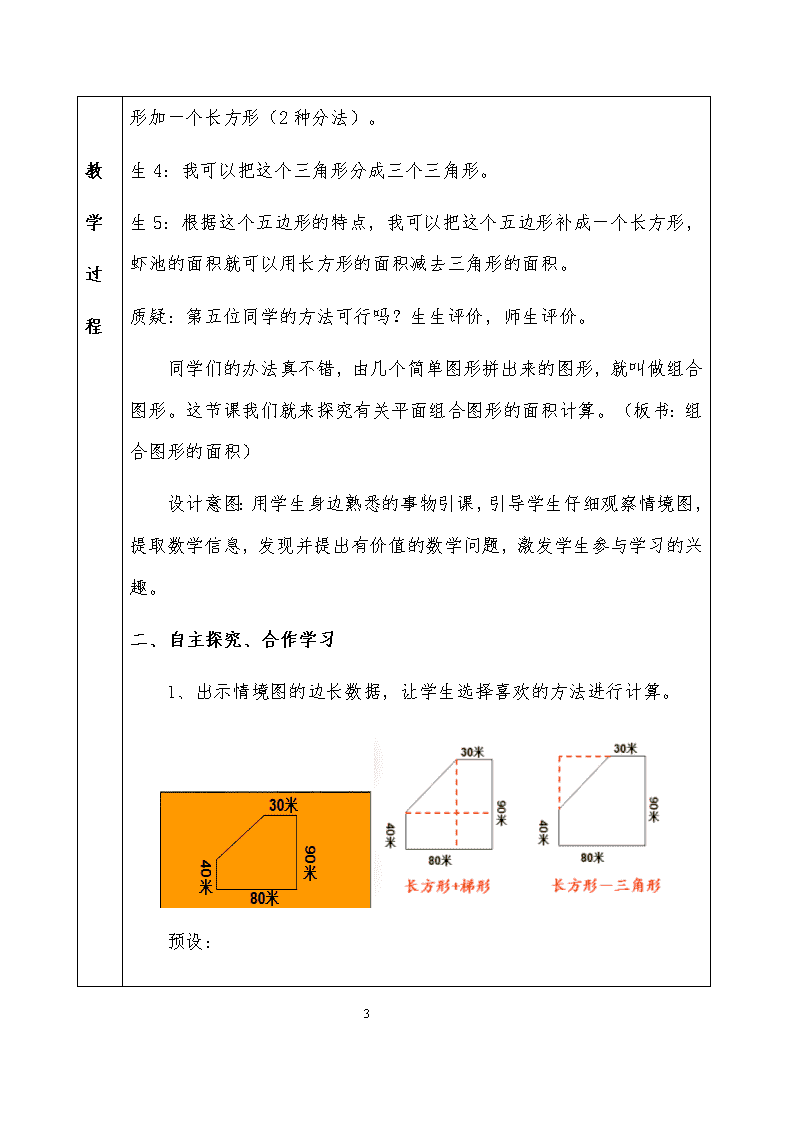 二、自主探究、合作学习 1、出示情境图的边长数据，让学生选择喜欢的方法进行计算。 预设： 方法一：作竖直辅助线 梯形+长方形 梯形：上底=40 米，下底=90 米，高=（80-30）=50 米； 长方形：长=90 米，宽=30 米 S=（40+90）×50÷2+90×30 =130×50÷2+2700 =3250+2700 =5950（平方米） 方法二：作水平辅助线 梯形+长方形 4 教 学 过 程 梯形：上底=30 米，下底=80 米，高=（90-40）=50 米； 长方形：长=80 米，宽=40 米 S=（30+80）×50÷2+80×40 =110×50÷2+3200 =2750+3200 =5950（平方米） 方法三：辅助线 长方形-三角形 三角形：底=（90-40）=50 米，高=（80-30）=50 米； 长方形：长=90 米，宽=80 米 S=90×80-50×50 =7200-2500 =5950（平方米） 点评：在计算之前，同学们的分割了不同的图形，为什么你们没有 用三个三角形的面积和，也没有用一个三角形加一个梯形的面积计算？ 预设：某些边或者高不知道，需要实际测量。 设计意图：独立思考是高年级学生必备的学习能力，课堂教学中教 师应该坚持培养学生独立思考和解决问题的习惯。初步掌握计算组合图 形面积的方法，并从解决问题的方法中学会选择最优的方法。在解决问 题过程中培养学生充分利用数学显性信息和隐蔽信息的能力。 2、师：请你说一说生活中那些物体可以抽象出组合图形？ 预设：桌子、凳子、防护栏、教学楼、足球场的球门…… 5 教 学 过 程 师：同学们说的非常好，老师早上进校园时也拍了几张照片，请同 学们看一下，有那些组合图形。下面请同学们以小组为单位合作学习（四 人小组） 1 小组合作学习要求：（限时 5 分钟） 2 （1）请你们小组合作，可以制作的简单几何图形，拼一拼看能 组成哪些组合图形，也可以制作常见的组合图形，想一想怎样 计算这些图形的面积？ 3 （2）计算组合图形的面积，在小组内讨论计算方法？ 4 （3）想一想：计算组合图形的面积需要经历哪几个步骤？有什 么需要注意的地方。 5 生探究教师巡视并进行必要的指导。 设计意图：先让学生自主探索，让他们尝试从生活中提取常见物体 的平面图，可能大部分是组合图形。老师不要急于要答案，给他们相互 交流的机会，调动学生学习的积极性，发展学生数学思维的广度和宽度。 3、汇报展示、补充质疑 教师引导：谁来汇报你们组拼的是生活中的什么图形，是怎样求这 个图形的面积的？ 让学生把作品贴在黑板上，利用希沃授课助手展示学生合作学习 单，学生对照学习单发言。（四五组） 预设第一小组： 6 教 学 过 程 梯形+长方形 梯形：上底=20cm，下底=10cm，高=4cm； 长方形：长=50cm，宽=35cm S=（20+10）×4÷2+50×35 =30×4÷2+1750 =60+1750 =1810（cm2） 生生补充质疑，生生互评。 预设第二小组： 方法一：长方形-大三角形 长方形：长=80cm，宽=60cm 大三角形：底=60cm，高=20cm 80×60-60×20÷2 =4800-600 7 教 学 过 程 =4200（cm2） 方法二：梯形×2 梯形：上底=（80-20）=60（cm），下底=80cm，高=60÷2=30（cm） 2×S=（80+60）×30÷2×2 =140×30÷2×2 =4200（cm2） 预设第三小组：（对第二小组进行方法补充） 方法三：正方形+三角形×2 正方形：边长=60cm 三角形：底=30cm，高=（80-60）=20（cm） 60×60+30×20÷2×2 =3600+600 =4200(cm2) 生生补充质疑，生生互评。 师：请同学们观察以上三种方法，你最喜欢哪一种方法？为什么？ 预设： 生 1：我最喜欢第一种，长方形和三角形的面积都很好计算，而且 分出的图形少。 生 2：我最喜欢第二种，从中间割开，正好是两个全等的梯形，计 算一个梯形的面积再乘 2 就可以很快算出中队旗的面积。 生 3：我最喜欢第三种方法，分割后是一个正方形和两个全等的三 角形，也很好计算。 8 师：老师尊重你们独到的见解，从大家的分享中，老师听到了两个 非常重要的词：分割和添补。说明在计算不规则图形的面积的时候，我 们又做了一些转化工作，将要计算图形的面积转化成了一些基本图形的 面积，你们能将复杂问题转化成一个个简单问题去解决，老师非常认同。 下面请第四小组同学上台汇报： 预设第四小组： 正方体：棱长=4cm 4×4×3 =16×3 =48（cm2） 预设质疑：三个面的面积大小不一样，为什么用一个面的面积城 3？ 生：正方体的六个面都是全等的正方形，所以看到的这三个面是抽 象图，实际大小相等。 师：咱们的展示汇报就先到这里，其他小组的小组长可以把你们制 作的图形也贴在黑板上，供大家课后交流。 设计意图：通过自主平图，发散学生思维，发展学生的空间观念， 培养学生的创新精神。让学生借助直尺在组合图上画一画，用添加辅助 9 线的方法找出尽可能多的解题方法，然后通过比较的方法让学生从中优 化出解题的最佳方法。给学生更多的展示发言机会，培养学生的分享精 神，让他们学快乐的数学。 点评、总结、提升： 现在大家回忆一下我们是怎样来计算组合图形的面积的？ 预设：把组合图形分成我们学过的平面图形，分别算出各个小图形 的面积之后再把面积加起来。 同学们说的很好，我们把一个组合图形分成几个小图形用的是“分 割”的方法进行图形的转化，好多求组合图形的面积时都用到这种方法。 预设：把组合图形再补上一快变成我们学过的平面图形，然后从大 图形的面积里去掉补上的那个小图形的面积，就得到原图形的面积。 这种方法也很好，这种方法用的是“补形”的方法把图形进行转化， 这种方法是在组合图形的外边补上一快，用大图形的面积减去小图形面 积就得到原图形的面积。 4、再次交流计算组合图形的面积经历的步骤：一割补图形；二寻 找条件，计算面积。 无论“割”或“补”，同学们都在图形上画了一些线，这些线能帮 助我们更好地分割图、添补图形，这些线需要借助尺子来画，辅助线一 般要画成虚线。（板书：辅助线）。 用割补法计算组合图形面积时要注意：（课件出示） 要根据图形的特点，确定是用“割”还是用“补”的方法，“割” 或“补”后的图形都应是规范图形，而且“割”或“补”的平面图形越 10 少越好，容易计算， “割”我们用加法算，“补”我们用减法计算。 （板书：割+，补-） 三、走进生活、解决问题 1．我找茬：图中空白部分的面积是阴影部分面积的 2 倍。 注意：学生的方法可能有多种，只要合理教师都要给予肯定。 2．眼明手快。计算红色线条围成区域的面积。 先让学生分析并进行交流，然后找出最简便的方法进行计算。 “割补”结合： 预设：红色线条围成部分的面积等于两个长方形的面积减去左上和 下方整个三角形的面积。 大长方形的面积=12.5×8=100（cm2） 11 小长方形的面积=2.5×4=10（cm2） 左上方三角形的面积=12.5×8÷2=50（cm2） 下方三角形的面积=（12.5+2.5）×4÷2 =15×4÷2 =30（cm2） 红色线条围成部分的面积=100+10-50-30=30（cm2） 3、直通生活。学校要漆 20 扇教室门的正面，每平方米需要油漆 500g，一共需要油漆多少千克？ 先让学生观察每一面门的平面示意图，再说一说怎样求出每一面门 的面积。（如果课堂展示环节用时较长，本题让学生带出课堂完成） 预设列式：0.8×2-0.3×0.4 四、课堂小结 一起谈谈通过这节课的学习，你有什么收获？ 板 12 书 设 计 组合图形的面积 组合图形 基本图形 （辅助线）转化 割 + 补 - 教 学 反 思 1.教学反思：回看课堂，我感觉亮点之处有： (1) 让学生借助直尺在组合图上画一画，用添加辅助线的方法找出 解题方法。 在本节课教学中，学生的思维训练贯穿整堂课，在创设问题情境和 小组合作学习环节，让学生借助直尺在组合图上画一画，用添加辅助线 的方法找出尽可能多的解题方法，然后通过比较的方法让学生从中优化 出解题的最佳方法。 (2)出现未预想到的“正方体”的正视图。 学生的想法很奇特，是预料之外的。虽然学生对三个面的大小产生 了疑惑，但是也合情合理的解释了乘 3 的原因。 小组合作、展示汇报的取舍 1. 小组合作的成果课堂上不可能全部展示，根据课堂实际情况有 选择的展示。 2. 在学生探究时一定要给学生充足的探索时间和机会，让每个学 生都参与到活动中来，尽最大限度地发展学生的观察思考能力和探究能 力。