五年级上册数学教案-4简易方程（方程）▏沪教版 (4) 5页

‎ ‎ 教学设计方案 课题 方程 教师 日期 一. 教学目标：‎ ‎1. 结合具体情境，理解方程的含义，在判断、辨析中感悟方程的本质特征，并会用方程表示简单情境中的等量关系。‎ ‎2. 通过观察、比较、分析，经历从具体生活情境中寻找等量关系并用数学语言表达，再到用含有未知数的等式表示等量关系的过程。‎ ‎3. 初步体会方程的作用并产生学习方程的愿望，认识数学抽象的作用。‎ 教学重难点：理解方程的意义。‎ 二．制定依据：‎ ‎（一）教材分析 ‎“方程的初步认识”是沪教版《数学》五年级上册第四单元的教学内容，这部分教学内容是学生在认识了用字母表示数，求值、化简的基础上进行的，在此过程中渗透了符号思想。教材从整体上以直观、形象的素材呈现，让学生能较为清晰地理解等式，继而在天平的引导下感知“方程”的真正含义。整个学习过程，学生在经历观察、抽象、概括的过程中逐步构建“方程”这一完整的知识结构。‎ ‎（二）学情分析 学生在之前四年的数学学习中只接触到具体的数的运算，而对代数中的方程思想毫无概念，是一个崭新的领域。对于“方程”，学生感到既新鲜又陌生，很多学生对其有着很强的期待感。如何让学生在借助天平的教学引导过程中习得新知，以使学生有质疑、有冲突，从而更深层次地构建完整的知识结构？在设计本课时，围绕一条主线（建立等量关系）贯穿教学的始终，不仅使学生了解方程的外部特征，更重要的是理解方程的本质内涵，即为了求解未知数，在未知数与已知数之间建立等量关系。‎ 教学过程 教学环节 对应目标 教师活动 学生活动 设计意图 及评价关注点 情境引入 自由回答 - 5 -‎ ‎ ‎ ‎1、根据他们的对话，谁的年龄已知，谁的年龄未知？‎ ‎2、是不是有关系就能求出这些未知的年龄了呢？‎ 认识已知数和未知数。‎ 比较辨析，初步感知 对应目标：1，2‎ 对应目标：2，3‎ ‎（一）感悟方程的本质特征 ‎1、再次阅读，能根据信息确定这些未知年龄吗？‎ 妈妈：我的年龄减去20岁，还比你的年龄大。‎ 爸爸：我的年龄减去30岁，要比你的年龄小。‎ 李叔叔：我的年龄减去25岁，和你的年龄相等。‎ 张阿姨：我的年龄除以3，正好是你的年龄。‎ ‎2、同样给出了关系信息，为什么妈妈爸爸的年龄不能确定，叔叔阿姨的年龄却可以了呢？‎ ‎3、数学上我们把这种相等的关系，称为是“等量关系”。（板书）‎ 小结：刚刚给出的四条信息都是在反映各自年龄和小胖年龄之间的关系，但只有反映等量关系的信息才能求出未知数。‎ ‎（二）感悟方程的形式特征 ‎1、如果这里的每一句话都用一个含有字母的式子表示出来，你能发现表示等量关系的式子有什么特征吗？‎ a-20＞10 b-30＜10 x-25=10 y÷3=10‎ 自由回答 独立思考 个别回答 记录 依据不同数学信息，比较、辨析，初步感悟方程的本质特征。‎ 比较、辨析四个字母表达式，初步感悟方程的形式特征。‎ 评价关注点：学生能否通过比较分析，较为 - 5 -‎ ‎ ‎ ‎2、为了求出未知数，在未知数和已知数之间建立起等量关系。那么像这样含有未知数的等式就叫做方程。（揭示课题）‎ ‎3、判断a-20＞10 b-30＜10是不是方程。‎ 小结：方程是在未知数和已知数之间建立起的等量关系式，也就是一个含有未知数的等式。‎ 个别回答 清晰地表达三组信息之间以及三个字母表达式之间的区别。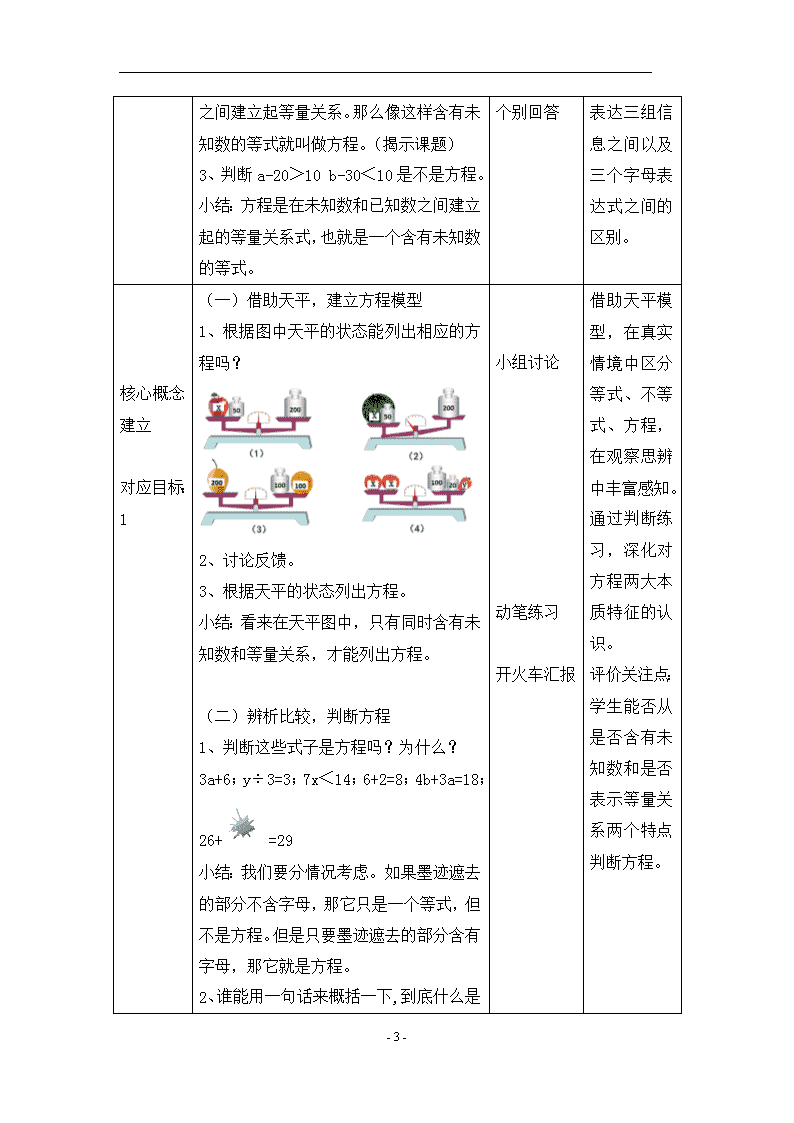‎ 核心概念建立 对应目标：1‎ ‎（一）借助天平，建立方程模型 ‎1、根据图中天平的状态能列出相应的方程吗？‎ ‎2、讨论反馈。‎ ‎3、根据天平的状态列出方程。‎ 小结：看来在天平图中，只有同时含有未知数和等量关系，才能列出方程。‎ ‎（二）辨析比较，判断方程 ‎1、判断这些式子是方程吗？为什么？‎ ‎3a+6；y÷3=3；7x＜14；6+2=8；4b+3a=18； ‎ ‎26+=29‎ 小结：我们要分情况考虑。如果墨迹遮去的部分不含字母，那它只是一个等式，但不是方程。但是只要墨迹遮去的部分含有字母，那它就是方程。‎ ‎2、谁能用一句话来概括一下,到底 小组讨论 动笔练习 开火车汇报 借助天平模型，在真实情境中区分等式、不等式、方程，在观察思辨中丰富感知。‎ 通过判断练习，深化对方程两大本质特征的认识。‎ 评价关注点：学生能否从是否含有未知数和是否表示等量关系两个特点判断方程。‎ - 5 -‎ ‎ ‎ 什么是方程？‎ 小结：为了求解未知数，在未知数和已知数之间建立的等量关系式就是方程。‎ 练习巩固 对应目标：1,3‎ ‎1、看图列方程。‎ ‎（1)说一说背后的等量关系？‎ ‎（2）仔细观察这四个方程，谁最不一样？‎ 小结：这就是我们以前的算法呀，通过已知数的运算，直接求出未知数。这时一般就不再需要用字母表示了。而通过今天的学习，我们知道了求未知数还可以用这样的式子表示，也就是方程。‎ ‎2、能用4a=300来描述的情境是（ ）‎ ‎（1）4，a分别表示，等量关系是？‎ ‎（2）小结：在这儿三个情境虽然各不相同，但他们背后隐藏的意义都是一样的。一个方程就可以顶天下。‎ ‎（3）你还能不能到生活中再找一个情境，也能用4a=300来表示的吗？‎ 个别回答 动笔练习 手势表示 小组讨论 感受等量关系不仅仅出现在平衡的天平上，还可以有不同的表现形式。‎ 认识方程是刻画现实世界中等量关系的有效数学模型。‎ 评价关注点：学生能否根据简单情景图列出方程，并说出背后的等量关系。‎ 全课小结 对应目标：3‎ ‎1、方程的历史。‎ ‎2、这节课你有什么收获？‎ 观看课件 作业设计：练习册P58‎ 板书设计： 等量关系 方程 ‎ ‎ 未知数 已知数 ‎ ‎ 含有未知数的等式 ‎ x-25=10‎ ‎ y÷3=10‎ ‎ x+50=200 ‎ ‎ x+x=100+20+y ‎ - 5 -‎ ‎ ‎ 反思重建：‎ - 5 -‎