人教版小学六年级下册数学课件第六单元整理和复习课时 19页

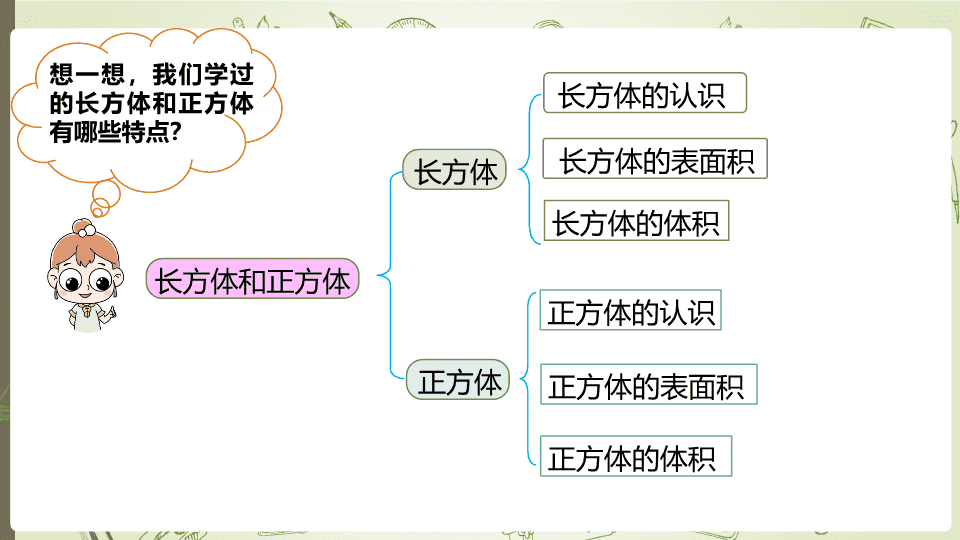
整理和复习 第13课时 图形与几何 【重点】分析、归纳长方体、正方体表面积和体积计算公式间的内在联 系。理解三视图及正方体、长方体的特点。 【难点】运用所学的知识解决生活中的实际问题。 1．使学生认识长方体、正方体、知道它们的特点。 2．复习长方体、正方体体积的计算公式，加深学生对立体图形的认识， 使学生对所学的知识进一步系统化和概括化。 3．使学生在解决实际问题中，感受数学与生活的密切联系，加强数学知 识与日常生活的联系，发展学生的空间观念。 想一想，我们学过 的长方体和正方体 有哪些特点？ 长方体和正方体 长方体 正方体 长方体的认识 长方体的表面积 长方体的体积 正方体的认识 正方体的表面积 正方体的体积 长方体和正方体的认识 长方体认识 下面这些立体图形 各有什么特点？ 面 有6个面，每个面一般是长方形，特殊两个 面是正方形。相对两个面的面积相等。 有12条棱，相对的四条棱互相平行且相等。棱 棱长和=(长+宽+高)×4 有8个顶点。顶点 正方体认识 下面这些立体图形 各有什么特点？ 面 有6个面，每个面都是正方形，每个面面积都相等。 有12条棱，每条棱长度都相等。棱 棱长和=棱长×12 有8个顶点。顶点 长方体与正方体分别有 什么相同点和不同点？ 长方体和正方体的认识 相同点 不同点 立体图形 面 棱 点 面的形状 面积 棱长 关系 长方体 6个 12条 8个 6个面一般是长方形， 也有可能有两个相对 的面是正方形 相对的面 的面积相 等 每一组互 相平行的 四条棱长 相等 正方体是 特殊的长 方体 正方体 6个面都是相等的正 方形 6 个 面 的 面积都相 等 1 2 条 棱 的长度都 相等 长方体与正方体的相同点与不同点 长方体的表面积 长方体和正方体的表面积 表面积就是物体外表面所有面积的和。 长方体的表面积是 6个面的面积和。 上 下 后 前左 右 长×高 长×宽 宽×高 表面积=(长×宽+长×高+宽×高)×2 长方体相对面的面积相等。 正方体的表面积 长方体和正方体的表面积 表面积就是物体外表面所有面积的和。 正方体的表面积是 6个面的面积和。 上 下 后 前 左 右 正方体6个面都是相 等的正方形。 表面积=棱长×棱长×6 体积是物体所占空间的大小。 长方体的体积=长×宽×高 正方体的体积=棱长×棱长×棱长 长方体和正方体的体积=底面积×高 V = Sh 常用的体积单位有 cm³、dm³、m³。 观察下面用4个正方体搭成的图形，并填一填。 ① ② ③ ④ ⑤ (1)从正面看到的图形是 的有（ ）。 (2)从侧面看到的图形是 的有（ ）。 (3)从上面看到的图形是 的有 （ ）。 ① ④ ③ ② ⑤ 下面哪些图形沿虚线折叠后能围成长方体。 √ √ × √ 首先找两个相对且相等的 面，切记相隔一个面。 解决问题。 把一个棱长是1.2米的正方体铁箱油漆一遍，(内外两面)油漆部分 的面积是多少平方米？ 1.2×1.2×6× 2 =1.44×6×2 =17.28(平方米)答：油漆部分的面积是17.28平方米。 先求正方体的表 面积再乘2。 解决问题。 把一根长3米的长方体木料锯成3段后，表面积增加18平方 分米，这根木料原来的体积是多少立方分米？ 18÷4 =4.5×3 =13.5(立方分米) 增加4个长方体 底面的面积。 答：这根木料原来的体积是13.5立方分米。 长方体体积=底面积×高 × 3 一块长40厘米，宽30厘米的长方形铁皮，把它的四个角分别切掉 边长为4厘米的正方形，然后焊接成一个无盖的盒子。它的容积 是多少升？ 长方体的长和宽 各减少8厘米。 40-4-4=32(厘米) 30-4-4=22(厘米) 32×22×4=2816(立方厘米) 2816立方厘米=2.816立方分米=2.816升 答：它的容积是2.816升。 长方体的高是4厘米， 容积=长×宽×高。 解决问题。 1 填空。 1、一本数学书的体积大约是320( )，表面积大约是 400( )。 2、一节集装箱所占空间约是60( )。 3、3.05立方米=( )立方分米 4、4560立方分米=( )升 相邻体积单位之间的进率是1000 立方厘米 立方米 平方厘米 3050 4560 2 判断，对的在括号里打“√”，错的答“×”。 容积和体积的意义不同。 ×1、一个木箱的体积就是它的容积。( ) 2、长方体是特殊的正方体。( ) 3、棱长6分米的正方体，它的表面积和体积相等。( ) 4、用4个棱长为1厘米的小正方体可以拼成一个大正方体。 ( ) × × × 用8个 3 解决问题。 一个长方体容器，底面长3分米，宽1.6分米，放入一块石头(完全侵入) 后水面上升了0.7分米，这块石头的体积是多少？ 体积=底面积×高 3×1.6×0.7 =4.8×0.7 =3.36(立方分米) 答：这块石头的体积是3.36立方分米。 4 解决问题。 把一个棱长6分米的正方体钢块，锻造成横截面积为4平方厘米的 长方体钢材，这根钢材长多少米？ 先求正方体钢块的体积 6×6×6=216 (立方分米) 4平方厘米=0.0004平方米 0.216÷0.0004=540 (米) 216立方分米=0.216立方米 答：这根钢材长540米。 5 在方格纸上画出从不同方向看到左边立体图形的形状图。 正面 正面就是从前面。 左面 上面