2020年山东省济南市小升初小学数学压轴题预测试卷2【含答案及详细解释、可编辑】 11页

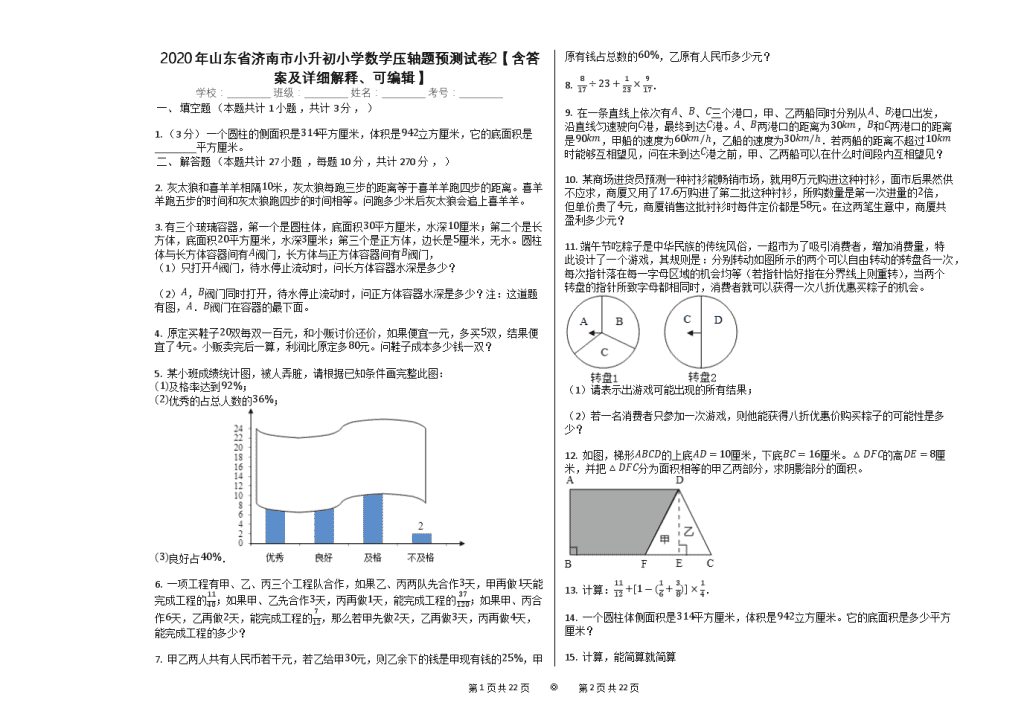
‎2020年山东省济南市小升初小学数学压轴题预测试卷2【含答案及详细解释、可编辑】‎ 学校：__________ 班级：__________ 姓名：__________ 考号：__________‎ ‎ 一、 填空题 （本题共计 1 小题 ，共计3分 ， ） ‎ ‎ ‎ ‎1. （3分） 一个圆柱的侧面积是‎314‎平方厘米，体积是‎942‎立方厘米，它的底面积是________平方厘米。 ‎ ‎ 二、 解答题 （本题共计 27 小题 ，每题 10 分 ，共计270分 ， ） ‎ ‎ ‎ ‎2. 灰太狼和喜羊羊相隔‎10‎米，灰太狼每跑三步的距离等于喜羊羊跑四步的距离。喜羊羊跑五步的时间和灰太狼跑四步的时间相等。问跑多少米后灰太狼会追上喜羊羊。 ‎ ‎ ‎ ‎3. 有三个玻璃容器，第一个是圆柱体，底面积‎30‎平方厘米，水深‎10‎厘米；第二个是长方体，底面积‎20‎平方厘米，水深‎3‎厘米；第三个是正方体，边长是‎5‎厘米，无水。圆柱体与长方体容器间有A阀门，长方体与正方体容器间有B阀门， ‎ ‎（1）只打开A阀门，待水停止流动时，问长方体容器水深是多少？‎ ‎ ‎ ‎（2）A，B阀门同时打开，待水停止流动时，问正方体容器水深是多少？注：这道题有图，A．B阀门在容器的最下面。‎ ‎ ‎ ‎4. 原定买鞋子‎20‎双每双一百元，和小贩讨价还价，如果便宜一元，多买‎5‎双，结果便宜了‎4‎元。小贩卖完后一算，利润比原定多‎80‎元。问鞋子成本多少钱一双？ ‎ ‎ ‎ ‎5. 某小班成绩统计图，被人弄脏，请根据已知条件画完整此图： ‎(1)‎及格率达到‎92%‎； ‎(2)‎优秀的占总人数的‎36%‎； ‎(3)‎良好占‎40%‎． ‎ ‎ ‎ ‎6. 一项工程有甲、乙、丙三个工程队合作，如果乙、丙两队先合作‎3‎天，甲再做‎1‎天能完成工程的‎11‎‎40‎；如果甲、乙先合作‎3‎天，丙再做‎1‎天，能完成工程的‎37‎‎120‎；如果甲、丙合作‎6‎天，乙再做‎2‎天，能完成工程的‎7‎‎12‎，那么若甲先做‎2‎天，乙再做‎3‎天，丙再做‎4‎天，能完成工程的多少？ ‎ ‎ ‎ ‎7. 甲乙两人共有人民币若干元，若乙给甲‎30‎元，则乙余下的钱是甲现有钱的‎25%‎，甲原有钱占总数的‎60%‎，乙原有人民币多少元？ ‎ ‎ ‎ ‎8. ‎8‎‎17‎‎÷23+‎1‎‎23‎×‎‎9‎‎17‎． ‎ ‎ ‎ ‎9. 在一条直线上依次有A、B、C三个港口，甲、乙两船同时分别从A、B港口出发，沿直线匀速驶向C港，最终到达C港。A、B两港口的距离为‎30km，B和C两港口的距离是‎90km，甲船的速度为‎60km/h，乙船的速度为‎30km/h．若两船的距离不超过‎10km时能够互相望见，问在未到达C港之前，甲、乙两船可以在什么时间段内互相望见？ ‎ ‎ ‎ ‎10. 某商场进货员预测一种衬衫能畅销市场，就用‎8‎万元购进这种衬衫，面市后果然供不应求，商厦又用了‎17.6‎万购进了第二批这种衬衫，所购数量是第一次进量的‎2‎倍，但单价贵了‎4‎元，商厦销售这批衬衫时每件定价都是‎58‎元。在这两笔生意中，商厦共盈利多少元？ ‎ ‎ ‎ ‎11. 端午节吃粽子是中华民族的传统风俗，一超市为了吸引消费者，增加消费量，特此设计了一个游戏，其规则是：分别转动如图所示的两个可以自由转动的转盘各一次，每次指针落在每一字母区域的机会均等（若指针恰好指在分界线上则重转），当两个转盘的指针所致字母都相同时，消费者就可以获得一次八折优惠买粽子的机会。 ‎ ‎（1）请表示出游戏可能出现的所有结果；‎ ‎ ‎ ‎（2）若一名消费者只参加一次游戏，则他能获得八折优惠价购买粽子的可能性是多少？‎ ‎ ‎ ‎12. 如图，梯形ABCD的上底AD=10‎厘米，下底BC=16‎厘米。‎△DFC的高DE=8‎厘米，并把‎△DFC分为面积相等的甲乙两部分，求阴影部分的面积。 ‎ ‎ ‎ ‎13. 计算：‎11‎‎12‎‎+[1-(‎1‎‎6‎+‎3‎‎8‎)]×‎‎1‎‎4‎． ‎ ‎ ‎ ‎14. 一个圆柱体侧面积是‎314‎平方厘米，体积是‎942‎立方厘米。它的底面积是多少平方厘米？ ‎ ‎ ‎ ‎15. 计算，能简算就简算 ‎ 第21页 共22页 ◎ 第22页 共22页 ‎8‎‎17‎‎÷23+‎1‎‎23‎×‎‎9‎‎17‎‎． ‎ ‎ ‎ ‎16. 在沿铁路的公路上，甲乙两汽车同时从A站向B站行驶。甲车每小时行‎30‎千米，乙车每小时行‎45‎千米，两车同时出发半小时后，一辆列车也从A站向B站行驶，列车行驶一定时间后分别赶上了两车。列车从追上甲车到完全超过甲车用了‎9‎秒钟，从追上乙车到完全超过乙车用了‎12‎秒钟。当列车完全超过乙车时，列车离开A站多远？ ‎ ‎ ‎ ‎17. 有甲乙两个木匠师傅，甲师傅一天能做‎3‎张桌子或‎9‎把椅子，乙师傅每天能做‎2‎张桌子或‎7‎把椅子，甲乙两人合作，‎20‎天做了桌子和椅子共‎134‎张，问：做了几张桌子，几把椅子？ ‎ ‎ ‎ ‎18. 将一个长方形的长减少‎3‎厘米，宽增加‎2‎厘米，就得到一个与原来的这个长方形面积相等的正方形，原来长方形的面积是多少平方厘米？ ‎ ‎ ‎ ‎19. 某商人以每件‎120‎元的价格卖出了两件衣服，发现一件赔了‎20%‎，一件赚了‎20%‎，这个商人赔了还是赚了？若赔了，赔了多少钱？若赚了，赚了多少钱？ ‎ ‎ ‎ ‎20. ‎20÷[63×(‎5‎‎7‎-‎5‎‎9‎)×‎2‎‎5‎]‎． ‎ ‎ ‎ ‎21. 如图是十字道路，甲车在东西路上，由东向西行进，乙车在南北路上，由北向南行进。甲出发点在交叉点东‎350‎米的位置上，乙出发点在交叉点上。两车同时出发，‎10‎秒钟后，甲、乙两车所在的位置距交叉点的路程相等（这时甲仍在交叉点东）．再经过‎60‎秒，两车所在的位置又距交叉点路程相等（这时甲在交叉点西）．求甲乙两车每秒各行多少米？ ‎ ‎ ‎ ‎22. 如图，一个边长为‎40‎厘米的正方形ABCD的场地，蚂蚁和蜗牛同时从A点出发，蚂蚁以‎5‎厘米/分钟的速度沿线路A→B→C→D行走，蜗牛以‎2‎厘米/分钟的速度沿线路A→D行走。出发‎18‎分钟时，蚂蚁走到E点，蜗牛走到F点，求三角形AEF的面积是多少平方厘米？ ‎ ‎ ‎ ‎23. 小莉家的文具店正热卖贴画，一种‎1‎元钱‎3‎张，另一种‎1‎元钱‎2‎张。周末小莉帮妈妈卖贴画，她将两种贴画混在一起按‎2‎元钱‎5‎张来卖。请通过计算说明：同样将两种贴画各卖出‎30‎张，小莉的卖法和原来妈妈的卖法哪一种挣钱多？ ‎ ‎ ‎ ‎24. 某市供水公司为鼓励居民节约用水，规定：每户每月用水不超过‎22‎立方米时，按每立方米‎1.8‎元收费；超过‎22‎立方米的部分按每立方米‎3‎元收费。李明家上月用水‎25‎立方米，请你算一算李明家上月消费多少元？ ‎ ‎ ‎ ‎25. 把一个长‎7‎厘米，宽‎6‎厘米，高‎4.5‎厘米的长方体铁块和一个棱长‎5‎厘米的正方体的铁块，熔铸成一个大圆柱体，这个圆柱体的底面积是‎78.5‎平方厘米，那圆柱的高应是多少厘米？ ‎ ‎ ‎ ‎26. 把一个直径是‎2‎分米的圆柱的底面分成许多相等的扇形，然后沿直径把圆切开，拼成一个和它体积相等的长方体，这个长方体表面积比原来圆柱的表面积增加‎8‎平方分米，这个长方体的体积是多少？ ‎ ‎ ‎ ‎27. 体育场买来‎16‎个篮球和‎12‎个足球，共付出‎760‎元。已知篮球与足球的单价比是‎5:6‎，体育场买篮球和足球各付出多少元？ ‎ ‎ ‎ ‎28. 某机关精简后有工作人员‎75‎人，比原来少‎45‎人，精简了百分之几？（提示：想想清楚精简百分之几是指谁是谁的百分之几？） ‎ ‎ 三、 应用题 （本题共计 12 小题 ，每题 15 分 ，共计180分 ， ） ‎ ‎ ‎ ‎29. 一个自行车队进行训练，训练时所有的队员都以‎35‎千米/时的速度前进，突然，‎1‎号队员以‎45‎千米/时的速度独自行进，行进‎10‎千米后调转车头，仍以‎45‎千米/时的速度往回骑，直到与其他队员会合，‎1‎号队员从离队开始到与队员重新会合，经历了多长时间？ ‎ ‎ ‎ ‎30. 某商品成本价为每件‎500‎元，‎3‎月份的销售价为每件‎625‎元。经市场预测，该商品销售价将在‎4‎月份降低‎20%‎，而在‎5‎月份再提高‎8%‎，那么在‎5‎月份销售该商品预计可达到的利润率为多少？ ‎ ‎ ‎ ‎31. 一件工程，甲单独做需‎20‎天完成，乙单独做需‎12‎天完成。这样工作先由甲做了若干天，然后由乙继续做完，从开始到完工共用‎14‎天。这样工作由甲先做了几天？ ‎ ‎ ‎ ‎32. 一个圆锥形小麦堆，底面半径是‎2‎米，高‎3‎米。如果每立方米小麦大约重‎750‎千克，这堆小麦约重多少千克？ ‎ ‎ ‎ ‎33. 两地相距‎90‎千米，甲、乙两辆汽车同时从两地相向开出，‎2‎‎3‎小时相遇。甲、乙两车的速度比是‎4:5‎，甲、乙两车每小时各行多少千米？ ‎ ‎ ‎ ‎34. 小明调查了本地区四月份每天的天气情况，并统计了晴天、多云、阴天和雨天等各种天气的天数，制成了如图的统计图。 ‎ 第21页 共22页 ◎ 第22页 共22页 ‎ ‎ ‎（1）如果雨天的天数正好等于多云、阴天天数的和，那么这个地区四月份的雨天有多少天？‎ ‎ ‎ ‎（2）晴天的天数占这个月总天数的百分之几？是多少天？‎ ‎ ‎ ‎35. 某商店购进一批鞋子，每双售出价比购进价多‎15%‎．如果全部卖出，则可获利‎120‎元；如果只卖‎80‎双，还差‎64‎元才够成本。鞋子的购进价每双多少元？ ‎ ‎ ‎ ‎36. 加工一批零件，甲乙合作‎5‎小时完成，甲独做‎9‎小时完成。已知甲每小时比乙多加工‎2‎个零件，这批零件共有多少个？ ‎ ‎ ‎ ‎37. 某厂生产一批水泥，原计划每天生产‎150‎吨，可以按时完成任务。实际每天增产‎30‎吨，结果只用‎25‎天就完成了任务。原计划完成生产任务需要多少天？ ‎ ‎ ‎ ‎38. 压路机的滚筒是一个圆柱体。滚筒直径‎1.2‎米，长‎1.5‎米。现在滚筒向前滚动‎120‎周，被压路面的面积是多少？‎(π取‎3.14)‎ ‎ ‎ ‎ ‎39. 甲乙两地相距‎405‎千米，一辆汽车从甲地开往乙地，‎4‎小时行驶了‎180‎千米。照这样的速度，再行驶多少小时，这辆汽车就可以到达乙地？ ‎ ‎ ‎ ‎40. 一件工程，甲单独做要‎12‎小时完成，乙单独做要‎18‎小时完成。如果先由甲工作‎1‎小时，然后由乙接替甲工作‎1‎小时，再由甲接替乙工作‎1‎小时，…两人如此交替工作，那么完成任务时共用了多少小时？ ‎ 第21页 共22页 ◎ 第22页 共22页 参考答案与试题解析 ‎2020年山东省济南市小升初小学数学压轴题预测试卷2【含答案及详细解释、可编辑】‎ 一、 填空题 （本题共计 1 小题 ，共计3分 ） ‎ ‎1.【答案】‎ ‎36π ‎【解答】‎ 设底面半径为r，高为h，依题意得： πr‎2‎h＝‎942‎； ‎2πrh＝‎314‎； 两式相除，得r＝‎6‎； 所以，底面积S＝πr‎2‎＝‎36π；‎ 二、 解答题 （本题共计 27 小题 ，每题 10 分 ，共计270分 ） ‎ ‎2.【答案】‎ 跑‎160‎米后灰太狼会追上喜羊羊。‎ ‎【解答】‎ 解：根据题目条件有，灰太狼每跑‎3‎步的距离‎=‎喜羊羊跑‎4‎步的距离，所以灰太狼每跑‎1‎步的距离‎=‎喜羊羊跑‎4‎‎3‎步的距离。因为喜羊羊跑‎5‎步的时间‎=‎灰太狼跑‎4‎步的时间，知道灰太狼跑‎1‎步的时间‎=‎喜洋洋跑‎5‎‎4‎步的时间，由此可以求出灰太狼的速度：喜洋洋的速度‎=‎4‎‎3‎:‎5‎‎4‎=‎‎16‎‎15‎， 设跑x上米后灰太狼会追上喜羊羊， x：‎(x-10)=16:15‎，    ‎16x-160=15x，          x=160‎， ‎ ‎3.【答案】‎ 设打开A阀门，待水停止流动时长方体内水深‎7.2‎米；‎ ‎（2）设A，B阀门同时打开，待水停止流动时正方体容器水深是y米， ‎30y+20y+5×5y=360 ‎ ‎30y+20y+25y=360‎，         ‎75y=360‎，           y=4.8‎ 答：A，B阀门同时打开，待水停止流动时，正方体容器水深是‎4.8‎米。‎ ‎【解答】‎ 解：水的总体积为：‎30×10+20×3‎ ‎=300+60‎， ‎=360‎（立方厘米），（1）设打开A阀门，待水停止流动时长方体内水深x米， ‎30x+20x=360 ‎   ‎50x=360‎，      x=7.2‎， 答：设打开A阀门，待水停止流动时长方体内水深‎7.2‎米；‎ ‎（2）设A，B阀门同时打开，待水停止流动时正方体容器水深是y米， ‎30y+20y+5×5y=360 ‎ ‎30y+20y+25y=360‎，         ‎75y=360‎，           y=4.8‎ 答：A，B阀门同时打开，待水停止流动时，正方体容器水深是‎4.8‎米。‎ ‎4.【答案】‎ 鞋子成本‎88‎元钱一双。‎ ‎【解答】‎ 解：设原来的利润为x元，由题意得： ‎(x-4)×(20+5×4)-20x=80‎，   ‎(x-4)×(20+20)-20x=80‎，         ‎(x-4)×40-20x=80‎，              ‎40x-160-20x=80‎，                 ‎20x-160=80‎，             ‎20x-160+160=80+160‎，                     ‎20x=240‎，               ‎20x÷20=240÷20‎，                     x=12‎； 所以成本是：‎100-12=88‎（元）； ‎ ‎5.【答案】‎ 解：全班参加考试的人数为：‎2÷(1-92%)=25‎（人）， 及格的人数有：‎25×92%=23‎（人）， 优秀的人数有：‎25×36%=9‎（人）， 良好的人数有：‎25×40%=10‎（人）， 作图如下： ‎ ‎【解答】‎ 解：全班参加考试的人数为：‎2÷(1-92%)=25‎（人）， 及格的人数有：‎25×92%=23‎（人）， 优秀的人数有：‎25×36%=9‎（人）， 良好的人数有：‎25×40%=10‎（人）， 作图如下： ‎ 第21页 共22页 ◎ 第22页 共22页 ‎6.【答案】‎ 能完成工程的‎43‎‎120‎．‎ ‎【解答】‎ 解：‎(1)3‎乙‎+3‎丙+甲‎=‎‎11‎‎40‎ ‎(2)3‎甲‎+3‎乙+丙‎=‎‎37‎‎120‎ ‎(3)6‎甲‎+6‎丙‎+2‎乙‎=‎‎7‎‎12‎ ‎(1)(2)(3)‎相加可得：‎(4)‎甲+乙+丙‎=‎‎1‎‎8‎ ‎(2)-(1)‎可得‎(5)‎：甲‎=‎丙‎+‎‎1‎‎60‎ ‎(2)-(3)‎可得‎(6)‎：乙‎=‎丙‎+‎‎1‎‎120‎ 把‎(5)(6)‎代入‎(4)‎可得：‎3‎丙‎+‎1‎‎40‎=‎‎1‎‎8‎ 丙的工作效率： ‎(‎1‎‎8‎-‎1‎‎40‎)÷3 ‎‎=‎1‎‎10‎÷3 ‎‎=‎1‎‎30‎ ‎甲的工作效率： ‎1‎‎30‎‎+‎1‎‎60‎=‎1‎‎20‎ ‎乙的工作效率： ‎‎1‎‎30‎‎+‎1‎‎120‎=‎1‎‎24‎ ‎‎1‎‎20‎‎×2+‎1‎‎24‎×3+‎1‎‎30‎×4 ‎‎=‎1‎‎10‎+‎1‎‎8‎+‎2‎‎15‎ ‎‎=‎43‎‎120‎ ‎ ‎7.【答案】‎ 乙原有人民币‎60‎元。‎ ‎【解答】‎ 解：现有钱的‎25%‎，即乙的钱数是甲的‎1‎‎4‎， ‎30÷(‎4‎‎1+4‎-60%)×(1-60%) =30÷(‎4‎‎5‎-‎3‎‎5‎)×40%‎， ‎=30÷‎1‎‎5‎×40%‎， ‎=60‎（元）． ‎ ‎8.【答案】‎ 解：‎8‎‎17‎‎÷23+‎1‎‎23‎×‎‎9‎‎17‎， ‎=‎8‎‎17‎×‎1‎‎23‎+‎1‎‎23‎×‎‎9‎‎17‎， ‎=(‎8‎‎17‎+‎9‎‎17‎)×‎‎1‎‎23‎， ‎=1×‎‎1‎‎23‎， ‎=‎‎1‎‎23‎．‎ ‎【解答】‎ 解：‎8‎‎17‎‎÷23+‎1‎‎23‎×‎‎9‎‎17‎， ‎=‎8‎‎17‎×‎1‎‎23‎+‎1‎‎23‎×‎‎9‎‎17‎， ‎=(‎8‎‎17‎+‎9‎‎17‎)×‎‎1‎‎23‎， ‎=1×‎‎1‎‎23‎， ‎=‎‎1‎‎23‎．‎ ‎9.【答案】‎ 在两船出发后的‎40‎分钟至‎80‎分钟时间段内两船可以互相望见。‎ ‎【解答】‎ 解：‎(30-10)÷(60-30)‎ ‎=20÷30‎， ‎=‎‎2‎‎3‎（小时）； ‎2‎‎3‎小时‎=40‎分钟； ‎(30+10)÷(60-30) =40÷30‎， ‎=‎‎4‎‎3‎（小时）； ‎4‎‎3‎小时‎=80‎分钟； 验证：‎60×‎4‎‎3‎=80(km)‎， ‎90+30=120(km)‎， ‎80km<120km， 说明未到达C港，符合题意。 ‎ ‎10.【答案】‎ 两次生意共获利润‎92000‎元。‎ 第21页 共22页 ◎ 第22页 共22页 ‎【解答】‎ 解：第一次进货数量：‎(176000÷2-80000)÷4‎， ‎=8000÷4‎， ‎=2000‎（件）， 第二次进货数量：‎2000×2=4000‎（件） 总利润：‎2000×(58-40)+4000×(58-40-4)‎， ‎=2000×18+4000×14‎， ‎=36000+56000‎， ‎=92000‎（元）； ‎ ‎11.【答案】‎ 他能获得八折优惠价购买粽子的可能性是‎1‎‎6‎．‎ ‎【解答】‎ 解：（1）可能出现的所有结果： 解法一：； 解法二：AC    AD    BC    BD    CC    CD； ‎(2‎ ‎)‎只有在两个转盘都指到C时才符合要求，出现的可能性为：‎1÷6=‎‎1‎‎6‎． 答：他能获得八折优惠价购买粽子的可能性是‎1‎‎6‎．‎ ‎12.【答案】‎ 阴影部分的面积是‎56‎平方厘米。‎ ‎【解答】‎ 解：‎[10+16-(16-10)×2]×8÷2‎， ‎=14×8÷2‎， ‎=14×4‎， ‎=56‎（平方厘米）； ‎ ‎13.【答案】‎ 解：‎11‎‎12‎‎+[1-(‎1‎‎6‎+‎3‎‎8‎)]×‎‎1‎‎4‎， ‎=‎11‎‎12‎+(1-‎13‎‎24‎)×‎‎1‎‎4‎， ‎=‎11‎‎12‎+‎11‎‎24‎×‎‎1‎‎4‎， ‎=‎11‎‎12‎+‎‎11‎‎96‎， ‎=‎‎33‎‎32‎．‎ ‎【解答】‎ 解：‎11‎‎12‎‎+[1-(‎1‎‎6‎+‎3‎‎8‎)]×‎‎1‎‎4‎， ‎=‎11‎‎12‎+(1-‎13‎‎24‎)×‎‎1‎‎4‎， ‎=‎11‎‎12‎+‎11‎‎24‎×‎‎1‎‎4‎， ‎=‎11‎‎12‎+‎‎11‎‎96‎， ‎=‎‎33‎‎32‎．‎ ‎14.【答案】‎ 它的底面积是‎113.04‎厘米。‎ ‎【解答】‎ 解：侧面积‎=‎底面周长‎×‎高‎=‎半径‎×2×3.14×‎高； 体积‎=‎底面积‎×‎高‎=‎半径‎×‎半径‎×3.14×‎高； 半径‎=‎体积‎÷‎侧面积‎×2=942÷314×2=6‎（厘米）； 圆柱底面积是‎6‎‎2‎‎×3.14‎ ‎=36×3.14 =113.04‎（平方厘米）， ‎ ‎15.【答案】‎ 解：‎8‎‎17‎‎÷23+‎1‎‎23‎×‎‎9‎‎17‎ ‎‎=‎8‎‎17‎×‎1‎‎23‎+‎1‎‎23‎×‎9‎‎17‎ ‎‎=(‎8‎‎17‎+‎9‎‎17‎)×‎1‎‎23‎ ‎‎=1×‎1‎‎23‎ ‎‎=‎‎1‎‎23‎ ‎【解答】‎ 解：‎8‎‎17‎‎÷23+‎1‎‎23‎×‎‎9‎‎17‎ ‎‎=‎8‎‎17‎×‎1‎‎23‎+‎1‎‎23‎×‎9‎‎17‎ ‎‎=(‎8‎‎17‎+‎9‎‎17‎)×‎1‎‎23‎ ‎‎=1×‎1‎‎23‎ ‎‎=‎‎1‎‎23‎ ‎16.【答案】‎ 当列车完全超过乙车时，列车离开A站‎45.3‎千米。 或用下列解法： 解：‎9‎秒‎=‎‎1‎‎400‎小时，‎12‎秒‎=‎‎1‎‎300‎小时 假如两辆车的长度忽略不计，设列车的速度为x千米/时，得： ‎(x-30)×‎1‎‎400‎=(x-45)×‎1‎‎300‎ ‎          x=90‎ ‎ 第21页 共22页 ◎ 第22页 共22页 列车的长度为：‎(90-30)×‎1‎‎400‎=‎‎3‎‎20‎（千米） 列车从出发到完全超过乙车所需要的时间：‎(45×0.5+‎3‎‎20‎)÷(90-45)=‎‎453‎‎900‎； 当列车完全超过乙车时，列车离开A站的距离为：‎90×‎453‎‎900‎=45.3‎（千米）； 答：当列车完全超过乙车时，列车离开A站‎45.3‎千米。‎ ‎【解答】‎ 解：设列车的速度为s，由题意可得： ‎(s-30)×9=(s-45)×12‎，     ‎9s-270=12s-540‎，     ‎12s-9s=540-270‎，         ‎3s=270‎，          s=90‎； 设火车到达乙车的时间为t，由题意可得：  ‎90×t=45(t+0.5)‎，    ‎90t=45t+22.5‎， ‎90t-45t=22.5‎，    ‎45t=22.5‎，      t=0.5‎； ‎90×(‎1‎‎2‎+‎12‎‎3600‎)‎， ‎=90×‎‎151‎‎300‎， ‎=45.3‎（千米）； ‎ ‎17.【答案】‎ 做了‎84‎张桌子，‎50‎把椅子。‎ ‎【解答】‎ 解：假设‎20‎天全做桌子， ‎20×(2+3)=100‎（张）， ‎134-100=34‎（张）， ‎9-3=6‎（把）， ‎7-2=5‎（把）， ‎34=24+10=4×6+2×5‎， 所以甲多做了‎4‎天，乙多做了‎2‎天， ‎4×9+2×7=50‎（把）， ‎134-50=84‎（张）， ‎ ‎18.【答案】‎ 原来长方形的面积是‎36‎平方厘米。‎ ‎【解答】‎ 解：设这个长方形的长是x厘米，则宽为x-5‎厘米； x(x-5)=(x-3)(x-3)‎，   x‎2‎‎-5x=x‎2‎-6x+9‎，       x=9‎， x-5=9-5=4‎； ‎9×4=36‎（平方厘米）； ‎ ‎19.【答案】‎ 这个商人赔了，赔了‎10‎元。‎ ‎【解答】‎ 解：赔的钱数： ‎120÷(1-20%)-120‎， ‎=120÷0.8-120‎， ‎=150-120‎， ‎=30‎（元）； 赚的钱数： ‎120-120÷(1+20%)‎， ‎=120-120÷1.2‎， ‎=120-100‎， ‎=20‎（元）． 因为‎30‎元‎>20‎元，所以商人赔了， ‎30-20=10‎（元）． ‎ ‎20.【答案】‎ 解：‎20÷[63×(‎5‎‎7‎-‎5‎‎9‎)×‎2‎‎5‎]‎， ‎=20÷[(63×‎5‎‎7‎-63×‎5‎‎9‎)×‎2‎‎5‎]‎， ‎=20÷[(45-35)×‎2‎‎5‎]‎， ‎=20÷[10×‎2‎‎5‎]‎， ‎=20÷4‎， ‎=5‎．‎ ‎【解答】‎ 解：‎20÷[63×(‎5‎‎7‎-‎5‎‎9‎)×‎2‎‎5‎]‎， ‎=20÷[(63×‎5‎‎7‎-63×‎5‎‎9‎)×‎2‎‎5‎]‎， ‎=20÷[(45-35)×‎2‎‎5‎]‎， ‎=20÷[10×‎2‎‎5‎]‎， ‎=20÷4‎， ‎=5‎．‎ ‎21.【答案】‎ 甲乙两车每秒各行‎20‎米/秒，‎15‎（米/秒）．‎ ‎【解答】‎ 解：甲乙的速度和为：‎350÷10=35‎（米/秒）， 甲乙的速度差为：‎350÷(10+60)=5‎（米/秒）， 甲的速度为：‎(35+5)÷2=20‎（米/秒）， 乙的速度为：‎(35-5)÷2=15‎（米/秒）， ‎ ‎22.【答案】‎ 三角形AEF的面积是‎540‎平方厘米。‎ ‎【解答】‎ 第21页 共22页 ◎ 第22页 共22页 解：线段CE的长度：‎18×5-40×2=10‎（厘米）， 线段DE的长度：‎40-10=30‎（厘米）， 线段AF的长度：‎18×2=36‎（厘米）， 因为四边形ABCD是正方形。 所以DE是三角形AEF的高。 所以三角形AEF的面积：S=AF×DE÷2‎， ‎=36×30÷2‎， ‎=540‎（平方厘米）， ‎ ‎23.【答案】‎ 妈妈的卖法挣钱多。‎ ‎【解答】‎ 解：妈妈的卖法，收入： ‎30÷3+30÷2‎， ‎=10+15‎， ‎=25‎（元）． 小莉的卖法，收入： ‎(30+30)÷5×2‎， ‎=60÷5×2‎， ‎=24‎（元） ‎ ‎24.【答案】‎ 李明家上月消费‎48.6‎元。‎ ‎【解答】‎ 解：‎(25-22)×3+22×1.8‎， ‎=3×3+39.6‎， ‎=9+39.6‎， ‎=48.6‎（元）． ‎ ‎25.【答案】‎ 圆柱的高应是‎4‎厘米 ‎【解答】‎ ‎(7×6×4.5+5×5×5)÷78.5‎‎， ＝‎314÷78.5‎， ＝‎4‎（厘米）；‎ ‎26.【答案】‎ 这个长方体的体积是‎12.56‎立方分米 ‎【解答】‎ 一个侧面面积＝比原来圆柱的表面积增加的面积‎÷2‎ ＝‎8÷2‎ ＝‎4‎（平方分米）； 底面周长的一半＝πd÷2‎ ＝‎3.14×2÷2‎ ＝‎3.14‎（分米）； V＝一个侧面面积‎×‎底面周长的一半 ＝‎4×3.14‎ ＝‎12.56‎（立方分米）；‎ ‎27.【答案】‎ 体育场买蓝球付‎400‎元，买足球付‎360‎元 ‎【解答】‎ 设足球的价格为x，则蓝球的价格为‎5‎‎6‎x，由此可知方程： ‎12x+16×‎5‎‎6‎x＝‎760‎ ‎76‎‎3‎x＝‎760‎， x＝‎30‎； 所以，买蓝球付：‎30×‎5‎‎6‎×16‎＝‎400‎（元）； 买足球付：‎30×12‎＝‎360‎（元）．‎ ‎28.【答案】‎ 精简了‎37.5%‎ ‎【解答】‎ ‎45‎‎75+45‎‎×100% =‎45‎‎120‎×100%‎‎， ＝‎0.375×100%‎， ＝‎37.5%‎；‎ 三、 应用题 （本题共计 12 小题 ，每题 15 分 ，共计180分 ） ‎ ‎29.【答案】‎ 解：‎10÷45=‎‎2‎‎9‎（小时）； ‎(‎2‎‎9‎×10)÷(35+45)‎， ‎=‎20‎‎9‎÷80‎， ‎=‎‎1‎‎36‎（小时）； ‎1‎‎36‎‎+‎2‎‎9‎=‎‎1‎‎4‎（小时）． 答：‎1‎号队员从离队开始到与队员重新会合，经历了‎1‎‎4‎小时。‎ ‎【解答】‎ 解：‎10÷45=‎‎2‎‎9‎（小时）； ‎(‎2‎‎9‎×10)÷(35+45)‎， ‎=‎20‎‎9‎÷80‎， ‎=‎‎1‎‎36‎（小时）； ‎1‎‎36‎‎+‎2‎‎9‎=‎‎1‎‎4‎（小时）． 答：‎1‎号队员从离队开始到与队员重新会合，经历了‎1‎‎4‎小时。‎ ‎30.【答案】‎ ‎625×(1-20%)×(1+8%)‎‎， ＝‎625×80%×108%‎， ＝‎500×108%‎， ‎ 第21页 共22页 ◎ 第22页 共22页 ‎＝‎540‎（元）； ‎(540-500)÷500‎， ＝‎40÷500‎， ＝‎8%‎； 答：在‎5‎月份销售该商品预计可达到的利润率为‎8%‎ ‎【解答】‎ ‎625×(1-20%)×(1+8%)‎‎， ＝‎625×80%×108%‎， ＝‎500×108%‎， ＝‎540‎（元）； ‎(540-500)÷500‎， ＝‎40÷500‎， ＝‎8%‎； 答：在‎5‎月份销售该商品预计可达到的利润率为‎8%‎ ‎31.【答案】‎ 设甲先干了‎(14-x)‎天，乙干了x天。 ‎1‎‎20‎‎(14-x)+‎1‎‎12‎x＝‎1‎， ‎42‎‎60‎‎-‎3‎‎60‎x+‎5x‎60‎=1‎， ‎2x‎60‎‎+‎42‎‎60‎=1‎， ‎1‎‎30‎x+‎42‎‎60‎-‎42‎‎60‎=1-‎‎42‎‎60‎， ‎1‎‎30‎x×30=‎18‎‎60‎×30‎， x＝‎9‎； ‎14-x＝‎14-9‎＝‎5‎（天）； 答；这样工作由甲先做了‎5‎天。‎ ‎【解答】‎ 设甲先干了‎(14-x)‎天，乙干了x天。 ‎1‎‎20‎‎(14-x)+‎1‎‎12‎x＝‎1‎， ‎42‎‎60‎‎-‎3‎‎60‎x+‎5x‎60‎=1‎， ‎2x‎60‎‎+‎42‎‎60‎=1‎， ‎1‎‎30‎x+‎42‎‎60‎-‎42‎‎60‎=1-‎‎42‎‎60‎， ‎1‎‎30‎x×30=‎18‎‎60‎×30‎， x＝‎9‎； ‎14-x＝‎14-9‎＝‎5‎（天）； 答；这样工作由甲先做了‎5‎天。‎ ‎32.【答案】‎ 麦堆的体积： ‎1‎‎3‎‎×3.14×‎2‎‎2‎×3‎， ＝‎3.14×4‎， ＝‎12.56‎（立方米）， 小麦的重量： ‎12.56×750‎＝‎9420‎（千克）； 答：这堆小麦重‎9420‎千克 ‎【解答】‎ 麦堆的体积： ‎1‎‎3‎‎×3.14×‎2‎‎2‎×3‎， ＝‎3.14×4‎， ＝‎12.56‎（立方米）， 小麦的重量： ‎12.56×750‎＝‎9420‎（千克）； 答：这堆小麦重‎9420‎千克 ‎33.【答案】‎ 两车的速度和为： ‎90÷‎2‎‎3‎=135‎（千米/小时）． 则甲车的速度为： ‎135×‎4‎‎5+4‎ ‎＝‎135×‎‎4‎‎9‎， ＝‎60‎（千米/小时）． 乙车的速度为： ‎135-60‎＝‎75‎（千米/小时）． 答：甲车每小时行‎60‎千米，乙车每小时行‎75‎千米 ‎【解答】‎ 两车的速度和为： ‎90÷‎2‎‎3‎=135‎（千米/小时）． 则甲车的速度为： ‎135×‎4‎‎5+4‎ ‎＝‎135×‎‎4‎‎9‎， ＝‎60‎（千米/小时）． 乙车的速度为： ‎135-60‎＝‎75‎（千米/小时）． 答：甲车每小时行‎60‎千米，乙车每小时行‎75‎千米 ‎34.【答案】‎ ‎30×(20%+10%)‎‎， ＝‎30×‎‎3‎‎10‎， ＝‎9‎（天）； 答：这个地区四月份的雨天有‎9‎天。‎ ‎1-20%-10%-(20%+10%)‎‎， ＝‎1-60%‎， ＝‎40%‎； ‎30×40%‎＝‎12‎（天）； 答：晴天的天数占这个月总天数的‎40%‎，是‎12‎天。‎ ‎【解答】‎ ‎30×(20%+10%)‎‎， ＝‎30×‎‎3‎‎10‎， ＝‎9‎（天）； ‎ 第21页 共22页 ◎ 第22页 共22页 答：这个地区四月份的雨天有‎9‎天。‎ ‎1-20%-10%-(20%+10%)‎‎， ＝‎1-60%‎， ＝‎40%‎； ‎30×40%‎＝‎12‎（天）； 答：晴天的天数占这个月总天数的‎40%‎，是‎12‎天。‎ ‎35.【答案】‎ 鞋子的购进价是：‎120÷15%‎＝‎800‎（元）， ‎80‎双鞋子的售价是：‎800-64‎＝‎736‎（元）， 每双鞋子的售价是：‎736÷80‎＝‎9.2‎（元）， 每双鞋子的购进价是：‎9.2÷(1+15%)‎＝‎8‎（元）． 答：鞋子的购进价每双‎8‎元 ‎【解答】‎ 鞋子的购进价是：‎120÷15%‎＝‎800‎（元）， ‎80‎双鞋子的售价是：‎800-64‎＝‎736‎（元）， 每双鞋子的售价是：‎736÷80‎＝‎9.2‎（元）， 每双鞋子的购进价是：‎9.2÷(1+15%)‎＝‎8‎（元）． 答：鞋子的购进价每双‎8‎元 ‎36.【答案】‎ 解：‎1‎‎5‎‎-‎1‎‎9‎=‎‎4‎‎45‎， ‎2÷(‎1‎‎9‎-‎4‎‎45‎)‎， ‎=2÷‎‎1‎‎45‎， ‎=90‎（个）； 答：这批零件共有‎90‎个。‎ ‎【解答】‎ 解：‎1‎‎5‎‎-‎1‎‎9‎=‎‎4‎‎45‎， ‎2÷(‎1‎‎9‎-‎4‎‎45‎)‎， ‎=2÷‎‎1‎‎45‎， ‎=90‎（个）； 答：这批零件共有‎90‎个。‎ ‎37.【答案】‎ ‎(150+30)×25 ‎‎＝‎180×25‎ ＝‎4500‎（吨） ‎4500÷150‎＝‎30‎（天）． 答：原计划完成生产任务需要‎30‎天 ‎【解答】‎ ‎(150+30)×25 ‎‎＝‎180×25‎ ＝‎4500‎（吨） ‎4500÷150‎＝‎30‎（天）． 答：原计划完成生产任务需要‎30‎天 ‎38.【答案】‎ ‎3.14×1.2×120×1.5‎‎， ＝‎3.768×120×1.5‎， ＝‎452.16×1.5‎， ＝‎678.24‎（平方米）； 答：被压路面的面积是‎678.24‎平方米 ‎【解答】‎ ‎3.14×1.2×120×1.5‎‎， ＝‎3.768×120×1.5‎， ＝‎452.16×1.5‎， ＝‎678.24‎（平方米）； 答：被压路面的面积是‎678.24‎平方米 ‎39.【答案】‎ ‎180÷4‎‎＝‎45‎（千米） ‎405-180‎＝‎225‎（千米） ‎225÷45‎＝‎5‎（小时） 答：再行驶‎5‎小时，这辆汽车就可以到达乙地 ‎【解答】‎ ‎180÷4‎‎＝‎45‎（千米） ‎405-180‎＝‎225‎（千米） ‎225÷45‎＝‎5‎（小时） 答：再行驶‎5‎小时，这辆汽车就可以到达乙地 ‎40.【答案】‎ 解：甲乙合做，需要的天数： ‎1÷(‎1‎‎12‎+‎1‎‎18‎)‎， ‎=1÷‎‎5‎‎36‎， ‎=1×‎‎36‎‎5‎， ‎=7.2‎（小时）； 各干‎7‎小时后，还剩： ‎1-(‎1‎‎12‎+‎1‎‎18‎)×7‎， ‎=1-‎5‎‎36‎×7‎， ‎=1-‎‎35‎‎36‎， ‎=‎‎1‎‎36‎； 甲来完成这‎1‎‎36‎，用的时间： ‎1‎‎36‎‎÷‎‎1‎‎12‎， ‎=‎1‎‎36‎×12‎， ‎=‎‎1‎‎3‎（小时）； 所以总共用： ‎7×2+‎1‎‎3‎=14‎‎1‎‎3‎（小时）； 答：完成任务时共用了‎14‎‎1‎‎3‎小时。‎ ‎【解答】‎ 解：甲乙合做，需要的天数： ‎ 第21页 共22页 ◎ 第22页 共22页 ‎1÷(‎1‎‎12‎+‎1‎‎18‎)‎‎， ‎=1÷‎‎5‎‎36‎， ‎=1×‎‎36‎‎5‎， ‎=7.2‎（小时）； 各干‎7‎小时后，还剩： ‎1-(‎1‎‎12‎+‎1‎‎18‎)×7‎， ‎=1-‎5‎‎36‎×7‎， ‎=1-‎‎35‎‎36‎， ‎=‎‎1‎‎36‎； 甲来完成这‎1‎‎36‎，用的时间： ‎1‎‎36‎‎÷‎‎1‎‎12‎， ‎=‎1‎‎36‎×12‎， ‎=‎‎1‎‎3‎（小时）； 所以总共用： ‎7×2+‎1‎‎3‎=14‎‎1‎‎3‎（小时）； 答：完成任务时共用了‎14‎‎1‎‎3‎小时。‎ 第21页 共22页 ◎ 第22页 共22页