6年级数学教案第7讲：有理数的运算（一） 8页

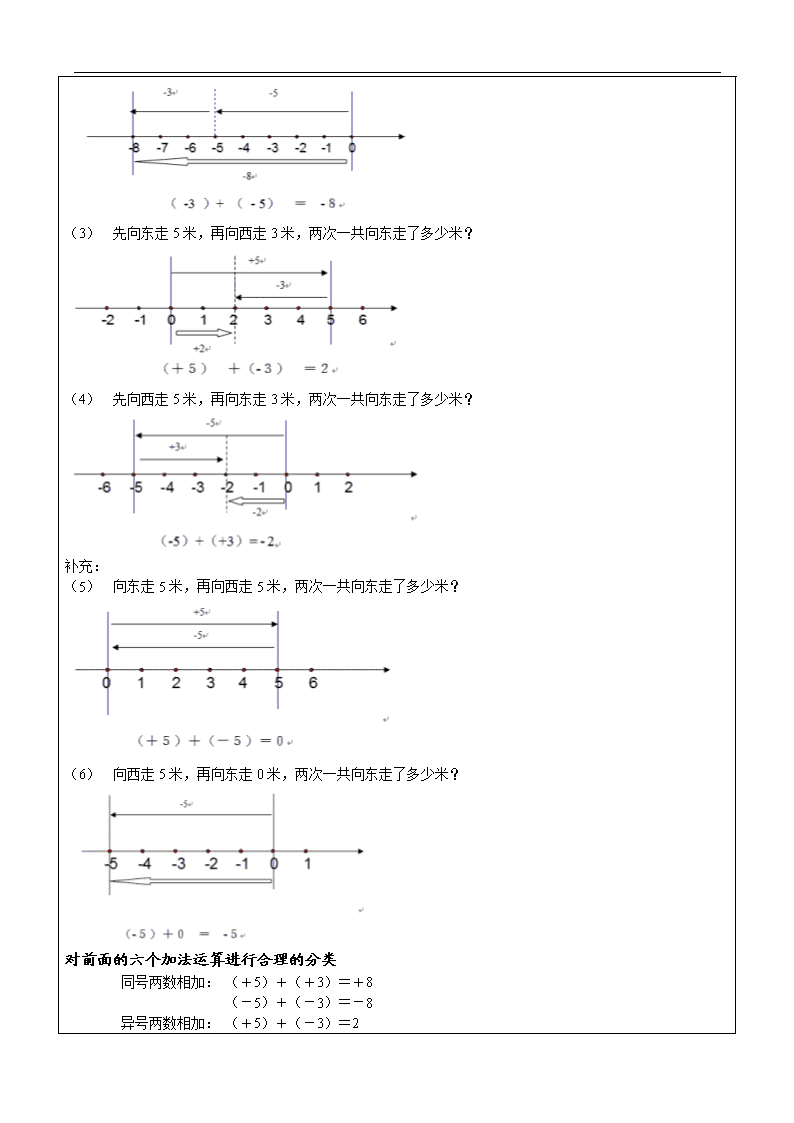
辅导教案 学员姓名： 学科教师：‎ 年 级： 辅导科目：‎ 授课日期 ‎××年××月××日 时 间 A / B / C / D / E / F段 主 题 有理数的运算（一）‎ 教学内容 1． 掌握有理数加法法则，并能准确地进行有理数加法运算，能灵活运用加法运算律简化加法运算；‎ 2． 掌握有理数减法法则，并熟练的进行有理数减法运算。‎ ‎（此环节设计时间在40-50分钟）‎ 教法说明：新授课内容，学科教师根据案例引导学生对知识点进行学习。‎ 案例1：小明在一条东西向的跑道上，先走了‎5米，又走了‎3米，能否确定他现在位于原来位置的哪个方向？相距多少米？（规定向东的方向为正方向）‎ 思考讨论，小明走动路线有几种情况 有以下四种走动的情况：‎ ‎（1）两次都向东走； （2）两次都向西走；‎ ‎（3）先向东走，再向西走； （4）先向西走，再向东走。‎ 分析每一种情况，并在数轴上表示出来 （1） 向东走‎5米，再向东走‎3米，一共向东走了多少米？‎ （2） 向西走- ‎5米，再向西走- ‎3米，一共向东走了多少米？‎ （1） 先向东走‎5米，再向西走‎3米，两次一共向东走了多少米？‎ （2） 先向西走‎5米，再向东走‎3米，两次一共向东走了多少米？‎ 补充：‎ （3） 向东走5米，再向西走5米，两次一共向东走了多少米？‎ （4） 向西走5米，再向东走‎0米，两次一共向东走了多少米？‎ 对前面的六个加法运算进行合理的分类 ‎ 同号两数相加： （＋5）＋（＋3）＝＋8‎ ‎ （－5）＋（－3）＝－8‎ ‎ 异号两数相加： （＋5）＋（－3）＝2‎ ‎ 　　　 （－5）＋（＋3）＝－2‎ ‎ 　 （＋5）＋（－5）＝0‎ ‎ 一数与零相加： （－5）+ 0 = －5‎ 归纳总结：‎ 教法说明：让学生自己来总结有理数的加法法则，以下可以设置为填空。‎ 有理数加法法则 同号两数相加：取原来的符号，并把绝对值相加。‎ 异号两数相加：绝对值相等时和为零；绝对值不相等时，其和的绝对值为较大的绝对值减去较小的绝对值所得的差，其和的符号取绝对值较大的加数的符号。‎ 一个数同零相加：仍得这个数。‎ 根据有理数的加法法则完成以下四题：‎ 计算：‎ ‎（1） （2）‎ ‎（3） （4）‎ 答案：（1）﹣200； （2）﹣2； （3）； （4）‎ 复习有理数的加法运算律：‎ 教法说明：要求让学生自己回忆分数加法运算中学过的加法运算律。‎ 有理数加法运算律 交换律：‎ 结合律：‎ ‎（1）计算：‎ 教法指导：学科教师可以通过提问的方式让学生回答常见的分数化小数以及小数化分数，如：化为分数是多少，化为小数是多少，等等。‎ ‎（2）计算：‎ 教法指导：通过学生之间的相互讨论，归纳和总结本题的简便运算。‎ 总结技巧：‎ 对于三个以上有理数相加，按下列过程计算比较简便：‎ ‎1．其中的相反数相加；‎ ‎2．再将正数、负数分别相加；‎ ‎3．最后求出异号加数的和。遇到小数、分数时，可把相加得整数的先加起来。‎ 有理数减法法则 减去一个数，等于加上这个数的相反数：‎ 计算：‎ ‎（1） （2）‎ 教法说明：重点引导学生对有理数的减法法则的理解，通过减法转化为加法来进行计算。‎ 解：原式 解：原式 ‎（此环节设计时间在20-30分钟）‎ 例题1：计算 ‎ 教法指导：要让学生自己观察题目中的数字之间的关系，怎样组合计算更简单，学科教师要适当提醒（本题需要关注小数化分数，同分母的分数）‎ 试一试：计算 ‎ 例题2：计算 ‎ 教法指导：学科教师重点要引导学生将减法运算转化为加法运算，重点强调 试一试：计算 ‎ 此环节设计时间在30分钟左右（20分钟练习+10分钟互动讲解）。‎ 1． 计算：‎ 教法说明：本题要求学生用简便方法进行计算，把正数与负数分别结合相加比较简便。‎ 2． 计算：‎ 教法说明：把同分母的分数、互为相反数的数分别结合相加比较方便。‎ 3． 计算：‎ 教法说明：先运用有理数减法法则，变减法为加法，再由有理数加法法则进行计算。‎ 解：原式（统一成加法）‎ ‎ （加法交换律）‎ ‎ ‎ ‎ （加法结合律） ‎ ‎ ‎ 4． 计算：‎ 解：原式 （写成和的形式）‎ ‎ （加法结合律）‎ ‎ ‎ 补充类试题:‎ 计算（要求使用简便方法计算）‎ ‎1． 2．‎ ‎3． 4．‎ 答案：1、﹣9.8； 2、4.25； 3、； 4、12‎ ‎（此环节设计时间在5-10分钟内）‎ 让学生回顾本节课所学的重点知识，以学生自我总结为主，学科教师引导为辅，为本次课做一个总结回顾 有理数的加法法则：‎ 有理数的加法交换律：‎ 有理数的减法法则：‎ 计算（可用简便方法计算）‎ ‎1． 2．‎ ‎3． 4．‎ 答案：1、； 2、； 3、； 4、‎ 预习思考：思考之间的关系？能否写成：‎ 尝试计算以下四题并总结两数相乘结果的符号问题：‎ ‎(1)2×1＝ ； (2)(﹣2)×1＝ ； (3)2×(﹣1)＝ ； (4)(﹣2)×(﹣1)＝ ．‎