2008年陕西省中考数学考试 11页

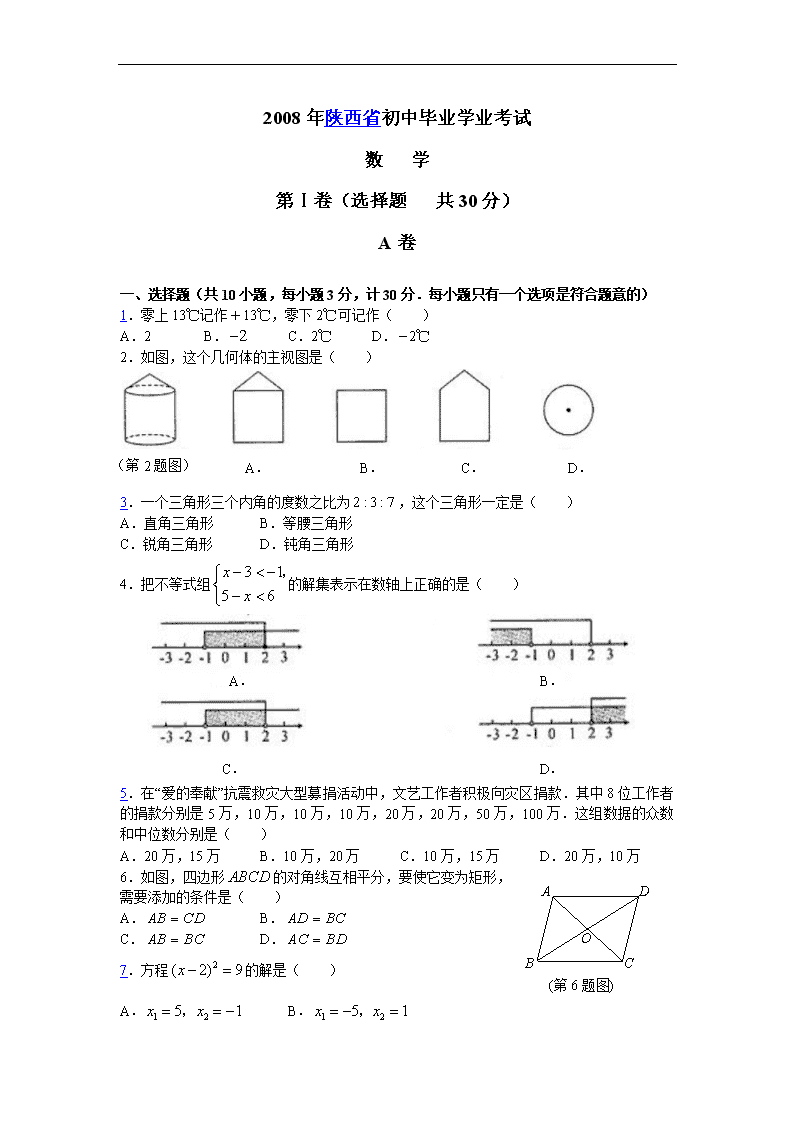
‎2008年陕西省初中毕业学业考试 数 学 第Ⅰ卷（选择题 共30分）‎ A卷 一、选择题（共10小题，每小题3分，计30分．每小题只有一个选项是符合题意的）‎ 1．零上‎13℃‎记作‎13℃‎，零下‎2℃‎可记作（ ）‎ A．2 B． C．2℃ D．2℃‎ ‎2．如图，这个几何体的主视图是（ ）‎ ‎（第2题图）‎ A． B． C． D．‎ 3．一个三角形三个内角的度数之比为，这个三角形一定是（ ）‎ A．直角三角形 B．等腰三角形 C．锐角三角形 D．钝角三角形 ‎ A． B．‎ C． D．‎ ‎4．把不等式组的解集表示在数轴上正确的是（ ）‎ 5．在“爱的奉献”抗震救灾大型募捐活动中，文艺工作者积极向灾区捐款．其中8位工作者的捐款分别是5万，10万，10万，10万，20万，20万，50万，100万．这组数据的众数和中位数分别是（ ）‎ A．20万，15万 B．10万，20万 C．10万，15万 D．20万，10万 ‎(第6题图)‎ O A D C B ‎6．如图，四边形的对角线互相平分，要使它变为矩形，‎ 需要添加的条件是（ ）‎ A． B．‎ C． D．‎ 7．方程的解是（ ）‎ A． B．‎ ‎(第8题图)‎ ‎3‎ y x B A ‎2‎ C． D．‎ ‎8．如图，直线对应的函数表达式是（ ）‎ A． B． ‎ C． D．‎ 9．如图，直线与半径为2的相切于点是上 O ‎(第9题图)‎ D F E A C B 一点，且，弦，则的长度为（ ）‎ A．2 B． C． D．‎ ‎10．已知二次函数（其中），‎ 关于这个二次函数的图象有如下说法：‎ ‎①图象的开口一定向上；‎ ‎②图象的顶点一定在第四象限；‎ ‎③图象与轴的交点至少有一个在轴的右侧．‎ 以上说法正确的个数为（ ）‎ A．0 B．1 C．2 D．3‎ B卷 第Ⅱ卷（非选择题 共90分）‎ 二、填空题（共6小题，每小题3分，计18分）‎ 11．若，则的余角的大小是 ．‎ ‎12．计算： ．‎ ‎(第14题图)‎ O ‎(B)‎ A D x y C 13．一个反比例函数的图象经过点，则这个函数的表达 式是 ．‎ ‎14．如图，菱形的边长为2，，‎ 则点的坐标为 ．‎ 15．搭建如图①的单顶帐篷需要17根钢管，这样的帐篷按图②，‎ 图③的方式串起来搭建，则串7顶这样的帐篷需要 根钢管．‎ 图1 图2 图3‎ ‎(第15题图)‎ A B D C ‎(第16题图)‎ ‎16．如图，梯形中，，‎ ‎，且，分别以 为边向梯形外作正方形，其面积分别为，则之间的关系 是 ．‎ 三、解答题（共9小题，计72分．解答应写出过程）‎ 17．（本题满分6分）‎ 先化简，再求值：‎ ‎，其中，．‎ ‎18．（本题满分6分）‎ 已知：如图，三点在同一条直线上，，，．‎ A D B C E ‎(第18题图)‎ 求证：．‎ 19．（本题满分7分）‎ 下面图①，图②是某校调查部分学生是否知道母亲生日情况的扇形和条形统计图：‎ 不知道 记不清 图①‎ 学生数/名 ‎50‎ ‎40‎ ‎30‎ ‎20‎ ‎10‎ 选项 知道 记不清 不知道 图②‎ ‎(第19题图)‎ 知道 根据上图信息，解答下列问题：‎ ‎（1）求本次被调查学生的人数，并补全条形统计图；‎ ‎（2）若全校共有2700名学生，你估计这所学校有多少名学生知道母亲的生日？‎ ‎（3）通过对以上数据的分析，你有何感想？（用一句话回答）‎ ‎20．（本题满分7分）‎ 阳光明媚的一天，数学兴趣小组的同学们去测量一棵树的高度（这棵树底部可以到达，顶部不易到达），他们带了以下测量工具：皮尺、标杆、一副三角尺、小平面镜．请你在他们提供的测量工具中选出所需工具，设计一种测量方案．‎ ‎（1）所需的测量工具是： ；‎ ‎（2）请在下图中画出测量示意图；‎ ‎（3）设树高的长度为，请用所测数据（用小写字母表示）求出．‎ 第20题图 21．（本题满分8分）‎ 如图，桌面上放置了红、黄、蓝三个不同颜色的杯子，杯口朝上．我们做蒙眼睛翻杯子（杯口朝上的翻为杯口朝下，杯口朝下的翻为杯口朝上）的游戏．‎ ‎（1）随机翻一个杯子，求翻到黄色杯子的概率；‎ ‎（2）随机翻一个杯子，接着从这三个杯子中再随机翻一个，请利用树状图求出此时恰好有一个杯口朝上的概率．‎ 红 黄 蓝 ‎(第21题图)‎ ‎22．（本题满分8分）‎ 项目 生态公园计划在园内的坡地上造一片有两种树的混合体，需要购买这两种树苗2000棵．种植两种树苗的相关信息如下表：‎ 品种 单价（元/棵）‎ 成活率 劳务费（元/棵）‎ A ‎15‎ ‎3‎ B ‎20‎ ‎4‎ 设购买种树苗棵，造这片林的总费用为元．解答下列问题：‎ ‎（1）写出（元）与（棵）之间的函数关系式；‎ ‎（2）假设这批树苗种植后成活1960棵，则造这片林的总费用需多少元？‎ 23．（本题满分8分）‎ 如图，在中，，，，是的角平分线．过三点的圆与斜边交于点，连接．‎ A C D E B ‎(第23题图)‎ ‎（1）求证：；‎ ‎（2）求外接圆的半径．‎ ‎24．（本题满分10分）‎ 如图，矩形的长、宽分别为和1，且，点，连接．‎ ‎（1）求经过三点的抛物线的表达式；‎ ‎（2）若以原点为位似中心，将五边形放大，使放大后的五边形的边长是原五边形对应边长的3倍．请在下图网格中画出放大后的五边形；‎ ‎1‎ O x y ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎7‎ ‎6‎ ‎5‎ ‎4‎ ‎3‎ ‎2‎ ‎1‎ A B C D E ‎（第24题图）‎ ‎（3）经过三点的抛物线能否由（1）中的抛物线平移得到？请说明理由．‎ 25．（本题满分12分）‎ 某县社会主义新农村建设办公室，为了解决该县甲、乙两村和一所中学长期存在的饮水困难问题，想在这三个地方的其中一处建一所供水站．由供水站直接铺设管道到另外两处．‎ 如图，甲，乙两村坐落在夹角为的两条公路的段和段（村子和公路的宽均不计），点表示这所中学．点在点的北偏西的‎3km处，点在点的正西方向，点在点的南偏西的km处．‎ 为使供水站铺设到另两处的管道长度之和最短，现有如下三种方案：‎ 方案一：供水站建在点处，请你求出铺设到甲村某处和乙村某处的管道长度之和的最小值；‎ 方案二：供水站建在乙村（线段某处），甲村要求管道建设到处，请你在图①中，画出铺设到点和点处的管道长度之和最小的线路图，并求其最小值；‎ 方案三：供水站建在甲村（线段某处），请你在图②中，画出铺设到乙村某处和点处的管道长度之和最小的线路图，并求其最小值．‎ 综上，你认为把供水站建在何处，所需铺设的管道最短？‎ M A E C D B F 乙村 甲村 东 北 图①‎ M A E C D B F 乙村 甲村 图②‎ ‎(第25题图)‎ O O ‎2008年陕西省初中毕业学业考试 数学参考答案（Ａ卷）‎ 一、选择题 1．D　　2．A　　3．D　　4．C　　5．C　　‎ ‎6．D　　7．A　　8．A　　9．B　　10．C 二、填空题 11．　　12．　　13．　　14．‎ ‎15．83　　 16．‎ 三、解答题 17．解：原式 （1分）‎ ‎ （2分）‎ ‎ （3分）‎ ‎ （4分）‎ 当，时，原式 （6分）‎ ‎18．证明：，‎ ‎，． （2分）‎ 又，‎ ‎． （4分）‎ 又，‎ ‎． （6分）‎ 19．解：（1）（名），‎ 本次调查了90名学生． （2分）‎ 补全的条形统计图如下：‎ 学生数／名 ‎50‎ ‎40‎ ‎30‎ ‎20‎ ‎10‎ 选项 知道 记不清 不知道 ‎(第19题答案图)‎ ‎ （4分）‎ ‎（2）（名），‎ 估计这所学校有1500名学生知道母亲的生日． （6分）‎ ‎（3）略（语言表述积极进取，健康向上即可得分）． （7分）‎ ‎20．解：（1）皮尺、标杆． （1分）‎ ‎（2）测量示意图如右图所示． （3分）‎ ‎（3）如图，测得标杆，树和标杆的影长分别为，． （5分）‎ C D E F B A ‎（第20题答案图）‎ ‎，‎ ‎．‎ ‎．‎ ‎． （7分）‎ ‎※注：其它符合题意的正确解答参照以上解题过程赋分．‎ 21．解：（1）（翻到黄色杯子）． （3分）‎ ‎（2）将杯口朝上用“上”表示，杯口朝下用“下”表示，画树状图如下：‎ 开始（上，上，上）‎ ‎（上，上，上）‎ ‎（上，下，下）‎ ‎（下，上，下）‎ ‎（上，上，下）‎ ‎（上，下，下）‎ ‎（上，上，上）‎ ‎（下，下，上）‎ ‎（上，下，上）‎ ‎（下，上，下）‎ ‎（下，下，上）‎ ‎（上，上，上）‎ ‎（下，上，上）‎ ‎（第21题答案图）‎ 由上面树状图可知：所有等可能出现的结果共有9种，其中恰好有一个杯口朝上的有6种，‎ ‎ （7分）‎ ‎（恰好有一个杯口朝上）． （8分）‎ ‎22．解：（1） （3分）‎ ‎（2）由题意，可得：．‎ ‎． （5分）‎ 当时，．‎ 造这片林的总费用需45 000元． （8分）‎ 23．（1）证明：，为直径． （1分）‎ 又是的角平分线，‎ ‎，．‎ ‎． （3分）‎ ‎（2）解：，‎ ‎．‎ ‎，．‎ 为直径，．‎ ‎，． （6分）‎ ‎．．‎ ‎．‎ 外接圆的半径为． （8分）‎ ‎24．解：（1）设经过三点的抛物线的表达式为．‎ ‎． （1分）‎ ‎，解之，得．‎ 过三点的抛物线的表达式为． （4分）‎ ‎（2）‎ ‎（第24题答案图）‎ ‎ （7分）‎ ‎（3）不能．理由如下： （8分）‎ 设经过三点的抛物线的表达式为．‎ ‎，‎ ‎，解之，得．‎ ‎，，．‎ 经过三点的抛物线不能由（1）中抛物线平移得到． （10分）‎ 25．解：方案一：由题意可得：，‎ 点到甲村的最短距离为． （1分）‎ 点到乙村的最短距离为．‎ 将供水站建在点处时，管道沿铁路建设的长度之和最小．‎ 即最小值为． （3分）‎ 方案二：如图①，作点关于射线的对称点，则，连接交于点，则．‎ ‎，． （4分）‎ 在中，‎ ‎，，‎ ‎，两点重合．即过点． （6分）‎ 在线段上任取一点，连接，则．‎ ‎，‎ 把供水站建在乙村的点处，管道沿线路铺设的长度之和最小．‎ M A E C D B F 甲村 东 北 M A E C D B F ‎(第25题答案图①)‎ A G H ‎(第25题答案图②)‎ P O O N 即最小值为． （7分）‎ 方案三：作点关于射线的对称点，连接，则．‎ 作于点，交于点，交于点，‎ 为点到的最短距离，即．‎ 在中，，，‎ ‎．．‎ ‎，两点重合，即过点．‎ 在中，，． （10分）‎ 在线段上任取一点，过作于点，连接．‎ 显然．‎ 把供水站建在甲村的处，管道沿线路铺设的长度之和最小．‎ 即最小值为． （11分）‎ 综上，，供水站建在处，所需铺设的管道长度最短． （12分）‎