中考数学总复习知识点聚焦二次函数 13页

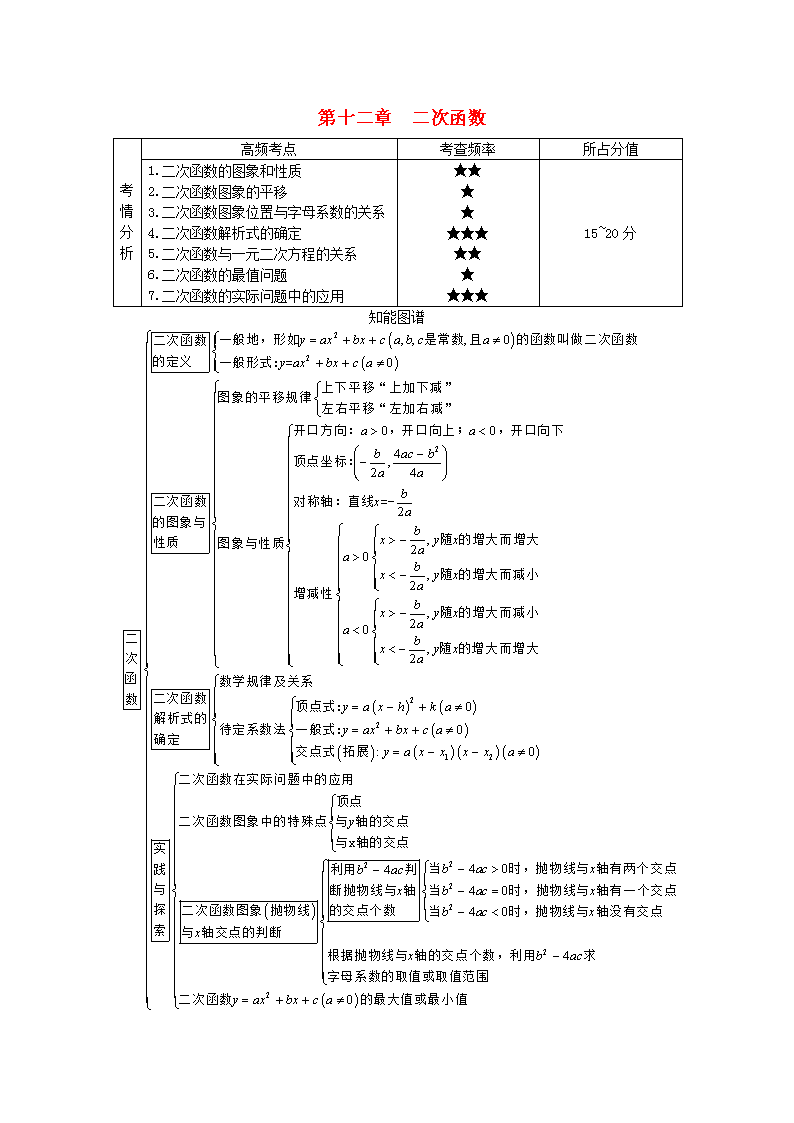
‎ 第十二章 二次函数 考情分析 高频考点 考查频率 所占分值 ‎1.二次函数的图象和性质 ‎2.二次函数图象的平移 ‎3.二次函数图象位置与字母系数的关系 ‎4.二次函数解析式的确定 ‎5.二次函数与一元二次方程的关系 ‎6.二次函数的最值问题 ‎7.二次函数的实际问题中的应用 ‎★★‎ ‎★‎ ‎★‎ ‎★★★‎ ‎★★‎ ‎★‎ ‎★★★‎ ‎15~20分 知能图谱 ‎ 第26讲 二次函数的定义、图象及性质 知识能力解读 知能解读(一)二次函数的定义 一般地，形如(是常数，且)的函数叫作二次函数.其中是自变量，分别是函数解析式的二次项系数、一次项系数和常数项.例如，等都是二次函数.‎ 注意 ‎(1)任何一个二次函数的解析式都可以化成 (是常数，且)的形式，因此，把 (是常数，且)叫作二次函数的一般式.‎ ‎(2)二次函数中，都是变量，是常量，自变量的取值是全体实数，和可以是任意实数，是不为0的实数，所以二次函数还有如下特殊形式:①: (当时)；② (当时)；③ (当时).‎ ‎(3)二次函数的结构特征:等号右边是关于自变量的二次整式.‎ 知能解读(二)二次函数的图象和性质 二次函数的图象是一条抛物线，它的对称轴是轴，顶点是原点.‎ 图象 开口方向 向上 向下 顶点坐标 对称轴 轴 轴 增减性 当时，随的增大而减小；‎ 当时，随的增大而增大 当时，随的增大而增大；‎ 当时，随的增大而减小 最值 当时，‎ 当时，‎ 注意 ‎(1)(供参考)抛物线的开口大小由决定，越大，抛物线的开口越小；越小，抛物线的开口越大.‎ ‎(2)画的图象时，描点法画出的只是整个图象的一部分，是近似的，由于可取一切实数，所以图象应向两方无限延伸.‎ ‎(3)选取自变量的值时，为了计算方便，一般取整数.‎ 知能解读(三)二次函数 的图象和性质 ‎1二次函数的图象和性质 二次函数的图象是一条拋物线，它的对称轴是轴，顶点坐标是.‎ 二次函数的图象和性质 的符号 图象 开口方向 向上 向下 对称轴 轴(直线)‎ 轴(直线)‎ 顶点坐标 增减性 当时，随的增大而减小；‎ 当时，随的增大而增大 当时，随的增大而增大；‎ 当时，随的增大而减小 最值 当时，‎ 当时，‎ ‎2二次函数的图象和性质 二次函数的图象是一条抛物线，它的对称轴是平行于轴或与轴重合的直线，顶点坐标是.‎ 函数 图象 顶点 最低点 最高 对称轴 直线，当时，对称轴在轴的右侧；‎ 当时，对称轴在轴的左侧 开口方向 向上 向下 增减性 当时，随的增大而减小；‎ 当时，随的增大而增大 当时，随的增大而增大；‎ 当时，随的增大而减小 最值 当时，‎ 当时，‎ ‎3二次函数的图象和性质 二次函数的图象是一条抛物线，它的对称轴是直线，顶点坐标为.‎ 函数 图象 开口方向 向上 向下 对称轴 经过点且平行于轴的直线 经过点且平行于轴的直线 顶点坐标 顶点是图象的最低点，坐标是 顶点是图象的最高点，坐标是 增减性 当时，随的增大而减小；‎ 当时，随的增大而增大（简记为“左减右增”）‎ 当时，随的增大而增大；‎ 当时，随的增大而减小（简记为“左增右减”）‎ 最值 当时，‎ 当时，‎ 注意 ‎(1)由可直接看出抛物线的顶点坐标 ‎(2) 决定抛物线的形状、大小，决定抛物线的位置.‎ 具体的平移操作如图所示.‎ 点拨 ‎(1)对于函数的性质，要注意与对比学习，通过图象得出函数的性质.‎ ‎(2)二次函数的图象可由抛物线的图象平移得到，与的符号分别确定左右平移和上下平移的方向，与的绝对值确定平移的距离.抛物线平移规律是“左右平移，左加右减：上下平移.上加下减”‎ 知能解读(四)二次函数的图象与性质 关系式 一般式 顶点式 图象形状 抛物线 开口方向 当时，开口向上；到那个时，开口向下 顶点坐标 对称轴 增减性 对称轴左侧，即或随增大而减小；‎ 对称轴右侧，即或随增大而增大 对称轴左侧，即或随增大而增大；‎ 对称轴右侧，即或随增大而减小 最大值 当时，‎ 当时，‎ 当时，‎ 当时，‎ 知能解读(五)二次函数图象的画法 ‎(1)描点法，其步骤如下:‎ ‎①把二次函数解析式化成的形式；‎ ‎②确定抛物线的开口方向、对称轴和顶点坐标；‎ ‎③在对称轴两侧，以顶点为中心，左右对称描点画图.‎ 注意 若抛物线与轴有交点，最好选取交点描点，特别是作抛物线草图时，应抓住以下五点:①‎ 开口方向；②对称轴；③顶点；④与轴交点；⑤与轴交点.‎ ‎(2)平移法，其步骤如下：‎ ‎①利用配方法把二次函数解析式化成的形式，确定其顶点坐标；‎ ‎②作出的图象；‎ ‎③将的图象平移，使其顶点移到.‎ 知能解读(六)待定系数法求二次函数的解析式 二次函数解析式有三种常见形式：‎ ‎(1)—般式(或三点式)： (为常数，)；‎ ‎(2)顶点式(或配方式)： (为常数，)；‎ ‎(3)交点式(或两根式)： (是常数，拓展点).‎ 注意 ‎(a)任何一个二次函数解析式通过配方都可以化成顶点式，抛物线顶点坐标为.当时，抛物线顶点在轴上；当时，抛物线顶点在轴上；当时，抛物线顶点在原点处.‎ ‎(2)两根式又叫交点式，是抛物线与轴的交点的横坐标，即交点，交点.‎ ‎ (3)确定二次函数解析式时，根据所给的条件；合理地选择恰当的表达式.一般地，已知抛物线上；任意三点时，通常设函数解析式为一般式；当已知顶点坐标时，通常设函数解析式为顶点式；当已知抛物线与轴的两个交点时，通常设函数解析式为交点式.‎ 知能解读(七)二次函数的图象特征与的符号之间的关系 ‎ 项目 字母 字母的符号 图象的特征 开口向上 开口向下 ‎（同号）‎ ‎（异号）‎ 对称轴为轴 对称轴在轴左侧 对称轴在轴右侧 图象过原点 与轴正半轴相交 与轴负半轴相交 注意 ‎(1)由抛物线的开口方向可确定的符号，简记为“上正下负”.(2)由的符号及对称轴的位置可确定的符号.特殊地，对称轴为轴时，；—般情况可简记为“左同右异”，即对称轴在轴左侧，同号，对称轴在轴右侧，异号.(3)当抛物线与轴交于原点时，，否则可简记为“上正下负”，即抛物线与轴交于轴上方，为正；交于轴下方，为负.‎ 方法技巧归纳 方法技巧(一)识别二次函数的方法 判断一个函数是否为二次函数，主要依据有三条：(1)数解析式的右边必须是整式；⑵化筒后的自变量最高次数是2；(3)二次项系数必须不为零.‎ 方法技巧(二)求二次函数图象的顶点坐标和对称轴的方法 ‎(1)公式法：，所以顶点坐标为，对称轴是直线.‎ ‎(2)配方法:运用配方法，将拋物线的关系式化为的形式，得到顶点为，对称轴是直线.‎ ‎(3)对称点法：由于抛物线是轴对称图形，所以连接对称点所得线段的垂直平分线是对称轴，对称轴与抛物线的交点是顶点.‎ 方法技巧(三)二次函数的图象与性质 二次函数的图象与性质主要有二次函数图象的顶点坐标，二次函数的增减性以及函数与坐标轴的交点等问题.‎ 方法技巧(四)根据二次函数图象获取相关信息的方法 ‎(1)由抛物线的开口方向判断的符号，开口向上，；开口向下，.(2)由抛物线对称轴的位置判断的符号，即对称轴为轴，；对称轴在轴左侧，则同号；对称轴在轴右侧，则异号.(3)由抛物线与轴的交点位置判断的符号，当交点在轴的正半轴上时，；当交点为原点时，；当交点在轴的负半轴上时，.‎ 方法技巧(五)用待定系数法求二次函数解析式的技巧 由于二次函数有多种表达形式，所以我们在求二次函数解析式时，首先要根据已知条件的特点，灵活选择合适的表达形式，然后用“待定系数法”求解，可以达到简便、快捷的效果.‎ ‎1一般式 这是最基本的方法，若已知函数图象上的三个点的坐标，可设函数解析式为.‎ ‎2顶点式 若已知抛物线的顶点或对称轴，则设函数解析式为顶点式，顶点的坐标为，对称轴为直线.‎ ‎3交点式 若已知抛物线与轴的两交点坐标或已知抛物线与轴的一交点坐标与对称轴，可通过设交点式来求解.‎ 方法技巧(六)抛物线的平移技巧 抛物线在平移时，的值不变，改变的只是顶点的位置，即只是或的值发生变化，因此解决抛物线平移问题，要把抛物线解析式化为顶点式，并准确求出抛物线的顶点坐标，然后根据“左加右减，上加下减”的平移规律，即可确定平移后的二次函数解析式.‎ 方法技巧(七)解决二次函数综合题的技巧 当问题的条件不确定时，需要对可能的情况分别讨论，这是二次函数中常用的思想方法.‎ 易混易错辨析 易混易错知识 由已知二次函数图象平移得到另一个二次函数图象时，易将平移方向以及的符号混淆.‎ 易混易错(一)对二次函数的定义理解不透，忽视“”这一隐含条件 易混易错(二)忽视隐含条件致错 易混易错(三)平移时混淆中的符号而出错.‎ 中考试题研究 中考命题规律 二次函数的图象和性质是中考考查的重点内容，主要考查二次函数的平移、图象与性质，二次函数图象位置与表达式中字母系数的关系以及二次函数的综合应用.主要以填空题、选择题或解答题的形式出现.用待定系数法求二次函数的解析式是中考的热点之一.‎ 中考试题(一)二次函数图象的平移 中考试题(二)二次函数的性质 中考试题(三)二次函数的图象位置与系数关系 中考试题(四)二次函数的综合应用 中考试题(五)二次函数性质的综合应用 第27讲 二次函数的实践与探索 知识能力解读 知能解读(一)抛物线与直线的交点 直线与抛物线的交点坐标即方程组的解.‎ 当方程组有两个不同解时两函数图象有两个交点；‎ 当方程组只有一个解时两函数图象只有一个交点；‎ 当方程组无解时两函数图象没有交点.‎ 知能解读(二)二次函数与一元二次方程的关系 函数，当时，得到一次方程，那么一元二次方程的根就是二次函数的图象与轴交点的横坐标，因此，二次函数的图象与x轴的交点情况决定相应一元二次方程根的情况.‎ ‎(1)当二次函数的图象与轴有两个交点时，，方程有两个不相等的实数根；‎ ‎(2)当二次函数的图象与轴有且只有一个交点时，，方程有两个相等的实数根；‎ ‎(3)当二次函数的图象与轴无交点时，，方程无实数根.‎ 综上，求一元二次方程的根也就是求二次函数的值为0时自变量的值，即抛物线与轴的交点的横坐标.二次函数的图象与轴的交点的三种情况分别对应着一元二次方程的根的三种情况，如下表所示：‎ 的取值 二次函数的图象与轴的交点 有两个交点 有一个交点 无交点 有两个交点 有一个交点 无交点 一元二次方程的实数根 有两个不相等的实数根 有两个相等的实数根 没有实数根 注意 若抛物线与轴的交点为和，则抛物线的对称轴为直线，对称轴与轴的交点恰为线段的中点.‎ 知能解读(三)二次函数与一元二次不等式的关系(拓展点)‎ 抛物线在轴上方的部分点的纵坐标为正，所对应的的所有值就是不等式的解集；在轴下方的部分点的纵坐标都为负，所对应的的所有值就是不等式的解集，不等式中如果带有等号其解集也相应带有等号.‎ 二次函数与一元二次不等式及之间的关系如下：‎ 的取值 抛物线与轴的交点 有两个交点 有一个交点 无交点 不等式的解集 或 ‎（或）‎ 全体实数 不等式的解集 无解 无解 抛物线与轴的交点 有两个交点 有一个交点 无交点 不等式的解集 无解 无解 不等式的解集 或 或（或）‎ 全体实数 知能解读(四)二次函数在实际问题中的应用 函数的应用指的是运用函数概念建立函数模型，研究、解决某些实际问题的过程和方法，它包括两个方面：‎ ‎(1)用二次函数表示实际问题中变量之间的关系；‎ ‎(2)用二次函数解决实际问题中的最优化问题，其实质就是求函数的最大(小)值.‎ 注意 ‎(1)优化问题，即求二次函数何时达到最大(小)值，此时需注意顶点的横坐标是否在实际问题中的取值范围内.‎ ‎⑵已知函数值，求自变量的对应值.特别地，：求抛物线与轴交点的横坐标，这些可以通过解一元二次方程解决，但要注意检验方程的解是否符合实际问题的要求.‎ 方法技巧归纳 方法技巧(一)求两函数图象交点问题的方法 两函数图象交点的横坐标和纵坐标就是两函数解析式所组成的方程组的解.‎ 方法技巧(二)二次函数与一元二次方程关系的综合应用 主要依据判别式的符号来判断，即当时，抛物线与轴有两个不同的交点；当时，抛物线与轴有一个交点；当时，抛物线与轴无交点.‎ 方法技巧(三)利用二次函数图象求不等式解集的方法(拓展)‎ 方法技巧(四)利用二次函数解决实际问题的方法 利用二次函数解决实际问题通常先要建立变量之间的二次函数解析式，再利用二次函数的相关性质求解.‎ 方法技巧(五)与二次函数相关的综合题 易混易错辨析 易混易错知识 二次函数配方为顶点式与用配方法解一元二次方程混淆.‎ 易混易错(一)实际问题中忽视自变量取值范围致错 易混易错(二)忽视二次项系数不为0致错 中考试题研究 中考命题规律 在近几年的中考中，各地对应用函数知识解决生活中的问题及二次函数与方程、一次函数、反比例函数、几何图形的综合运用考查较多.中考中的压轴题多与二次函数相结合，尤其是二次函数的应用题是考查二次函数的主流题目.题型有填空题、选择题、解答题，主要以贴近生产生活、反映时代热点的图象信息题、阅读理解题、开放探究题等为主.利用二次函数最值解决实际问题已成为中考的热点，这也是二次函数知识的创新点，应予以关注.‎ 中考试题(一)由图象获取信息 中考试题(二)二次函数与一元二次方程 中考试题(三)应用二次函数知识解决实际问题 中考试题(四)解决抛物线型问题