2010年北京市密云县中考数学试题 13页

密云县2010年初中毕业考试 数 学 试 题 一、选择题（本题共32分，每小题4分）‎ ‎1．－3的绝对值等于（ ）‎ A．3 B． C．－ D．－3‎ ‎2．国家体育场“鸟巢”的座席数是91000个，这个数用科学记数法表示应为（ ）‎ A．0.91×103 B．9.1×‎103 ‎‎ C．91×103 D．9.1×104‎ ‎3．如图所示的几何体是由一些小立方块搭成的，则这个几何体的俯视图是（ ）‎ A．‎ B．‎ Ｃ．‎ D．‎ ‎4．若两圆的半径分别是‎1cm和‎5cm，圆心距为‎6cm，则这两圆的位置关系是（ ）‎ A．内切 B．相交 C．外切 D．外离 ‎5．众志成城，抗旱救灾．某小组7名同学积极捐水支援贵州旱区某中学，他们捐水的数额分别是(单位：瓶)：50，20，50，30，50，25，35．这组数据的众数和中位数分别是（ ）‎ A．50，20 B．50，‎30 C．50，35 D．35，50‎ ‎2‎ ‎3‎ ‎5‎ ‎3‎ ‎2‎ 图1‎ 图2‎ ‎6．有5张写有数字的卡片(如图1)，它们的背面都相同，现将它们背面朝上(如图2)，从中翻开任意一张是数字2的概率是（ ）‎ A． B． C． D． ‎7．一个多边形的内角和是外角和的2倍，则这个多边形的边数为（ ）‎ A．4 B．‎5 C．6 D．7‎ ‎8．下面是按一定规律排列的一列数：‎ 第1个数：－；‎ 第2个数：－；‎ 第3个数：－；‎ ‎……‎ 第n个数：－…．‎ 那么，在第10个数、第11个数、第12个数、第13个数中，最大的数是（ ）‎ C A E D B A．第10个数 B．第11个数 C．第12个数 D．第13个数 二、填空题（本题共16分，每小题4分）‎ ‎9．使有意义的x的取值范围是 ．‎ ‎10．分解因式：a3－ab2＝ ．‎ ‎11．如图，在△ABC中，D、E分别是AB、AC的中点，若DE＝‎2cm，则BC＝ cm．‎ ‎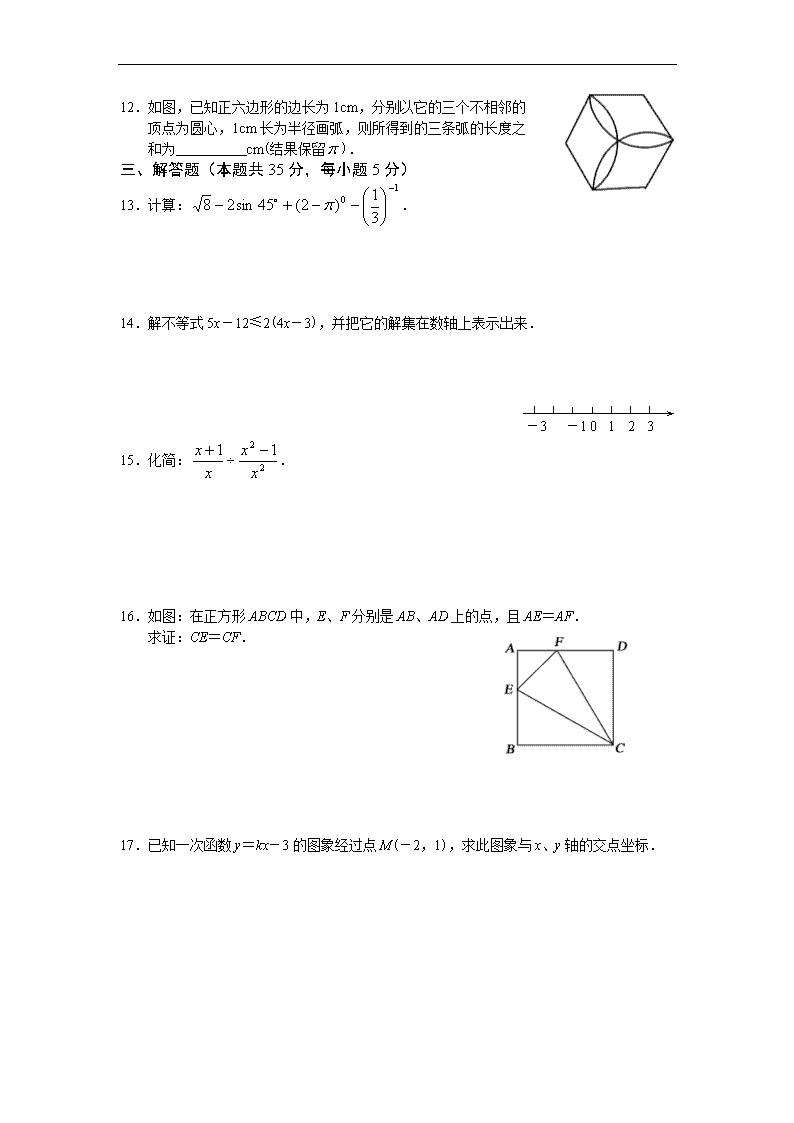12．如图，已知正六边形的边长为‎1cm，分别以它的三个不相邻的 顶点为圆心，‎1cm长为半径画弧，则所得到的三条弧的长度之 和为 cm(结果保留)．‎ 三、解答题（本题共35分，每小题5分）‎ ‎13．计算：．‎ ‎14．解不等式5x－12≤2(4x－3)，并把它的解集在数轴上表示出来．‎ ‎1‎ ‎2‎ ‎3‎ ‎0‎ ‎－1‎ ‎－3‎ ‎15．化简：．‎ ‎16．如图：在正方形ABCD中，E、F分别是AB、AD上的点，且AE＝AF．‎ 求证：CE＝CF．‎ ‎17．已知一次函数y＝kx－3的图象经过点M(－2，1)，求此图象与x、y轴的交点坐标．‎ A B C D ‎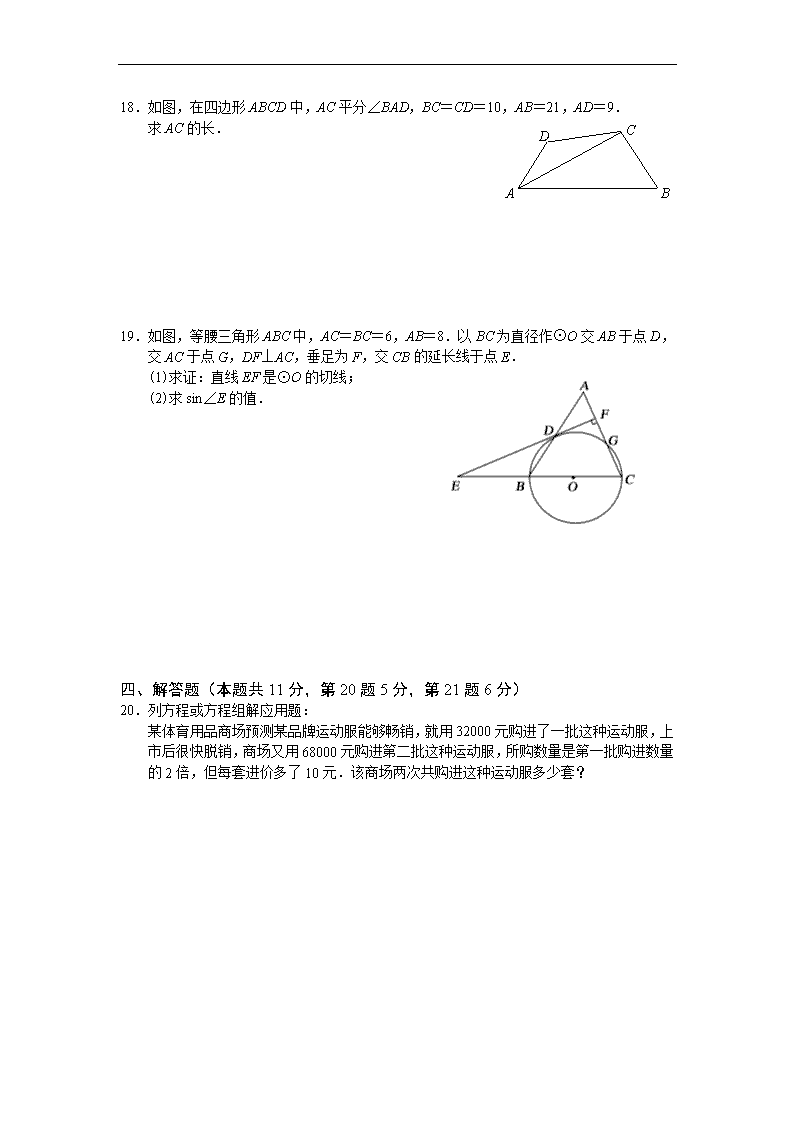18．如图，在四边形ABCD中，AC平分∠BAD，BC＝CD＝10，AB＝21，AD＝9．‎ 求AC的长．‎ ‎19．如图，等腰三角形ABC中，AC＝BC＝6，AB＝8．以BC为直径作⊙O交AB于点D，交AC于点G，DF⊥AC，垂足为F，交CB的延长线于点E．‎ ‎(1)求证：直线EF是⊙O的切线；‎ ‎(2)求sin∠E的值．‎ 四、解答题（本题共11分，第20题5分，第21题6分）‎ ‎20．列方程或方程组解应用题：‎ 某体育用品商场预测某品牌运动服能够畅销，就用32000元购进了一批这种运动服，上市后很快脱销，商场又用68000元购进第二批这种运动服，所购数量是第一批购进数量的2倍，但每套进价多了10元．该商场两次共购进这种运动服多少套？‎ ‎21‎ ‎．为了比较市场上甲、乙两种电子钟每日走时误差的情况，从这两种电子钟中，各随机抽取10台进行测试，两种电子钟走时误差的数据如下表(单位：秒)：‎ ‎ 编号 类型 一 二 三 四 五 六 七 八 九 十 甲种电子钟 ‎1‎ ‎－3‎ ‎－4‎ ‎4‎ ‎2‎ ‎－2‎ ‎2‎ ‎－1‎ ‎－1‎ ‎2‎ 乙种电子钟 ‎4‎ ‎－3‎ ‎－1‎ ‎2‎ ‎－2‎ ‎1‎ ‎－2‎ ‎2‎ ‎－2‎ ‎1‎ ‎(1)计算甲、乙两种电子钟走时误差的平均数；‎ ‎(2)计算甲、乙两种电子钟走时误差的方差；‎ ‎(3)根据经验，走时稳定性较好的电子钟质量更优．若两种类型的电子钟价格相同，请问：你用哪种电子钟？为什么？‎ 五、解答题（本题共4分）‎ ‎22．(1)观察与发现：‎ A C D B 图①‎ A C D B 图②‎ F E 在一次数学课堂上，老师把三角形纸片ABC(AB＞AC)沿过A点的直线折叠，使得AC落在AB边上，折痕为AD，展开纸片(如图①)；再次折叠该三角形纸片，使点A和点D重合，折痕为EF，展平纸片后得到△AEF(如图②)．有同学说此时的△AEF是等腰三角形，你同意吗？请说明理由．‎ ‎(2)实践与运用 E DD C F B A 图③‎ E D C A B F G A D E C B F G 图④‎ 图⑤‎ 将矩形纸片ABCD沿过点B的直线折叠，使点A落在BC边上的点F处，折痕为BE(如图③)；再沿过点E的直线折叠，使点D落在BE上的点处，折痕为EG(如图④)；再展平纸片(如图⑤)．试问：图⑤中∠的大小是多少？(直接回答，不用说明理由)．‎ 六、解答题（本题共22分，第23题7分，第24题7分，第25题8分）‎ ‎23．已知：如图，正比例函数y＝ax的图象与反比例函数y＝的图象交于点A(3，2)．‎ ‎(1)试确定上述正比例函数和反比例函数的表达式；‎ ‎(2)根据图象回答，在第一象限内，当x取何值时，反比例函数的值大于正比例函数的值？‎ ‎(3)M(m，n)是反比例函数图象上的一动点，其中0＜m＜3过点M作直线MB∥x轴，交y轴于点B；过点A作直线AC∥y轴交x轴于点C，交直线MB于点D．当四边形OADM的面积为6时，请判断线段BM与DM的大小关系，并说明理由．‎ ‎24．如图，将腰长为的等腰Rt△ABC(∠C是直角)放在平面直角坐标系中的第二象限，其中点A在y轴上，点B在抛物线y＝ax2＋ax－2上，点C的坐标为(－1，0)．‎ ‎(1)点A的坐标为 ，点B的坐标为 ；‎ ‎(2)抛物线的关系式为 ，其顶点坐标为 ；‎ ‎(3)将三角板ABC绕顶点A逆时针方向旋转90°，到达的位置．请判断点、是否在(2)中的抛物线上，并说明理由．‎ ‎25．如图，在梯形ABCD中，AD∥BC，AD＝3，CD＝5，BC＝10，梯形的高为4．动点M从B点出发沿线段BC以每秒2个单位长度的速度向终点C运动；动点N同时从C点出发沿线段CD以每秒1个单位长度的速度向终点D运动．设运动的时间为t(秒)．‎ ‎(1)当MN∥AB时，求t的值；‎ ‎(2)试探究：t为何值时，△CMN为等腰三角形．‎ ‎2010年密云县初中毕业考试 数学试卷答案参考及评分标准 一、选择题(本题共32分，每小题4分)‎ 题 号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 答 案 A D D C C B C A 二、填空题(本题共16分，每小题4分)‎ 题 号 ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答 案 x≥1‎ ‎4‎ ‎2π 三、解答题(本题共35分，每小题5分)‎ ‎13．(本小题满分5分)‎ 解：‎ ‎ 4分 ‎． 5分 ‎14．(本小题满分5分)‎ 解：去括号，得． 1分 移项，得． 2分 合并，得． 3分 系数化为1，得． 4分 不等式的解集在数轴上表示如图： ‎ ‎1‎ ‎2‎ ‎3‎ ‎0‎ ‎ ‎ ‎ ‎ ‎ 5分 ‎ ‎ ‎15．(本小题满分5分)‎ 解：原式 3分 ‎ ． 5分 ‎16．(本小题满分5分)‎ 证明：在正方形ABCD中，‎ 知AB=AD=DC=BC，∠B=∠D=90O．-------------------------------------------------2分 ‎∵ AE=AF，‎ ‎∴ AB-AE=AD-AF．‎ 即 BE=DF． 3分 在△BCE和△DCF中，‎ ‎∴ △BCE≌△DCF． 4分 ‎∴ CE＝CF． 5分 ‎17．(本小题满分5分)‎ 解：∵ 一次函数的图象经过点， ‎ ‎∴ ． 1分 解得 ． 2分 ‎∴ 此一次函数的解析式为． 3分 令，可得．‎ ‎∴ 一次函数的图象与轴的交点坐标为． 4分 令，可得．‎ ‎∴ 一次函数的图象与轴的交点坐标为． 5分 ‎18．(本小题满分5分)‎ 解：如图，∵ AC平分∠BAD，‎ ‎∴ 把△ADC沿AC翻折得△AEC，‎ ‎∴ AE=AD=9，CE=CD=10=BC．------------------------------------------------------2分 作CF⊥AB于点F．∴ EF=FB=BE=(AB-AE)=6．------------------------3分 在Rt△BFC(或Rt△EFC)中，由勾股定理得 CF=8．----------------------------4分 在Rt△AFC中，由勾股定理得 AC=17．‎ ‎∴ AC的长为17． -------------------------------------------------------------------------5分 ‎19． (本小题满分5分)‎ ‎(1)证明：如图，连结，则 ．‎ ‎∴ ．‎ ‎ ∵ AC=BC, ∴ ．‎ ‎ ∴ ．‎ ‎ ∵ ∥，∴ ．‎ ‎ ∵ 于F，∴ ．‎ ‎∴．∴ ．‎ ‎∴ EF是⊙O的切线． ------------------------------------------------------------3分 ‎( 2 ) 连结BG，∵BC是直径, ∴∠BGC=90=∠CFE．‎ ‎ ∴ BG∥EF．∴ ．‎ ‎ 设 ，则 ．‎ ‎ 在Rt△BGA中,．‎ 在Rt△BGC中, ．‎ ‎∴ ．解得 ．即 ．‎ 在Rt△BGC中, ．‎ ‎∴ sin∠E． --------------------------------------------- --------------------------------5分 四、解答题(本题共11分，第20题5分，第21题6分)‎ ‎20．(本小题满分5分)‎ 解：设商场第一次购进套运动服，‎ 由题意得： ． 3分 解这个方程，得．‎ 经检验，是所列方程的根．‎ ‎．‎ 答：商场两次共购进这种运动服600套． 5分 ‎21．(本小题满分6分)‎ 解：(1)甲种电子钟走时误差的平均数是：‎ ‎；‎ 乙种电子钟走时误差的平均数是：‎ ‎．‎ ‎∴ 两种电子钟走时误差的平均数都是0秒． --------------------------------- 2分 ‎(2)；‎ ‎．‎ ‎∴ 甲乙两种电子钟走时误差的方差分别是6s2和4．8s2．---------------------------4分 ‎(3)我会用乙种电子钟，因为平均水平相同，且甲的方差比乙的大，说明乙的稳定性更好，故乙种电子钟的质量更优． -----------------------------------------6分 五、解答题(本题共4分)‎ ‎22．(本小题满分4分)‎ 解：(1)同意．如图，设AD与EF交于点M，‎ 由折叠知，∠BAD=∠CAD，‎ ‎∠AME=∠AMF=90O． ------------------------------1分 ‎ ∴ 根据三角形内角和定理得 ‎ ‎∠AEF=∠AFE． ------------------------------------2分 ‎ ∴ △AEF是等腰三角形． 3分 ‎(2)图⑤中的大小是22．5o． 4分 六、解答题(本题共22分，第23题7分，第24题7分，第25题8分)‎ ‎23．(本小题满分7分)‎ 解：(1)将分别代入中，‎ 得，‎ ‎ ∴ ．‎ ‎ ∴ 反比例函数的表达式为：；‎ ‎ 正比例函数的表达式为． 2分 ‎ (2)观察图象得，在第一象限内，当时，‎ 反比例函数的值大于正比例函数的值．--------------------------------------------4分 ‎(3)．‎ ‎ 理由：∵ ，‎ ‎ ∴ ．‎ ‎ 即 ．‎ ‎ ∵ ，‎ ‎∴ ．‎ 即 ．‎ ‎∴ ．‎ ‎∴ ．‎ ‎∴． 7分 ‎24．(本小题满分7分)‎ 解：(1)A(0，2)， B(，1)． 2分 ‎(2)解析式为； 3分 顶点为()． 4分 ‎(3)如图，过点作轴于点M，过点B作轴于点N，过点作 ‎ 轴于点P．‎ 在Rt△AB′M与Rt△BAN中，‎ ‎∵ AB=AB′， ∠AB′M=∠BAN=90°-∠B′AM，‎ ‎∴ Rt△AB′M≌Rt△BAN．‎ ‎∴ B′M=AN=1，AM=BN=3， ∴ B′(1，)．‎ 同理△AC′P≌△CAO，C′P=OA=2，AP=OC=1，‎ 可得点C′(2，1)；‎ 将点B′、C′的坐标代入，‎ 可知点B′、C′在抛物线上． 7分 ‎(事实上，点P与点N重合)‎ ‎ 25．(本小题满分8分)‎ 解：(1)如图①，过作交于点，则四边形是平行四边形．‎ ‎∵ ，∴ ．‎ ‎∴ ．‎ ‎∴ ．‎ 由题意知，当、运动到秒时，‎ ‎∵ ，∴ ．‎ ‎∴ ．即 ．‎ 解得，． 5分 ‎(3)分三种情况讨论：‎ ‎① 当时，如图②，即．‎ ‎∴ ． 6分 ‎② 当时，如图③，过作于，于H．‎ 则 ，．‎ ‎∴ ．‎ ‎∵ ，∴ ．‎ ‎∴ ．即 ．‎ ‎∴ ． 7分 ‎③ 当时，如图④，过作于点．‎ 则 ．‎ ‎∵，‎ ‎∴ ．‎ ‎∴ ．即 ．‎ ‎∴ ． --------------------------------------------------------------------------8分 综上所述，当、或时，为等腰三角形．‎