浙江丽水市2013中考数学卷 9页

‎2013浙江丽水中考数学试题 一、选择题（本题有10小题，每小题3分，共30分）‎ ‎1. 在数0，2，-3，-1.2中，属于负整数的是 A. 0 B. 2 C. -3 D. -1.2‎ ‎2. 化简的结果是 A. B. C. D. ‎ ‎3. 用3个相同的立方块搭成的几何体如图所示，则它的主视图是 ‎4. 若关于的不等式组的解表示在数轴上如图所示，则这个不等式组的解释 A. ≤2 B. >1‎ C. 1≤<2 D. 1<≤2‎ ‎5. 如图，AB∥CD，AD和BC相交于点O，∠A=20°，‎ ‎∠COD=100°，则∠C的度数是 A. 80° B. 70°‎ C. 60° D. 50° ‎ ‎6. 王老师对本班40名学生的血型作了统计，列出如下的统计表，则本班A型血的人数是 A. 16人 B. 14人 C. 4人 D. 6人 ‎7. 一元二次方程可转化为两个一元一次方程，其中一个一元一次方程是，则另一个一元一次方程是 A. B. C. D. ‎ ‎8. 一条排水管的截面如图所示，已知排水管的半径OB=10，水面宽AB=16，则截面圆心O到水面的距离OC是 A. 4 B. 5 C. 6 D. 8‎ ‎9. 若二次函数的图象经过点P（-2，4），则该图象必经过点 A. （2，4） B. （-2，-4） C. （-4，2） D. 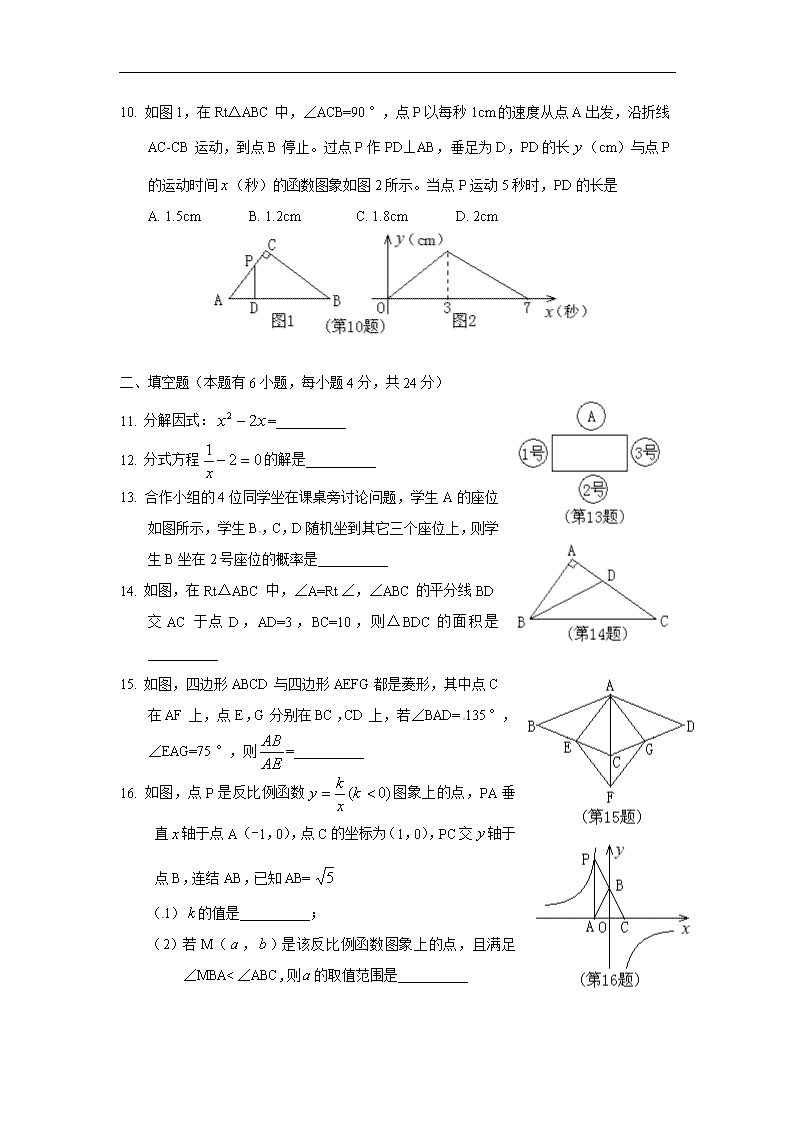（4，-2）‎ ‎10. 如图1，在Rt△ABC中，∠ACB=90°，点P以每秒1cm的速度从点A出发，沿折线AC-CB运动，到点B停止。过点P作PD⊥AB，垂足为D，PD的长（cm）与点P的运动时间（秒）的函数图象如图2所示。当点P运动5秒时，PD的长是 A. 1.5‎cm B. 1.2cm C. 1.8cm D. 2cm 二、填空题（本题有6小题，每小题4分，共24分）‎ ‎11. 分解因式：=__________‎ ‎12. 分式方程的解是__________‎ ‎13. 合作小组的4位同学坐在课桌旁讨论问题，学生A的座位如图所示，学生B，C，D随机坐到其它三个座位上，则学生B坐在2号座位的概率是__________‎ ‎14. 如图，在Rt△ABC中，∠A=Rt∠，∠ABC的平分线BD交AC于点D，AD=3，BC=10，则△BDC的面积是__________‎ ‎15. 如图，四边形ABCD与四边形AEFG都是菱形，其中点C 在AF上，点E，G分别在BC，CD上，若∠BAD=135°，∠EAG=75°，则=__________‎ ‎16. 如图，点P是反比例函数图象上的点，PA垂直轴于点A（-1，0），点C的坐标为（1，0），PC交轴于点B，连结AB，已知AB=‎ ‎（1）的值是__________；‎ ‎（2）若M（，）是该反比例函数图象上的点，且满足∠MBA<∠ABC,则的取值范围是__________‎ 三、解答题（本题有8小题，共66分，各题必须写出解答过程）‎ ‎17.（本题6分）‎ 计算：‎ ‎18.（本题6分）‎ 先化简，再求值：，其中 ‎19.（本题6分）‎ 一个长方体木箱沿斜面下滑，当木箱滑至如图位置时，AB=3m，已知木箱高BE=m，斜面坡角为30°，求木箱端点E距地面AC的高度EF。‎ ‎20.（本题分）‎ 如图，科技小组准备用材料围建一个面积为60m2的矩形科技园ABCD，其中一边AB靠墙，墙长为12m，设AD的长为m，DC的长为m。‎ ‎（1）求与之间的函数关系式；‎ ‎（2）‎ 若围成矩形科技园ABCD的三边材料总长不超过26m，材料AD和DC的长都是整米数，求出满足条件的所有围建方案。‎ ‎21.（本题8分）‎ 如图，在△ABC中，AB=AC，∠BAC=54°，以AB为直径的⊙O分别交AC，BC于点D，E，过点B作⊙O的切线，交AC的延长线于点F。‎ ‎（1）求证：BE=CE；‎ ‎（2）求∠CBF的度数；‎ ‎（3）若AB=6，求的长。‎ ‎22.（本题10分）‎ 本学期开学初，学校体育组对九年级某班50名学生进行了跳绳项目的测试，根据测试成绩制作了下面两个统计图。‎ 根据统计图解答下列问题：‎ ‎（1）本次测试的学生中，得4分的学生有多少人？‎ ‎（2）本次测试的平均分是多少？‎ ‎（3）通过一段时间的训练，体育组对该班学生的跳绳项目进行第二次测试，测得成绩的最低分为3分，且得4分和5分的人数共有45人，平均分比第一次提高了0.8分，问第二次测试中，得4分、5分的学生分别有多少人？‎ ‎23.（本题10分）‎ 如图，已知抛物线与直线交于点O（0，0），A（，12），点B是抛物线上O，A之间的一个动点，过点B分别作轴、轴的平行线与直线OA交于点C，E。‎ ‎（1）求抛物线的函数解析式；‎ ‎（2）若点C为OA的中点，求BC的长；‎ ‎（3）以BC，BE为边构造矩形BCDE，设点D的坐标为（，），求出，之间的关系式。‎ ‎24.（本题12分）‎ 如图1，点A是轴正半轴上的动点，点B坐标为（0，4），M是线段AB的中点，将点M绕点A顺时针方向旋转90°得到点C，过点C作轴的垂线，垂足为F，过点B作轴的垂线与直线CF相交于点E，点D点A关于直线CF的对称点，连结AC，BC，CD，设点A的横坐标为 ‎（1）当时，求CF的长；‎ ‎（2）①当为何值时，点C落在线段BD上？‎ ‎②设△BCE的面积为S，求S与之间的函数关系式；‎ ‎（3）如图2，当点C与点E重合时，△CDF沿轴左右平移得到△C’D’F’，再将A，B，C’，D’为顶点的四边形沿C’F’剪开，得到两个图形，用这两个图形拼成不重叠且无缝隙的图形恰好是三角形，请直接写出所有符合上述条件的点C’的坐标。‎