新修订版全国各地中考数学试题分类汇编考点34相似形及应用含答案 31页

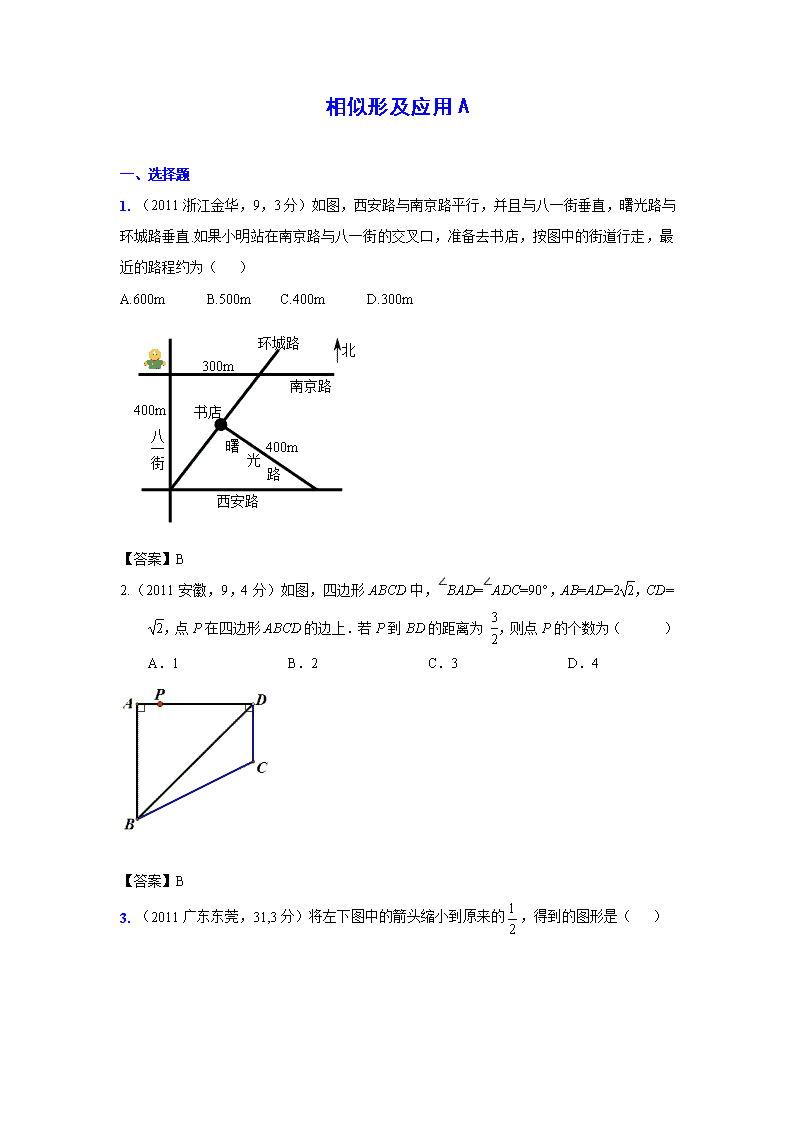
相似形及应用A 一、选择题 ‎1. （2011浙江金华，9，3分）如图，西安路与南京路平行，并且与八一街垂直，曙光路与环城路垂直.如果小明站在南京路与八一街的交叉口，准备去书店，按图中的街道行走，最近的路程约为（ ）‎ A‎.600m B‎.500m C‎.400m D‎.300m ‎【答案】B ‎2.（2011安徽，9，4分）如图，四边形ABCD中，∠BAD=∠ADC=90°，AB=AD=2，CD=，点P在四边形ABCD的边上．若P到BD的距离为 ，则点P的个数为（ ）‎ A．1 B．‎2 ‎ C．3 D．4‎ ‎【答案】B ‎ ‎3. （2011广东东莞，31,3分）将左下图中的箭头缩小到原来的，得到的图形是（ ）‎ ‎【答案】Ａ ‎ ‎4. （2011浙江省，6，3分）如图，直角三角形纸片的两直角边长分别为6、8，按如图那样折叠，使点A与点B重合，折痕为DE，则S△BCE：S△BDE等于（ ）‎ ‎ A. 2：5 B.14:‎25 C.16:25 D. 4:21‎ ‎【答案】B ‎5. （2011浙江台州，5,4分）若两个相似三角形的面积之比为1:4，则它们的周长之比为（ ）‎ A. 1:2 B. 1:‎4 C. 1:5 D. 1:16‎ ‎【答案】A ‎6. （2011浙江省嘉兴，7，4分）如图，边长为4的等边△ABC中，DE为中位线，则四边形BCED的面积为（　　）‎ ‎（A） （B） （C） （D）‎ ‎（第7题）‎ ‎【答案】B ‎7. （2011浙江丽水，9，3分）如图，西安路与南京路平行，并且与八一街垂直，曙光路与环城路垂直.如果小明站在南京路与八一街的交叉口，准备去书店，按图中的街道行走，最近的路程约为（ ）‎ A‎.600m B‎.500m C‎.400m D‎.300m ‎8. （2011台湾台北，26）图(十)为一，其中D、E两点分别在、上，且＝31，＝29，＝30，＝32。若，则图中、、、的大小关系，下列何者正确？‎ A．＞ B．＝ C．＞ D．＝‎ ‎【答案】D ‎9. （2011甘肃兰州，13，4分）现给出下列四个命题：①无公共点的两圆必外离；②位似三角形是相似三角形；③菱形的面积等于两条对角线的积；④对角线相等的四边形是矩形。‎ 其中真命题的个数是 A．1 B．‎2 ‎ C．3 D．4‎ ‎【答案】A ‎10．（2011山东聊城，11，3分）如图，在直角坐标系中，矩形OABC的顶点O在坐标原点，边OA在x轴上，OC在y轴上，如果矩形OA′B′C′与矩形OABC关于点O位似，且矩形OA′B′C′的面积等于矩形OABC面积的，那么点B′的坐标是（ ）‎ ‎ ‎ A．（3，2） B．（－2，－3） ‎ C．（2，3）或（－2，－3） D．（3，2）或（－3，－2）‎ ‎【答案】D ‎11. （2011广东汕头，31,3分）将左下图中的箭头缩小到原来的，得到的图形是（ ）‎ ‎【答案】Ａ ‎12. （2011四川广安，7，3分）下列命题中，正确的是（ ） ‎ ‎ A．过一点作已知直线的平行线有一条且只有一条 ‎ B．对角线相等的四边形是矩形 ‎ C．两条边及一个角对应相等的两个三角形全等 ‎ D．位似图形一定是相似图形 ‎【答案】D ‎ ‎13. （ 2011重庆江津， 8，4分）已知如图(1)、(2)中各有两个三角形,其边长和角的度数已在图上标注,图(2)中AB、CD交于O点,对于各图中的两个的两个三角形而言,下列说法正确的是( )‎ A.都相似 B.都不相似 C.只有(1)相似 D.只有(2)相似 ‎35°‎ ‎75°‎ ‎75°‎ ‎70°‎ ‎(1)‎ A B C D O ‎4‎ ‎3‎ ‎6‎ ‎8‎ ‎(2)‎ 第8题图 ‎【答案】A·‎ ‎14. (2011重庆綦江，4，4分)若相似△ABC与△DEF的相似比为1 ：3，则△ABC与△DEF的面积比为（ ）‎ ‎ A．1 ：3 B．1 ：‎9 C．3 ：1 D． 1 ：‎ ‎【答案】：B ‎ ‎15. （2011山东泰安，15 ，3分）如图，点F是□ABCD的边CD上一点，直线BF交AD的延长线于点E，则下列结论错误的是 A.= B.= C. = D.= ‎【答案】C ‎ ‎16. （2011山东潍坊，3，3分）如图，△ABC中，BC = 2，DE是它的中位线，下面三个结论：⑴DE=1；⑵△ADE∽△ABC；⑶△ADE的面积与△ABC的面积之比为 1 : 4。其中正确的有（ ）‎ A . 0 个 B.1个 C . 2 个 D.3个 ‎【答案】D ‎17. （2011湖南怀化，6，3分）如图3所示：△ABC中，DE∥BC，AD=5，BD=10，AE=3，‎ 则CE的值为 ‎ A.9 B‎.6 ‎‎ C.3 D.4‎ ‎【答案】B ‎18. （2011江苏无锡，7，3分）如图，四边形ABCD的对角线AC、BD相交于O，且将这个四边形分成①、②、③、④四个三角形．若OA∶OC = OB∶OD，则下 列结论中一定正确的是 ( )‎ A．①和②相似 B．①和③相似 C．①和④相似 D．②和④相似 A B C D O ‎①‎ ‎②⊙o⊙‎ ‎③⊙o⊙‎ ‎④⊙o⊙‎ ‎（第7题）‎ ‎【答案】B ‎19. （2011广东肇庆，5，3分）如图，已知直线a∥b∥c，直线m、n 与a、b、c分别交于点A、C、E、B、D、F，AC ＝ 4，CE ＝ 6，BD ＝ 3，则BF ＝‎ a b c A B C D E F m n A． 7 B． ‎7.5 ‎C． 8 D． 8.5‎ ‎【答案】B ‎20．（2011湖南永州，12，3分）下列说法正确的是（ ）‎ A．等腰梯形的对角线互相平分． ‎ B．一组对边平行，另一组对边相等的四边形是平行四边形．‎ C．线段的垂直平分线上的点到线段两个端点的距离相等．‎ D．两边对应成比例且有一个角对应相等的两个三角形相似．‎ ‎【答案】C ‎21. （2011山东东营，11，3分）如图，△ABC中，A，B两个顶点在x轴的上方，点C的坐标是(-1，0)．以点C为位似中心，在x轴的下方作△ABC的位似图形△A′B′C，并把△ABC的边长放大到原来的2倍．设点B的对应点B′的横坐标是a，则点B的横坐标是（ ）‎ A． B．‎ C． D．‎ B′‎ A′‎ 第11题 ‎-1‎ x ‎1‎ O ‎-1‎ ‎1‎ y B A C ‎【答案】D ‎22. （2011重庆市潼南,5,4分）若△ABC～△DEF，它们的面积比为4：1，则△ABC与△DEF的相似比为 A．2：1 B．1 ：‎2 ‎‎ ‎ 　 C．4：1 D．1：4‎ ‎【答案】A ‎23. （2011广东中山，3,3分）将左下图中的箭头缩小到原来的，得到的图形是（ ）‎ ‎【答案】Ａ ‎24. （2011湖北荆州，7，3分）如图，P为线段AB上一点，AD与BC交于E，∠CPD＝∠A＝∠B，BC交PD于F，AD交PC于G，则图中相似三角形有 A．1对　　B．2对　　　C．3对　　　　D．4对　‎ ‎　　第7题图 ‎【答案】C 二、填空题 ‎1. （2011广东广州市，14，3分）如图3，以点O为位似中心，将五边形ABCDE放大后得到五边形A′B′C′D′E′，已知OA=‎10cm，OA′=‎20cm，则五边形ABCDE的周长与五边形A′B′C′D′E′的周长的比值是 ．‎ 图3‎ O A B C D E A′‎ B′‎ C′‎ D′‎ E′‎ ‎【答案】 ‎2. （2011四川重庆，12，4分）如图，△ABC中，DE∥BC，DE分别交边AB、AC于D、E两点，若AD：AB＝1：3，则△ADE与△ABC的面积比为 ．‎ ‎【答案】1：9‎ ‎3. （2011江苏苏州，17,3分）如图，已知△ABC的面积是的等边三角形，△ABC∽△ADE，AB=2AD，∠BAD=45°，AC与DE相交于点F，则△AEF的面积等于__________（结果保留根号）.‎ ‎【答案】‎ 三、解答题 ‎1. （2011江西，25，10分）某数学兴趣小组开展了一次活动，过程如下：‎ 设∠BAC=（0°＜＜90°）.现把小棒依次摆放在两射线AB，AC之间，并使小棒两端分别落在两射线上.‎ 活动一：‎ 如图甲所示，从点A1开始，依次向右摆放小棒，使小棒与小棒在两端点处互相垂直，A‎1A2为第1根小棒.‎ 数学思考：‎ ‎（1）小棒能无限摆下去吗？答： .（填“能”或“不能”）‎ ‎（2）设AA1=A‎1A2=A‎2A3=1.‎ ‎①= 度；‎ ‎②若记小棒A2n‎-1A2n的长度为an（n为正整数，如A‎1A2=a1,A‎3A4=a2,）,求此时a2，a3的值，并直接写出an（用含n的式子表示）.‎ 活动二：‎ 如图乙所示，从点A1开始，用等长的小棒依次向右摆放，其中A‎1A2为第1根小棒，且A‎1A2= AA1.‎ 数学思考：‎ ‎（3）若已经向右摆放了3根小棒，则= ，= ，= ；（用含的式子表示）‎ ‎（4）若只能摆放4根小棒，求的范围.‎ ‎【答案】‎ ‎【答案】解：（1）能 ‎（2）①22.5°‎ ‎②方法一：‎ ‎∵AA1=A‎1A2=A‎2A3=1， A‎1A2⊥A‎2A3，∴A‎1A3=，AA3=1+.‎ 又∵A‎2A3⊥A‎3A4，∴A‎1A2∥A‎3A4.同理：A‎3A4∥A‎5A6，∴∠A=∠AA‎2A1=∠AA‎4A3=∠AA‎6A5，‎ ‎∴AA3=A‎3A4，AA5=A‎5A6，∴a2= A‎3A4=AA3=1+,a3=AA3+A‎3A5=a2+A‎3A5.∵A‎3A5=a2,‎ ‎∴a3=A‎5A6=AA5=a2+a2=(+1)2.‎ 方法二：‎ ‎∵AA1=A‎1A2=A‎2A3=1， A‎1A2⊥A‎2A3，∴A‎1A3=，AA3=1+.‎ 又∵A‎2A3⊥A‎3A4，∴A‎1A2∥A‎3A4.同理：A‎3A4∥A‎5A6，∴∠A=∠AA‎2A1=∠AA‎4A3=∠AA‎6A5，‎ ‎∴a2=A‎3A4=AA3=1+,又∵∠A‎2A3A4=∠A‎4A5A6=90°，∠A‎2A4A3=∠A‎4A6A5，∴△A‎2A3A4∽△A‎4A5A6，‎ ‎∴，∴a3==(+1)2.‎ an=(+1)n-1.‎ ‎(3)‎ ‎(4)由题意得，∴15°＜≤18°.‎ ‎2. （2011江苏宿迁,28,12分）如图，在Rt△ABC中，∠B＝90°，AB＝1，BC＝，以点C为圆心，CB为半径的弧交CA于点D；以点A为圆心，AD为半径的弧交AB于点E．‎ ‎　（1）求AE的长度；‎ ‎（2）分别以点A、E为圆心，AB长为半径画弧，两弧交于点F（F与C在AB两侧），连接AF、EF，设EF交弧DE所在的圆于点G，连接AG，试猜想∠EAG的大小，并说明理由．‎ ‎（第28题）‎ ‎【答案】‎ 解：（1）在Rt△ABC中，由AB＝1，BC＝得 AC＝＝‎ ‎ ∵BC＝CD，AE＝AD ‎∴AE＝AC－AD＝．‎ ‎ （2）∠EAG＝36°，理由如下：‎ ‎ ∵FA＝FE＝AB＝1，AE＝‎ ‎∴＝‎ ‎∴△FAE是黄金三角形 ‎∴∠F＝36°，∠AEF＝72°‎ ‎∵AE＝AG，FA＝FE ‎∴∠FAE＝∠FEA＝∠AGE ‎∴△AEG∽△FEA ‎∴∠EAG＝∠F＝36°．‎ ‎3. （2011广东汕头，21，9分）如图（1），△ABC与△EFD为等腰直角三角形，AC与DE重合，AB=EF=9，∠BAC＝∠DEF＝90°，固定△ABC，将△EFD绕点A 顺时针旋转，当DF 边与AB边重合时，旋转中止.不考虑旋转开始和结束时重合的情况，设DE、DF（或它们的延长线）分别交BC（或它的延长线）于G、H点，如图（2）.‎ ‎（1）问：始终与△AGC相似的三角形有 及 ；‎ ‎（2）设CG＝x，BH＝y，求y关于x的函数关系式（只要求根据2的情况说明理由）；‎ ‎（3）问：当x为何值时，△AGH是等腰三角形？‎ ‎【解】（1）△HGA及△HAB；‎ ‎ （2）由（1）可知△AGC∽△HAB ‎∴，即，‎ 所以，‎ ‎（3）当CG＜时，∠GAC=∠H＜∠HAC，∴AC＜CH ‎∵AG＜AC，∴AG＜GH 又AH＞AG，AH＞GH 此时，△AGH不可能是等腰三角形；‎ 当CG=时，G为BC的中点，H与C重合，△AGH是等腰三角形；‎ 此时，GC=，即x=‎ 当CG＞时，由（1）可知△AGC∽△HGA 所以，若△AGH必是等腰三角形，只可能存在AG=AH 若AG=AH，则AC=CG，此时x=9‎ 综上，当x=9或时，△AGH是等腰三角形．‎ ‎4. （2011湖南怀化，21，10分）如图8，△ABC,是一张锐角三角形的硬纸片，AD是边BC上的高，BC=‎40cm,AD=‎30cm,从这张硬纸片上剪下一个长HG是宽HE的2倍的矩形EFGH，使它的一边EF在BC上，顶点G、H分别在AC，AB上，AD与HG的交点为M.‎ (1) 求证：‎ (2) 求这个矩形EFGH的周长.‎ ‎【答案】‎ (1) 解：∵四边形EFGH为矩形 ‎ ∴EF∥GH ‎ ∴∠AHG=∠ABC ‎ 又∵∠HAG=∠BAC ‎ ∴ △AHG∽△ABC ∴ ‎ ‎（2）由（1）得设HE=x，则HG=2x，AM=AD-DM=AD-HE=30-x 可得，解得，x=12 ， 2x=24 ‎ 所以矩形EFGH的周长为2×（12+24）=‎72cm.‎ ‎5. （2011上海，25，14分）在Rt△ABC中，∠ACB=90°，BC=30，AB=50．点P是AB边上任意一点，直线PE⊥AB，与边AC或BC相交于E．点M在线段AP上，点N在线段BP上，EM=EN，sin∠EMP=．‎ ‎（1）如图1，当点E与点C重合时，求CM的长；‎ ‎（2）如图2，当点E在边AC上时，点E不与点A、C重合，设AP=x，BN=y，求y关于x的函数关系式，并写出函数的定义域；‎ ‎（3）若△AME∽△ENB（△AME的顶点A、M、E分别与△ENB的顶点E、N、B对应），求AP的长．‎ 图1 图2 备用图 ‎【答案】（1）∵∠ACB=90°，∴AC===40．‎ ‎∵S==,‎ ‎∴CP===24．‎ 在Rt△CPM中，∵sin∠EMP=，‎ ‎∴．‎ ‎∴CM===26．‎ ‎（2）由△APE∽△ACB，得，即，∴PE=．‎ 在Rt△MPE中，∵sin∠EMP=，∴．‎ ‎∴EM===．‎ ‎∴PM=PN===．‎ ‎∵AP+PN+NB=50，∴x++y =50．‎ ‎∴y =(0 < x < 32)．‎ ‎（3）‎ 第三问：由于给出对应顶点，那么解法一可以直接运用相似和三角比求出对应边长再列比例式求解。本题还可以通过角度之间的关系转换求解，个人认为从角度入手更加简洁直观方法如下： ‎ ‎①当点E在线段AC上时，‎ ‎△AME∽△ENB，．∵EM=EN，∴．设AP=x，由（2）知EM=，AM==，NB=．‎ ‎∴‎ 解得x1=22，x2=0（舍去）．‎ 即AP=22．‎ ‎② 当点E在线段BC上时，‎ 根据外角定理，△ACE∽△EPM，∴．∴CE==．设AP=x，易得BE=，∴CE=30．∴30=．解得x=42．即AP=42．‎ ‎∴AP的长为22或42．‎ ‎6. （2011四川绵阳25，14）‎ 已知△ABC是等腰直角三角形，∠A=90°，D是腰AC上的一个动点，过C作CE垂直于BD或BD的延长线，垂足为E,如图1.‎ ‎(1)若BD是AC的中线，如图2，求的值；‎ ‎(2)若BD是∠ABC的角平分线，如图3，求的值；‎ ‎(3)结合（1)、（2)，请你推断的值的取值范围（直接写出结论，不必证明），并探究的值能小于吗？若能，求出满足条件的D点的位置；若不能，请说明理由.‎ ‎【答案】(1)设AD=x,则AB=2x,根据勾股定理，可得BD=x,∵△ABD∽△CDE, ,可得CE=x,所以= ‎（2）设AD=x,根据角平分线定理，可知DC=x，AB=x+x,由 勾股定理可知BD= △ABD∽△CDE，,∴EC=,‎ =2,‎ ‎(3)由前面两步的结论可以看出，,所以这样的点是存在的，D在AC边的五等分点和点A之间 ‎7. （2011湖北武汉市，24，10分）（本题满分10分）‎ ‎（1）如图1，在△ABC中，点D，E，Q分别在AB，AC，BC上，且DE∥BC，AQ交DE于点P．求证：． ‎ ‎（2） 如图，在△ABC中，∠BAC=90°，正方形DEFG的四个顶点在△ABC的边上，连接AG，AF分别交DE于M，N两点．‎ ‎①如图2，若AB=AC=1，直接写出MN的长；‎ ‎ ②如图3，求证MN2=DM·EN．‎ ‎【答案】（1）证明：在△ABQ中，由于DP∥BQ，‎ ‎∴△ADP∽△ABQ，    ‎ ‎∴DP/BQ＝AP/AQ．‎ 同理在△ACQ中，EP/CQ＝AP/AQ．‎ ‎∴DP/BQ＝EP/CQ．‎ ‎（2） ．‎ ‎（3）证明：∵∠B＋∠C=90°，∠CEF＋∠C=90°．‎ ‎∴∠B=∠CEF，‎ 又∵∠BGD=∠EFC，‎ ‎∴△BGD∽△EFC．‎ ‎∴DG/CF＝BG/EF，‎ ‎∴DG·EF＝CF·BG 又∵DG＝GF＝EF，∴GF2＝CF·BG ‎ 由（1）得DM/BG＝MN/GF＝EN/CF∴（MN/GF）2＝(DM/BG)·(EN/CF)‎ ‎∴MN2＝DM·EN ‎8. （2011河北，20，8分）如图10，在6×8网格图中，每个小正方形边长均为1，点O和△ABC的顶点均在小正方形的顶点.‎ ‎（1）以O为位似中心，在网格图中作△A′B′C′和△ABC位似，且位似比为1︰2；‎ ‎（2）连接（1）中的AA′,求四边形AA′C′C的周长.（结果保留根号）‎ ‎【答案】（1）如下图.‎ ‎（2）四边形AA′C′C的周长=4+6‎ 相似形及应用B 一、选择题 ‎1. （2011贵州毕节，7，3分）两个相似多边形的面积比是，其中较小多边形周长为‎36cm，则较大多边形周长为( )‎ ‎ A．‎48cm B．‎54cm C．‎56cm D．‎‎64cm ‎【答案】A ‎2. （2011海南省，12，3分）如图3，在△ABC中，∠ACB=90°，CD⊥AB于点D，则图中相似三角形共有 A．1对 B．2对 C．3对 D．4对 图3‎ A B C D ‎【答案】C ‎3. （2011广东深圳，7,3分）如图2, 小正方形的边长均为1, 则下列图中的三角形(阴影部分)与△ABC相似的是( )‎ ‎【答案】B ‎4. （2011山西，11，2分）如图，△ABC中，AB=AC，点D、E分别是边AB、AC的中点，点G、F在BC边上，四边形DEFG是正方形.若DE=2㎝,则AC的长为（ ）‎ A． B. C. D. ‎ A ‎ B ‎ C ‎ D ‎ E ‎ F ‎ G ‎ 第11题 ‎【答案】D ‎5. （2011陕西，9,3分） 如图，在□ABCD中，E、F分别是AD、CD 边上的点，连接BE、AF，他们相交于点G，延长BE交CD的延长线于点H，则图中的相似三角形共有（ ）‎ A．2对 B．3对 C．4对 D．5对 ‎【答案】C ‎6. （2011北京市，4，4分） 如图，在梯形ABCD中，AD∥BC，对角线AC，BD相交于点O，若，，则的值为( ) ‎ A． B． C． D． ‎ ‎【答案】B ‎7. （2011贵州遵义，10，3分）如图，在直角三角形ABC中（∠C＝900）,放 置边长分别3,4,的三个正方形，则x的值为 A. 5 B. ‎6 ‎‎ C. 7 D. 12‎ ‎【答案】C ‎8. （2011广东肇庆，5，3分）如图，已知直线a∥b∥c，直线m、n 与a、b、c分别交于点A、C、E、B、D、F，AC ＝ 4，CE ＝ 6，BD ＝ 3，则BF ＝‎ a b c A B C D E F m n A． 7 B． ‎7.5 ‎C． 8 D． 8.5‎ ‎【答案】B ‎9. （2011年铜仁地区，10，4分）已知:如图2,在△ABC中,∠AED=∠B,则下列等式成立的是( ).‎ ‎ ‎ ‎ A. B. ‎ C. D.‎ ‎【答案】C ‎10．(2011四川雅安8，3分)已知线段AB=‎10cm，点C是线段AB的黄金分割点（AC＞BC），则AC的长为（ ）‎ A B C D ‎ ‎【答案】 C ‎11. (2011四川雅安9，3分)如图，D、E、F分别为△ABC 三边的中点，则下列说法中不正确的为（ ）‎ A △ADE∽△ABC B C D DF=EF ‎【答案】 D ‎12. （2011福建漳州，10，3分）如图，小李打网球时，球恰好打过网，且落在离网‎4m的位置上，则球拍击球的高度A为( )‎ A．‎0.6m B．‎1.2m C．‎1.3m D．‎‎1.4m ‎【答案】D ‎13. （2011贵州六盘水，9，3分）“标准对数视力表”对我们来说并不陌生，图3是视力表的一部分，其中最上面较大的“E”与下面四个较小“E”中的哪一个是位似图形（ ）‎ 标准对数视力表 ‎0.1‎ ‎4.0‎ ‎0.12‎ ‎4.1‎ ‎4.2‎ ‎0.15‎ ‎ ‎ ‎ 图3‎ ‎ A．左上 B．左下 C．右上 D．右下 ‎【答案】B 二、填空题 ‎1. （2011贵州毕节，17，5分）已知，则的值是 。‎ ‎【答案】2‎ ‎2. ‎ ‎（2011黑龙江省哈尔滨市，20，3分）如图，在Rt△ABC中，∠ACB=90°，点D是斜边AB的中点，DE⊥AC,垂足为E，若DE=2，CD=,则BE的长为 _。‎ ‎【答案】‎ ‎3. （2011黑龙江绥化，11，3分）如图，△ABC是边长为1的等边三角形，取BC边中点E，作ED∥AB，EF∥AC，得到四边形EDAF，它的面积记作；取BE边中点，作∥FB，∥EF，得到四边形，它的面积记作.照此规律作下去，则= .‎ ‎【答案】（或）‎ ‎4. （2011吉林，9，2分）如图，△ABC中，点D、E分别为AB、AC的中点，连接DE，线段BE、CD相交于点O，若OD＝2，则OC＝ ‎ ‎【答案】4‎ ‎5. （2011昭通，17，3）如图6所示，某班上体育课，甲、乙两名同学分别站在C、D 的位置时，乙的影子恰好在甲的影子里边，已知甲身高‎1.8米，乙身高‎1.5米，甲的影长是‎6米，则甲、乙同学相距________米。‎ A D C E B ‎ 图6‎ ‎【答案】1‎ ‎6. （2011年青海，11,2分）如图3，△ABC是一块锐角三角形的材料，边BC=‎120mm，高AD=‎80mm，要把它加工成正方形零件，使正方形的一边在BC上，其余两个顶点分别在AB、AC上，这个正方形零件的边长是 mm.‎ ‎【答案】48‎ ‎7. （2011广西百色，17,3分）如图，以O为位似中心，把五边形ABCDE的面积扩大为原来的4倍，得五边形，则OD∶= ‎ ‎【答案】：1：2‎ ‎9. （2011张家界，16，3分）在△ABC中，AB=8，AC=6，在△DEF中，DE=4，DF=3，要使△ABC与△DEF相似，则需添加的一个条件是 （写出一种情况即可）.‎ ‎【答案】如∠A=∠D ‎10．（2011贵州六盘水，17，4分）从美学角度来说，人的上身长与下身长之比为黄金比时，可以给人一种协调的美感。某女老师上身长约‎61.80cm，下身长约‎93.00cm，她要穿约________cm的高跟鞋才能达到黄金比的美感效果（精确到‎0.01cm）‎ ‎【答案】7.00（若写7不扣分）‎ 三、解答题 ‎1. （2011广东河源，16，7分)‎ ‎ 如图5，点P在平行四边形ABCD的CD边上，连结BP并延长与 AD的延长线交于点Q．‎ ‎ （1）求证：△DQP∽△CBP；‎ ‎ （2）当△DQP≌△CBP，且AB=8时，求DP的长．‎ ‎【答案】（1）∵四边形ABCD是平行四边形，∴AQ∥BC, ∴△DQP∽△CBP；‎ ‎（2）∵△DQP≌△CBP，∴DP=CP=CD, ∵AB=CD=8, ∴DP=4.‎ ‎2. （2011辽宁大连，25,12分）在△ABC中，∠A＝90°，点D在线段BC上，∠EDB＝∠C，BE⊥DE，垂足为E，DE与AB相交于点F．‎ ‎（1）当AB＝AC时，（如图13），‎ ‎①∠EBF＝_______°；‎ ‎②探究线段BE与FD的数量关系，并加以证明；‎ ‎（2）当AB＝kAC时（如图14），求的值（用含k的式子表示）．‎ 图13‎ 图14‎ ‎【答案】‎ ‎⑴当AB＝AC时，（如图13），‎ ‎①22.5；‎ ‎②；‎ 证明：延长BE至点P使得EP＝EB，连接PD交AB于Q ‎∴BP＝2EB ‎∵BE⊥DE ‎ ‎∴∠BED＝∠PED＝90°‎ ‎∵EP＝EB，DE＝DE ‎ ‎∴△BED≌△PED ‎∴‎ ‎∴‎ ‎∴AC∥PD ‎ ‎∴∠BQD＝∠A＝90° ‎ ‎∴∴QB＝QD ‎∴∠PQB＝90°‎ 在△PQB 与△FQD中 ‎ ‎∵∠PQB＝∠FQD，QB＝QD，∠PBQ＝∠FDQ，‎ ‎∴△PQB≌△FQD ‎ ‎∴PB＝FD ＝2BE ‎ ‎∴‎ ‎⑵‎ 证明：延长BE至点P使得EP＝EB，连接PD交AB于Q ‎∴BP＝2EB ‎∵BE⊥DE ‎ ‎∴∠BED＝∠PED＝90°‎ ‎∵EP＝EB，DE＝DE ‎ ‎∴△BED≌△PED ‎∴‎ ‎∴‎ ‎∴AC∥PD ‎ ‎∴∠BQD＝∠A＝90° ‎ ‎∴‎ ‎∴∠PQB＝90°‎ 在△PQB 与△FQD中 ‎∵∠PQB＝∠FQD，∠PBQ＝∠FDQ，‎ ‎∴△PQB∽△FQD ‎ ‎∴‎ ‎∵BP＝2BE ‎ ‎∴‎ ‎∴‎ ‎3. （2011陕西，20,8分）一天，某校数学课外活动小组的同学们，带着皮尺去测量某河道因挖沙形成的“圆锥形坑”的深度，来评估这些深坑对河道的影响．如图是同学们选择（确保测量过程中无安全隐患）的测量对象，测量方案如下：‎ ‎①先测量出沙坑坑沿圆周的周长约为‎34.54米；‎ ‎②甲同学直立于沙坑坑沿圆周所在平面上，经过适当调整自己所处的位置，当他位于点B时，恰好他的视线经过沙坑坑沿圆周上的一点A看到坑底S（甲同学的视线起点C与点A、点S三点共线）．经测量：AB=‎1.2米，BC=‎1.6米．‎ ‎ 根据以上测量数据，求“圆锥形坑”的深度（圆锥的高）．（π取3.14，结果精确到‎0.1米）‎ ‎【解】取圆锥底面圆圆心O，连接OS、OA，则∠O=∠ABC=90°，OS∥BC，∴∠ACB=∠ASO.∴△SOA∽△CBA .∴. ∴ ‎ ‎∵,BC=1.6, AB=1.2, ∴.‎ ‎∴“圆锥形坑”的深度约为‎7.3米.‎ ‎4. （2011广东佛山，18，6）如图，D 是 △ABC的边AB上一点,连结CD.若AD= 2，BD = 4, ∠ACD =∠B 求AC的长.‎ ‎【答案】解：在△ABC和△ACD中，‎ ‎∵∠ACD=∠B，∠A=∠A，∴△ABC∽△ACD ‎∴=‎ 即AC²=AD×AB=AD×(AD+BD)=2×6=12‎ ‎∴AC=2 ‎5. （2011黑龙江省哈尔滨市，28，10分）已知：在△ABC中，BC=‎2AC, ∠DBC=∠ACB,BD=BC,CD交线段AB于点E。‎ ‎（1）如图1，当∠ACB=90°时，则线段DE、CE之间的数量关系为 。‎ ‎（2）如图2，当∠ACB=120°时，求证：DE=3CE;‎ ‎（3）如图3，在（2）的条件下，点F是BC边的中点，连接DF，DF与AB交于点G,△DKG和△DBG关于直线DG对称（点B的对称点是点K）,延长DK交AB于点H，若BH=10，求CE的长。‎ ‎【答案】解：（1）DE=2EC ‎（2）证明：如图1，∵∠DBC=∠ACB=120° DB=BC ‎∴∠D=∠BCD=30° ∴ ∠ACD=90°‎ 过点B作BM⊥DC于M 则DM=MC BM=BC ‎∵AC=BC ∴BM=AC 又∵∠BMC=∠ACM=90° ∠MEB=∠CEA ‎∴△BME≌△ACE ∴ME=CE=CM ∴DE=3EC ‎ ‎（3）如图2： 过点B作BM’ ⊥DC于M’，过点F作FN⊥DB交DB的延长线于点N,‎ ‎ 设BF=a ‎ ∵∠DBF=120° ∴∠FBN=60° ∴FN=a BN=a ‎∵DB=BC=2BF=‎2a ∴DN=DB+BN=a ‎∴DF=‎ ‎∵AC=BC BF=BC ∴BF=AC ‎∴△DBF≌△BCA ∴∠BDF=∠CBA 又∵∠BFG=∠DFB ∴△FBG∽△FDB ∴‎ ‎∴BF2=FG·FD ∴a2=a·FG ∴FG=‎ ‎∴DG=DF-FG= BG=‎ ‎∵△DKG和△DBG关于直线DG对称 ∴∠GDH=∠BDF ∴∠ABC=∠GDH 又∵∠BGF=∠DGH ∴△BGF∽△DGH ∴‎ ‎∴‎ ‎∵BH=BG+GH= ∴a=‎ ‎∴BC=‎2a= CM’=BC·cos30°=‎ ‎∴DC=‎2CM’=‎ ‎∵ DE=3EC ‎∴CE=‎ ‎ ‎