2011黄石市中考数学试题及答案 10页

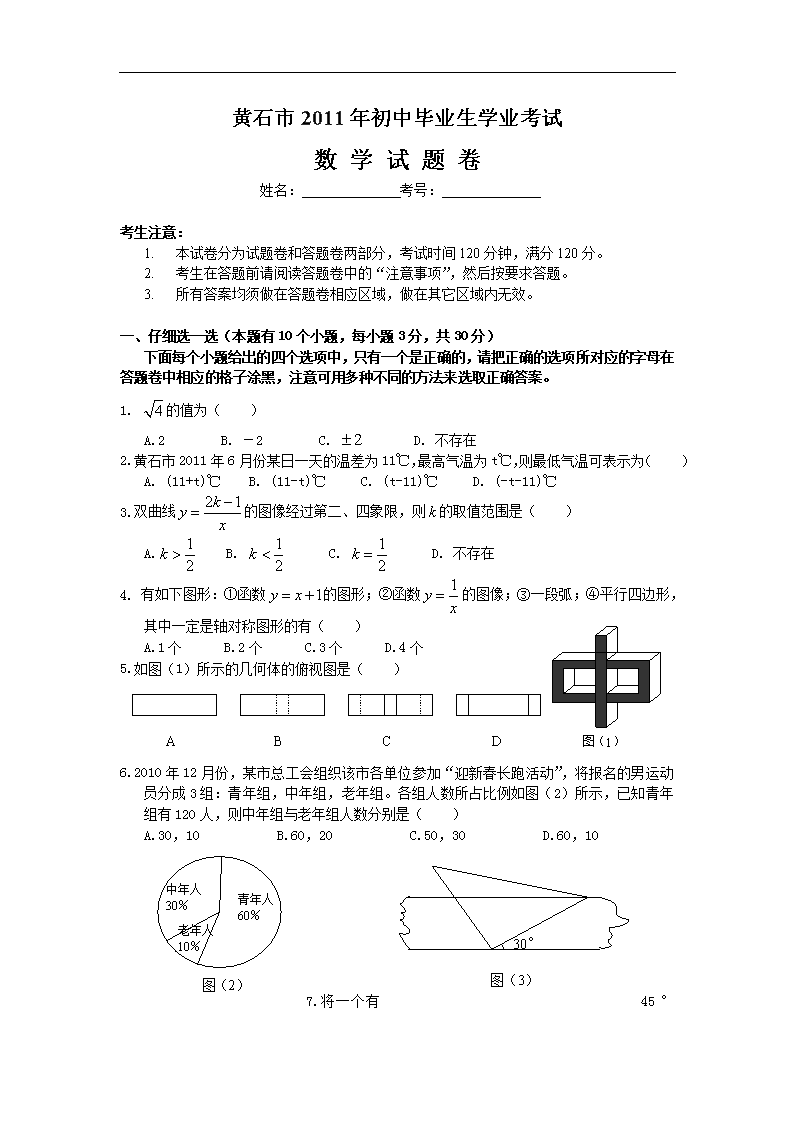
黄石市2011年初中毕业生学业考试 数 学 试 题 卷 姓名： 考号： ‎ 考生注意：‎ 1. 本试卷分为试题卷和答题卷两部分，考试时间120分钟，满分120分。‎ 2. 考生在答题前请阅读答题卷中的“注意事项”，然后按要求答题。‎ 3. 所有答案均须做在答题卷相应区域，做在其它区域内无效。‎ 一、仔细选一选（本题有10个小题，每小题3分，共30分）‎ 下面每个小题给出的四个选项中，只有一个是正确的，请把正确的选项所对应的字母在答题卷中相应的格子涂黑，注意可用多种不同的方法来选取正确答案。‎ ‎1. 的值为（ ）‎ A.2 B. －2 C. D. 不存在 ‎2.黄石市2011年6月份某日一天的温差为11℃，最高气温为t℃，则最低气温可表示为（ ）‎ A. (11+t)℃ B. (11-t)℃ C. (t-11)℃ D. (-t-11)℃‎ ‎3.双曲线的图像经过第二、四象限，则的取值范围是（ ）‎ A. B. C. D. 不存在 图（1）‎ ‎4. 有如下图形：①函数的图形；②函数的图像；③一段弧；④平行四边形，其中一定是轴对称图形的有（ ） ‎ A.1个 B.2个 C.3个 D.4个 A B C D ‎5.如图（1）所示的几何体的俯视图是（ ）‎ ‎6.2010年12月份，某市总工会组织该市各单位参加“迎新春长跑活动”，将报名的男运动员分成3组：青年组，中年组，老年组。各组人数所占比例如图（2）所示，已知青年组有120人，则中年组与老年组人数分别是（ ）‎ A.30，10 B.60，20 C.50，30 D.60，10‎ ‎30°‎ 图（3）‎ ‎ ‎ 中年人 ‎30％‎ 青年人 ‎60％‎ ‎ ‎ 老年人 ‎10％‎ 图（2）‎ ‎7.将一个有45°‎ 角的三角板的直角顶点放在一张宽为3cm的纸带边沿上，另一个顶点在纸带的另一边沿上，测得三角板的一边与纸带的一边所在的直线成30°角，如图（3），则三角板的最大边的长为（ ）‎ A. B. C. D. ‎ ‎8.平面上不重合的两点确定一条直线，不同三点最多可确定3条直线，若平面上不同的个点最多可确定21条直线，则的值为（ ）‎ A. B. C. D. ‎ ‎9.设一元二次方程的两根分别为，且，则满足（ ）‎ A. B. C. D. 且 ‎ ‎10.已知梯形的四个顶点的坐标分别为，，，，直线将梯形分成面积相等的两部分，则的值为（ ）‎ A. B. C. D. ‎ 二、认真填一填（本题有6个小题，每小题3分，共18分）‎ ‎11.分解因式：＝ .‎ ‎12.为响应“红歌唱响中国”活动，某乡镇举行了一场“红歌”歌咏比赛，组委会规定：任何一名参赛选手的成绩满足：，赛后整理所有参赛选手的成绩如表（一）‎ 分 数 段 频数 频率 ‎30‎ ‎0.15‎ ‎0.45‎ ‎60‎ ‎20‎ ‎0.1‎ ‎ 表（一）‎ 根据表（一）提供的信息得到 .‎ ‎13.有甲、乙两张纸条，甲纸条的宽是乙纸条宽的2倍，如图（4）。将这两张纸条交叉重叠地放在一起，重合部分为四边形，则与的数量关系为 .‎ ‎14.如图（5），△内接于⊙，若＝30°，，则⊙的直径为 .‎ B C A O 图（5）‎ 乙 甲 A D B C 图（4）‎ ‎15.若一次函数的图像与反比例函数的图像没有公共点，则实数的取值范围是 .‎ ‎16.初三年级某班有54名学生，所在教室有6行9列座位，用表示第行第列的座位，新学期准备调整座位，设某个学生原来的座位为，如果调整后的座位为，则称该生作了平移[],并称为该生的位置数。若某生的位置数为，则当取最小值时，的最大值为 .‎ 三、全面答一答（本题有9个小题，共72分）‎ 解答应写出文字说明，证明过程或推演步骤，如果觉得有的题目有点困难，那么把自己能写出的解答尽量写出来。‎ ‎17.（本小题满分7分）计算： ‎ ‎18.（本小题满分7分）先化简，再求值：，其中.‎ A B C D E 图（6）‎ ‎19.（本小题满分7分）如图（6），在等腰梯形中，，，是的中点，连接.、。‎ 求证：.‎ ‎20.（本小题满分8分）解方程： ‎ ‎21.（本小题满分8分）2011年6月4日，李娜获得法网公开赛的冠军，圆了中国人的网球梦，也在国内掀起一股网球热。某市准备为青少年举行一次网球知识讲座，小明和妹妹都是网球球迷，要求爸爸去买门票，但爸爸只买回一张门票，那么谁去就成了问题，小明想到一个办法：他拿出一个装有质地、大小相同的个红球与个白球的袋子，让爸爸摸出一个球，如果摸出的是红球，妹妹去听讲座，如果摸出的是白球，小明去听讲座。‎ ‎（1）爸爸说这个办法不公平，请你用概率的知识解释原因。‎ ‎（2）若爸爸从袋中取出个白球，再用小明提出的办法来确定谁去听讲座，请问摸球的结果是对小明有利还是对妹妹有利，说明理由。‎ 东方山 月亮山 图（7）‎ β α A B D C ‎22.（本小题满分8分）东方山是鄂东南地区的佛教圣地，月亮山是黄荆山脉第二高峰，山顶上有黄石电视塔。据黄石地理资料记载：东方山海拔453.20米，月亮山海拔442.00米，一飞机从东方山到月亮山方向水平飞行，在东方山山顶的正上方处测得月亮山山顶的俯角为，在月亮山山顶的正上方处测得东方山山顶处的俯角为，如图（7）。已知，若飞机的飞行速度为180米/秒，则该飞机从到处需多少时间？（精确到0.1秒）‎ ‎23.（本小题满分8分）今年，号称“千湖之省”的湖北正遭受大旱，为提高学生环境意识，节约用水，某校数学教师编制了一道应用题：‎ 为了保护水资源，某市制定一套节水的管理措施，其中对居民生活用水收费作如下规定：‎ 月用水量（吨）‎ 单价（元/吨）‎ 不大于10吨部分 ‎1.5‎ 大于10吨不大于吨部分()‎ ‎2‎ 大于吨部分 ‎3‎ ‎（1）若某用户六月份用水量为18吨，求其应缴纳的水费；‎ ‎（2）记该用户六月份用水量为吨，缴纳水费为元，试列出与的函数式；‎ ‎（3）若该用户六月份用水量为40吨，缴纳水费元的取值范围为，试求 的取值范围。‎ 各位同学，请你也认真做一做，相信聪明的你一定会顺利完成。‎ ‎24.（本小题满分9分）已知⊙与⊙相交于、两点，点在⊙上，为⊙上一点（不与，，重合），直线与⊙交于另一点。‎ ‎（1）如图（8），若是⊙的直径，求证：；‎ ‎（2）如图(9)，若是⊙外一点，求证：；‎ ‎（3）如图（10），若是⊙内一点，判断（2）中的结论是否成立。‎ ‎ ‎ ‎25.（本小题满分10分）已知二次函数 ‎（1）当时，函数值随的增大而减小，求的取值范围。‎ ‎（2）以抛物线的顶点为一个顶点作该抛物线的内接正三角形（，两点在抛物线上），请问：△的面积是与无关的定值吗？若是，请求出这个定值；若不是，请说明理由。‎ ‎（3）若抛物线与轴交点的横坐标均为整数，求整数的值。‎ x y ‎0‎ A 湖北省阳新县三溪中学YAM QQ709885341‎ 黄石市2011年初中毕业生学业考试 数学答案及评分标准 一、选择题（每小题3分，共30分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 A C B C C B D C D A 二、填空题（每小题3分，共18分）‎ ‎11． 12． 13． 14． 15． 16．‎ 三、解答题（9小题，共72分）‎ ‎17．(7分)解：原式 （4分）‎ ‎ （3分）‎ ‎18．（7分）解：原式 （2分）‎ ‎ （2分）‎ ‎ （2分）‎ ‎ 当时，原式的值为1。 （ 1分）‎ ‎19．证明：∵四边形是等腰梯形 ∴ （2分）‎ 又是的中点 ‎∴ （2分）‎ 又 ‎∴． （2分） ‎ ‎∴． （1分）‎ ‎20．(8分)解：由题意得： （2分）‎ ‎ 由方程（2）得：代人（1）式得 ‎ （1分）‎ ‎ 解得，或． （2分）‎ 代人得或 （2分）‎ ‎21．（8分）解：（1）∵红球有2x个，白球有3x个，‎ ‎∴(红球)， (白球)， （2分）‎ ‎∴(红球) (白球) ∴这个办法不公平 （1分）‎ ‎（2）取出3个白球后，红球有2x个，白球有（）个，‎ ‎∴(红球)，(白球)，为正整数 （1分）‎ ‎∴(红球) (白球) （1分）‎ ‎①当时，则(红球) (白球) ∴对小妹有利；‎ ‎②当时，则(红球) (白球) ∴对小妹、小明是公平的；‎ ‎③当时，则(红球) (白球) ∴对小明有利； （3分）‎ ‎22．（8分）解：在△中，，‎ 在△中, （2分）‎ ‎∴ （2分）‎ ‎∴ （2分）‎ 故到所需的时间为（秒） （1分）‎ 答：飞机从到处需44.4秒． （1分）‎ 东方山 月亮山 β α A B D C ‎23．（8分）解：（1）六月份应缴纳的水费为：（元） （3分）‎ ‎（2）当时，‎ 当时，‎ 当时，‎ ‎∴ （3分）‎ ‎（3）当时，元，满足条件，‎ 当时，，则 ‎ ∴‎ 综上得， （2分）‎ ‎24．（9分）证明：（1）如图（一），连接，‎ ‎∵为⊙的直径 ∴‎ ‎∴为⊙的直径 ∴在上 又，为的中点 ‎∴△是以为底边的等腰三角形 ‎∴ （3分）‎ ‎（2）如图（二），连接，并延长交⊙与点，连 ‎∵四边形内接于⊙ ∴‎ 又∵ ∴‎ ‎∴‎ 又为⊙的直径 ∴‎ ‎∴ （3分）‎ ‎（3）如图（三），连接，并延长交⊙与点，连 ‎∵ 又 ‎∴ ‎ ‎∴ 又 ‎∴ （3分）‎ ‎25．（10分）解：（1）∵‎ ‎∴由题意得， （3分）‎ ‎（2）根据抛物线和正三角形的对称性，可知轴，设抛物线的对称轴与交于点，则。设 ‎∴‎ 又 ‎ ‎ ‎∴ ∴‎ ‎∴，‎ ‎∴定值 （3分）‎ x y ‎0‎ A N B M ‎（3）令，即时，有 由题意，为完全平方数，令 即 ‎∵为整数， ∴的奇偶性相同 ‎∴或 解得或 综合得 （4分）‎