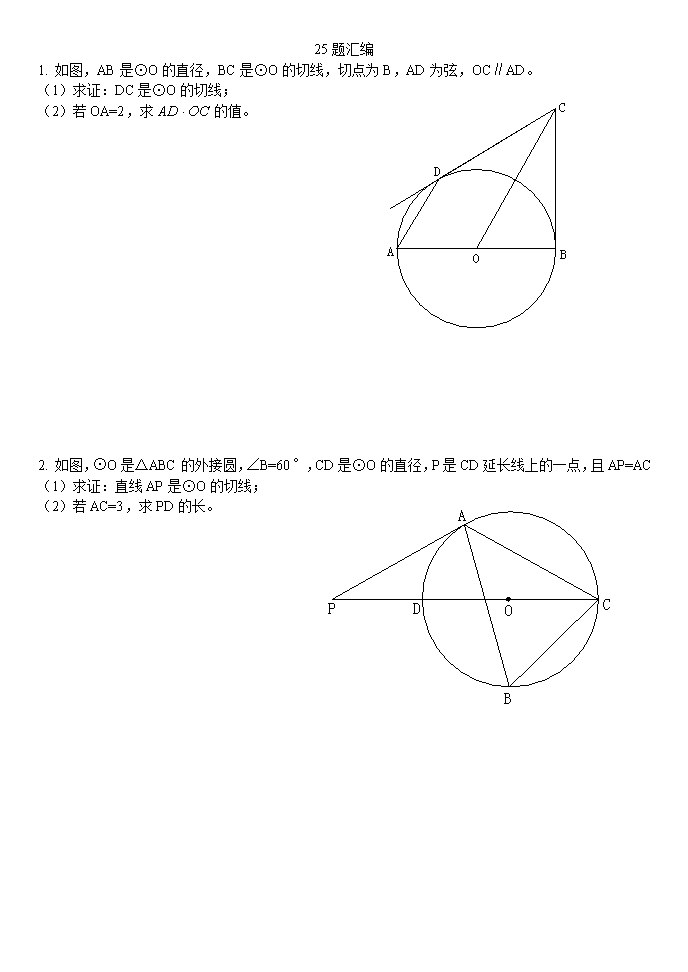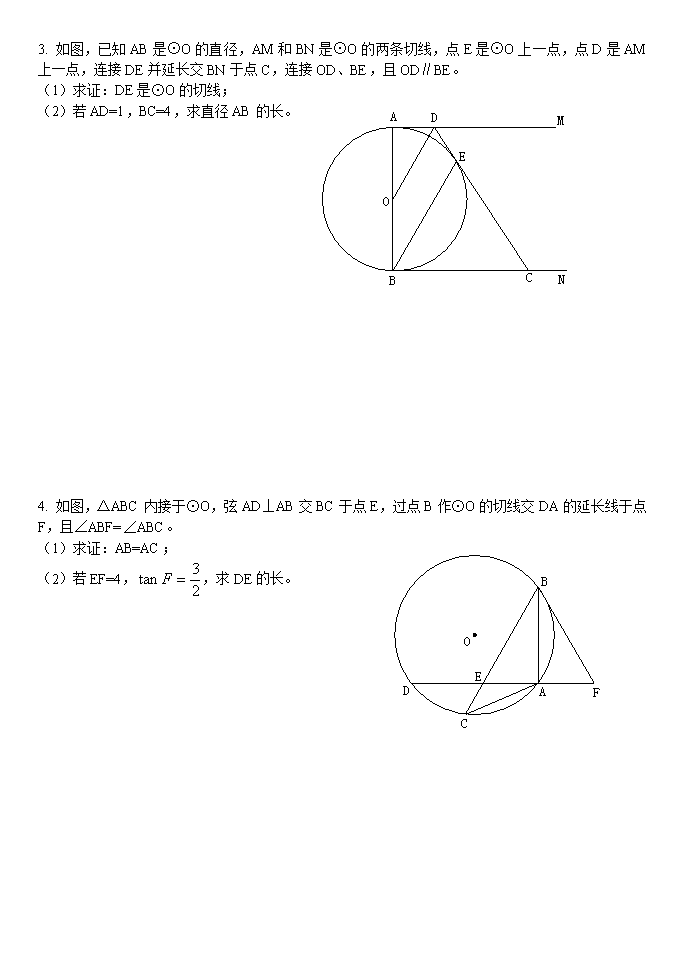中考数学圆综合题汇编 21页

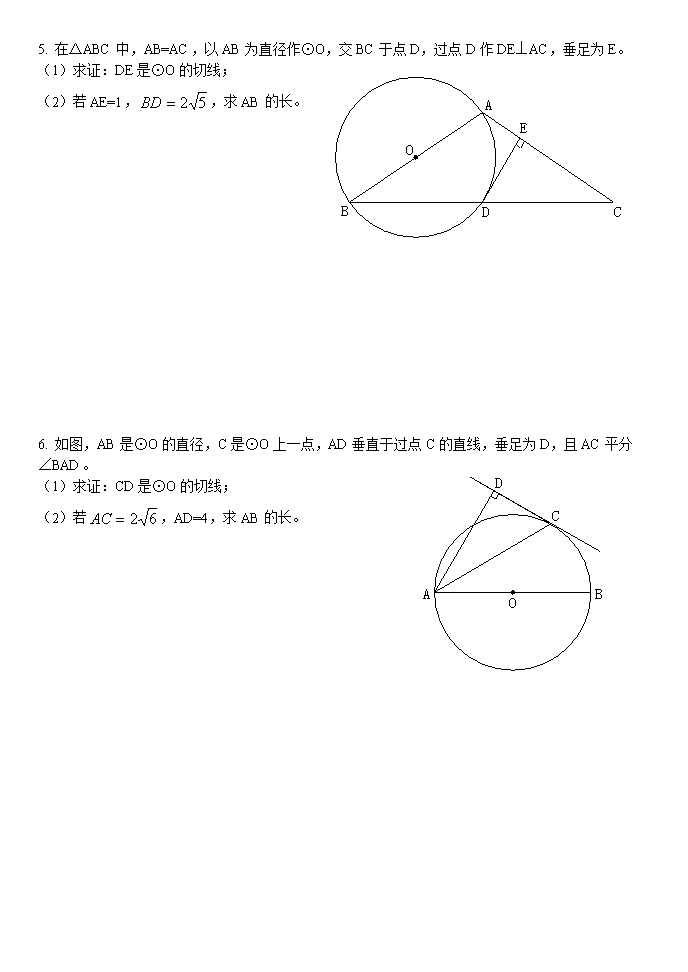
‎25题汇编 ‎1. 如图，AB是⊙O的直径，BC是⊙O的切线，切点为B，AD为弦，OC∥AD。‎ ‎（1）求证：DC是⊙O的切线；‎ ‎（2）若OA=2，求的值。‎ ‎2. 如图，⊙O是△ABC的外接圆，∠B=60°，CD是⊙O的直径，P是CD延长线上的一点，且AP=AC ‎（1）求证：直线AP是⊙O的切线；‎ ‎（2）若AC=3，求PD的长。‎ ‎3. 如图，已知AB是⊙O的直径，AM和BN是⊙O的两条切线，点E是⊙O上一点，点D是AM上一点，连接DE并延长交BN于点C，连接OD、BE，且OD∥BE。‎ ‎（1）求证：DE是⊙O的切线；‎ ‎（2）若AD=1，BC=4，求直径AB的长。‎ ‎4. 如图，△ABC内接于⊙O，弦AD⊥AB交BC于点E，过点B作⊙O的切线交DA的延长线于点F，且∠ABF=∠ABC。‎ ‎（1）求证：AB=AC；‎ ‎（2）若EF=4，，求DE的长。‎ ‎5. 在△ABC中，AB=AC，以AB为直径作⊙O，交BC于点D，过点D作DE⊥AC，垂足为E。‎ ‎（1）求证：DE是⊙O的切线；‎ ‎（2）若AE=1，，求AB的长。‎ ‎6. 如图，AB是⊙O的直径，C是⊙O上一点，AD垂直于过点C的直线，垂足为D，且AC平分 ‎∠BAD。‎ ‎（1）求证：CD是⊙O的切线；‎ ‎（2）若，AD=4，求AB的长。‎ ‎7. 如图，AB为⊙O的直径，C为⊙O上一点，AD和过C点的切线互相垂直，垂足为点D，AD交⊙O于点E。‎ 求证：（1）AC平分∠DAB；‎ ‎（2）若∠B=60°，，求AE的长。‎ ‎8. 如图，⊙O是△ABC的外接圆，AC是⊙O的直径，弦BD=BA，AB=12，BC=5，BE⊥DC交DC的延长线于点E。‎ ‎（1）求证：BE是⊙O的切线；‎ ‎（2）求DE的长。‎ ‎9. 如图，在Rt△ABC中，∠C=90°，CB=CA=6，半径为2的⊙F与射线BA相切于点G，且AG=4，将Rt△ABC绕点A顺时针旋转135°后得到Rt△ADE，点B、C的对应点分别是点D、E。‎ ‎（1）求证：DE为⊙F的切线；‎ ‎（2）求出Rt△ADE的斜边AD被⊙F截得的弦PQ的长度。‎ ‎10. ⊙O是等边三角形ABC的外接圆，点E在AB弧上，点D在AC弧上，且AE弧等于CD弧，连接CE交AB于点F，连接BD交CE于点H，交AC于点G，连接AD。‎ ‎（1）求证：AF=CG；‎ ‎（2）若，AC=8，求AD的长。‎ ‎11. 如图，⊙O是△ABC的外接圆，弦BD交AC于点E，连接CD，且AE=DE，BC=CE。‎ ‎（1）求∠ACB的度数；‎ ‎（2）过点O作OF⊥AC于点F，延长FO交BE于点G，DE=3，EG=2，求AB的长。‎ ‎12. 如图，在菱形ABCD中，P是对角线AC上的一点，且PA=PD，⊙O为△APD的外接圆。‎ ‎（1）求证：AB为⊙O的切线；‎ ‎（2）若⊙O的半径为，，求AC的长。‎ ‎13. 如图，AC弧等于BC弧，D、E分别是半径OA，OB的中点，CE的延长线交⊙O于点F。‎ ‎（1）求证：CD=CE；‎ ‎（2）若CD=2，CF=5，求半径OA的长。‎ ‎14. 如图，AB是⊙O的直径，点C在⊙O外，连接OC，OC⊥AB，弦BD交OC于点E，CD=CE。‎ ‎（1）求证：CD是⊙O的切线；‎ ‎（2）若AB=13，BD=12，求DE的长。‎ ‎15. 如图，点A在射线ON上，半径为5的⊙A与射线OM相切于点B，交射线ON于点D ‎（），将射线OM沿着射线ON翻折，得射线。‎ ‎（1）求证：为⊙A的切线；‎ ‎（2）点C在射线OM上，连CD，交⊙A于点E，若，，求弦DE的长。‎ ‎16. 如图，∠ABC=30°，半径为的⊙O与直线AB相切于点E，BE=1，将∠ABC沿着直线BC翻折，得到∠DBC。‎ ‎（1）求证：⊙O与BD相切；‎ ‎（2）点F与点E关于O点对称，过点F作GF∥BC，交射线BD于点G，求线段GF的长。‎ ‎17. 如图，在△ABC中，AB=10，BC=8，AC=6，将△ABC沿AC翻折，点B与D重合，O是CD上一点，OC=3，以O为圆心，OC为半径作⊙O，交CD于另一点E。‎ ‎（1）求证：直线AD是⊙O的切线；‎ ‎（2）过点D作⊙O的另一条切线，切点为点M，连接MC并延长，交AB边于点N，求线段MN的长。‎ ‎18. 如图，在⊙O中，弦AB∥弦CD，且AB、CD位于圆心O的两侧，AB=8，CD=6，AB、CD之间的距离为7，连接OA、OC。‎ ‎（1）求⊙O的半径；‎ ‎（2）过点A作⊙O的切线，交DC的延长线于点E，求线段CE的长。‎ ‎19. 如图，AB为⊙O的直径，AC、BC为⊙O的弦，，，将△ABC沿AC折叠，得到△ADC，点E在AD边上，AE=1，连接CE。‎ ‎（1）求证：CE是⊙O的切线；‎ ‎（2）作射线EO，交射线CB于点F，求BF的长。‎ ‎20.△如图，以△ABC的BC边上一点O为圆心的圆经过A,B两点，点D在⊙O上，BD=BA,∠DAC=2∠ABC,⊙O交BC于点E,AD交BC于点F。‎ ‎（1）求证：AC为⊙O的切线。‎ ‎（2）若AB=3,AC=,求BC长。‎ 答案：‎ ‎1.解：（1）连接OD ∵AB是⊙O的直径 ∴OA=OB=OD ∵BC是⊙O的切线，∴∠OBC=90°‎ ‎∵OC∥AD，∴∠A=∠COB，∠ODA=∠COD， ∵OA=OD，‎ ‎∴∠A=∠ODA ∴∠COD=∠COB ‎∵OC=OC，∴△COD≌△COB， ∴∠ODC=∠OBC=90°‎ ‎∴DC是⊙O的切线。‎ ‎（2）连接BD，∵AB是⊙O的直径，∴∠ADB=∠OBC=90°，‎ ‎∵∠BOC=∠A，∴△BAD∽△COB ‎∴ ∴ ∴OA=2，∴BA=2OA=4，OB=2 ∴ ‎ ‎2.（1）连接AO，则∠AOC=2∠B= ∵ OA=OC ∴∠OAC=∠OCA=‎ 又∵ PA=AC，∴∠P=∠ACP=30° 又∵∠AOP= ‎ ‎∴ ∴OA⊥AP ∴AP是⊙O的切线。‎ ‎（2）连AD，∵CD为直径，∴∠DAC=90°，∴ ∴‎ 又∵∠PAD= ∴∠P=∠PAD， ∴‎ ‎3. ‎ ‎（1）证明：连接OE，在⊙O中，OA=OE=OB，∴∠OBE=∠OEB，∵OD∥BE，‎ ‎∴∠AOD=∠OBE=∠OEB=∠EOD 又∵OA=OE，OD=OD，∴△AOD≌△EOD，∴∠OAD=∠OED ‎∵AM是⊙O的切线，切点为A，∴BA⊥AM，∴∠OAD=∠OED=90°，∴OE⊥DE ‎∵OE是⊙O的半径，∴DE是⊙O的切线。‎ ‎（2）解：过点D作BC的垂线，垂足为H。 ∵BN切⊙O于点B，∠ABC=90°=∠BAD=∠BHD ‎∴四边形ABHD是矩形，∴AD=BH=1， AB=DH ∴‎ ‎∵AD、CB、CD分别切⊙O于点A、B、E，∴AD=ED=1，BC=CE=4， ∴DC=DE+CE=1+4=5 ‎ 在Rt△DHC中，，∴‎ ‎4. （1）证明：连接BD，∵AD⊥AB，∴∠DAB=90°，∴BD为⊙O的直径，∵BF与⊙O切于点B，‎ ‎∴∠OBF=90°，∴∠OBA+∠BAF=90°，∵∠DAB=90°，∴∠D+∠DBA=90° ∴∠D=∠ABF ‎∵∠D=∠C，∠ABC=∠ABF，∴∠C=∠ABC ∴AB=AC ‎（2）∵AD⊥AB，∴∠AEB+∠ABE=∠ABF+∠F，∵∠ABF=∠ABC，∴∠BEF=∠F，∴BE=BF ‎∴AE=EF，∵EF=4，∴AF=2，∵∠BAF=90°，∴ AB=3 ∵∠DAB=∠BAF ‎∠ABF=∠D，∴△ABF∽△ADB ∴ ∴‎ ‎∵AE=2，∴‎ ‎5. （1）证明：连接OD、AD，∵AB为⊙O的直径，∴∠ADB=90°，又∵AB=AC，∴BD=DC 又∵OB=OA，∴OD∥AC ∴∠ODE=∠CED=90°，∴DE⊥OD ∴DE是⊙O的切线。‎ ‎（2）解：∵∠CED=∠CDA=90°，又∵∠C=∠C，∴△CED∽△CDA ∴‎ ‎∴ ∵ ，∴ ，∴CE=4‎ ‎∴AB=AC=5 ∴AB=5‎ ‎6. （1）证明：连接OC，∵OA=OC，∴∠1=∠2，∵AC平分∠BAD，∴∠1=∠3，∴∠2=∠3，‎ ‎∴OC∥AD ∴∠OCD=∠ADC， ∵AD⊥DC， ∴∠ADC=90°， ∴∠OCD=90°，‎ ‎∴CD是⊙O的切线 ‎（2）解：连接BC，∵AB是⊙O的直径，∴∠ACB=90°，又∵∠ADC=90°，∠1=∠3，‎ ‎∴cos∠1=cos∠3，即，∴ 把，AD=4代入得，得AB=6‎ ‎7. 证明：（1）如图1，连接OC，∵CD为⊙O的切线，∴OC⊥CD，∴∠OCD=90°，∵AD⊥CD，‎ ‎∴∠ADC=90°，∴∠OCD+∠ADC=180°，∴AD∥OC，∴∠1=∠2，∵OA=OC，∴∠2=∠3，‎ ‎∴∠1=∠3 即AC平分∠DAB ‎（2）如图2，∵AB为⊙O的直径，∴∠ACB=90°，又∵∠B=60°，∴∠1=∠3=30°，‎ 在Rt△ACD中，，∴，在Rt△ABC中，，‎ ‎∴，连接OE，∵∠EAO=2∠3=60°，OA=OE，‎ ‎∴△AOE是等边三角形，∴‎ ‎8. 解（1）连接OB、OD，在△ABO和△DBO中，，∴△ABO≌△DBO，∴∠DBO=∠ABO ‎∵∠ABO=∠OAB=∠BDC，∴∠DBO=∠BDC，∴OB∥ED，∵BE⊥DC，∴∠BEC=90°，‎ ‎∴∠EBO=90°，∴OB⊥BE，∴BE是⊙O的切线。‎ ‎（2）∵AC是⊙O的直径，∴∠ABC=90°，∵∠BDE=∠CAB，∠ABC=∠BED=90°，‎ ‎∴△BED∽△CBA，∴，∵BD=BA，AB=12，BC=5，∴‎ ‎∴，∴‎ ‎9. （1）证明：过F点作FM⊥DE于M，则∠FME=90°，CB=CA，∠C=90°，∴∠BAC=45°，‎ ‎∵∠CAE=135°，∴∠CAE+∠BAC=180°，∴点B、A、E在一条直线上，连接FG，‎ ‎∵⊙F与射线BA相切于点G，∴FG⊥AE，∴∠FGE=90°，又∵∠AED=90°，‎ ‎∴四边形FGEM为矩形，∴FM=GE，∵AE=AC=6，AG=4，∴GE=2，∴FM=2，∴ED是⊙F的切线。‎ ‎（2）解：∵FG=2，FG=GE，∴四边形FGEM为正方形，连接EF并延长交PQ于点N，∵四边形FGEM为正方形，∴EF平分∠AED，∵△ADE为等腰直角三角形，∴EN⊥PQ ∴PN=NQ，‎ ‎△AEN为等腰直角三角形，连接FP，由勾股定理得， 又∵AE=6， ∴ ‎ ‎∴，在Rt△PFN中，PF=2，由勾股定理得，∴‎ ‎10. （1）证明：∵弧AE等于弧CD，∴∠ACF=∠CBG，∵等边△ABC，∴AB=AC=BC，‎ ‎∠ABC=∠ACB=∠BAC=60°，∴△ACF≌△CBG，∴AF=CG。‎ ‎（2）过B作BK⊥AC，垂足为K，∵AC=8，∴AC=BC=8，∵，∴AF=CG=3，‎ AG=BF=5 ∵BK⊥AC ∴AK=CK=4 ，∴，∵在Rt△BCK中，‎ ‎，∴在Rt△BGK中，，∵∠D=∠BCG，‎ ‎∠BGC=∠AGD，∴△ADG∽△BGC，∴，，∴‎ ‎11. （1）证明：在⊙O中，∠A=∠D，∵∠AEB=∠DEC，AE=DE，∴△AEB≌△DEC，∴EB=EC，‎ 又∵BC=CE，∴BE=CE=BC，∴△EBC为等边三角形，∴∠ACB=60°。‎ ‎（2）解：∵OF⊥AC，∴AF=CF，∵△EBC为等边三角形，∴∠GEF=60°，∴∠EGF=30°，‎ ‎∵EG=2，∴EF=1，又∵AE=ED=3，∴CF=AF=4，∴AC=8，CE=5，∴BC=5，作BM⊥AC于点M，‎ ‎∵∠BCM=60°，∴∠MBC=30°，∴，‎ ‎∴， ∴‎ ‎12.（1）连接OA、OP、OD，设OP与AD交于点H，∵PA=PD，OA=OD，∴OP是线段AD的垂直平分线，∴OP⊥AD，∴∠AHP=90°，∵四边形ABCD是菱形，∴∠DAC=∠BAC，又∵OA=OP，‎ ‎∴∠OAP=∠OPA，∵在Rt△AHP中 ，∠DAP+∠OPA=90°，‎ ‎∴∠OAB=∠OAP+∠BAC=∠OPA+∠DAP=90°，即OA⊥AB，∵点A在⊙O上，∴直线AB与⊙O相切。‎ ‎（2）连接BD交AC于点E，则AC⊥BD。设⊙O的半径为r ，设AC=4a ，∴AE=2a ，‎ ‎∵ ，∴DE= a ，a ，a ，‎ 在Rt△AHP中，a ，（过程详细些，不能直接使用），在Rt△AHO中，由勾股定理得：，即，‎ 解得：（舍） ∴AC=8‎ ‎13. 证明：（1）连接CO，∵D、E分别是半径OA，OB的中点，又∵OA=OB，∴OD=OE，‎ ‎∵AC弧等于BC弧，∴∠AOC=∠BOC，∵OC=OC，∴△DOC≌△EOC，∴CD=CE。‎ ‎（2）延长BO交⊙O于点G，连接BC，GF，∵∠CBG与∠F为CG弧所对的圆周角，‎ ‎∴∠CBG=∠F，∵∠CEB=∠GEF，∴△CEB∽△GEF，∴，∵CE=CD=2，GE=3BE，‎ ‎∴ ，∴，∴，∴‎ ‎14.（1）连接OD，在⊙O中，OB=OD，∠B=∠ODB，∵CD=CE，∴∠CDE=∠CED，在△BEO中，‎ ‎∵OC⊥AB，∴∠BOE=90°，∴∠B+∠OEB=180°—90°=90°，∵∠CED=∠OEB，‎ ‎∴∠ODE+∠CDE=∠B+∠OEB=90°，∴OD⊥CD，∴CD是⊙O的切线。‎ ‎（2）连接AD，在△ABD中，∵AB是直径，∴∠ADB=90°=∠BOE，‎ ‎∵，∴，∴，∴ ‎ ‎15. .解：（1）连接AB，过A作AH⊥OM′,垂足为点H，‎ ‎∵⊙A与射线OM相切于点B，‎ ‎∴AB⊥OM 由翻折知，ON平分∠MOM′‎ ‎∴AH=AB ∴OM′为⊙A的切线 ‎（2）作CG⊥ON于点G，DF⊥OM于点F， ‎ AK⊥CD于点K，‎ ‎∵∠MO M′=90°，∴∠MON=45°‎ 设OF=a，则DF= a，‎ ‎∵tan∠OCD=，∴CF=‎7a，OD=a，‎ ‎∴OC=‎8a，∴OG=GC=a，∴DG=a，‎ ‎∴tan∠GDC==‎ 在Rt△ADK中，设DK=3b，则AK=4b，‎ 由勾股定理得，AD=5b，∴5b =5，∴b=1‎ ‎∴DE=2DK=6‎ ‎16..解：（1）连接OE，‎ ‎∵⊙O与直线AB相切于点E，‎ ‎∴OE⊥BH 连接OB，‎ ‎∵BE=1，OE=，∴tan∠EBO=‎ ‎∴∠EBO=60°‎ ‎∵∠ABC=30°，∴∠ABD=60°，‎ ‎∴∠OBD=60°，∴∠OBD=∠OBH=60°‎ 作ON⊥BD于点D，则ON=OE，‎ ‎∴BD与⊙O相切 ‎（2）连结OF，‎ ‎∵点F与点E关于O点中心对称，∴点E、O、F在一条直线上，‎ ‎∵GF∥BC，∴∠BGF=∠CBD=30°，‎ ‎∴∠EFG=360°-120°-90°-30°=120°，‎ 延长GF，交⊙O于另一点M，则∠OFM=60°‎ 连结OM，则OM=OF，∴△OFM为等边三角形，∴∠FOM=60°，‎ ‎∵∠NBE=∠NBO+∠FBO=120°，∴∠EON=60°，‎ ‎∴∠FOM+∠FON=∠EON+∠FON =180°，‎ 点M、O、N也在一条直线上 ‎∴MN=，∴GM=2MN=‎ ‎∵FM=OM=，∴GF=GM-FM=‎ ‎17. 解：（1）过O作OF⊥AD，垂足为F，‎ ‎∵AB=10，BC=8，AC=6，∴△ABC是直角三角形 ‎∴∠ACD=90º，‎ ‎∵∠OFD=90，∠D=∠D ‎∴△ACD∽△OFD.‎ ‎ ∵OC=3，∴OD=5，∴OF=3=OC ‎∴直线AD是⊙O的切线 ‎（2）连接ME,‎ ‎∵AB∥DM，∴△BNC≌△DMC， ‎ ‎∴CN=CM 由（1）可知DM=DF=4，DE=2，DC=8，‎ ‎∴DM2=DE·DC，‎ ‎∴△DEM∽△DMC. ‎ ‎∴-‎ 设EM=a，则CM=‎2a，EC=6，‎ 由勾股定理得CM=，∴MN=‎ ‎18.解：（1）过点O作OM⊥AB于点M，交CD于点N，‎ 则∠AMO=90°，AM=AB，‎ ‎∵AB∥CD，∴∠AMO+∠CNO=180°‎ ‎∴∠CNO=90°，∴CN=CD，‎ 设OM=x，则ON=7-x，‎ 由勾股定理得：AM2+MO2=AO2，CN2+NO2=CO2，‎ ‎∵AB=8，CD=6，∴AM=4，CN=3，‎ ‎∴16+ x2=9+(7-x)2，解得：x=3‎ ‎∴AO=5，‎ ‎（2）在△AOM与△OCN中，‎ ‎∵，，∠AMO=∠ONC=90°，‎ ‎∴△AOM∽△OCN，‎ ‎∴∠AOM=∠OCN，∠MAO=∠NOC，‎ ‎ ∴∠AOM+∠CON=90°，‎ ‎∴∠AOC=90°‎ ‎∵AE为⊙O的切线，∴∠OAE=90°，‎ ‎ ∴∠OAE+∠COA=180°，∴AE∥CO ‎ 延长CO，交AB于点F，则四边形AECF为平行四边形，‎ ‎∴CE=AF ‎ ∵∠AOM+∠FOM=∠OFM+∠FOM=90°，∴∠AOM=∠OFM ‎∵∠OAM=∠FAO， ∴△AOM∽△AFO，‎ ‎∴AO2=AM·AF，∴AF=，CE=‎ ‎19..解：（1）连接OC。∵△ADC是由△ABC折叠得到。‎ ‎∴∠ACD=90.∠CAD=CAB.AC=.‎ ‎∴AD=5. ∴‎ ‎∵∠CAD=∠CAD. ∴△ACE∽△ADC。‎ ‎∴∠ACD=∠AEC=90‎ ‎∴∠ACE+∠CAE=90. ∵OA=OC. ∴∠OAC=∠OCA ‎∵∠OAC=∠EAC.‎ ‎∴∠OCA+∠ECA=90. ∴CE为⊙O的切线 ‎（2）过B作BG∥OC，交OF于G。‎ ‎∵OA=OB, BG∥OC.‎ ‎∴△AOE≌△BOG.‎ ‎∴BG=AE, ‎ ‎∴△FBG∽△FOC. ‎ ‎∴.∴FB= ‎ ‎20.解：（1）连接AO ∵BD=AB ∴AB弧=BD弧 ∵弧BAE-弧AB=弧BDE-弧BD ∴弧AE=弧DE ‎∴∠ABF=∠DBF ∵AB=BD ∴∠AFO=90° ∵∠AOE=2∠ABC ∠DAC=2∠ABC ∴∠DAC=∠AOE ‎∵∠AOF+∠OAF=90° ∴∠OAF+∠FAC=90° ∴∠OAC=90° ∴AC是⊙O的切线 ‎（2）过点C作AB的垂线，交BA的延长线于点G，∵∠OAC=90°，∴∠OAB+∠CAG=90°‎ ‎∵∠CAG+∠GCA=90°，∴∠GCA=∠BAO，∵OA=OB，∴∠BAO=∠OBA，∴∠GCA=∠OBA ‎∵∠CGA=∠BGC，∴△CGA∽△BGC，∵，∴，设，‎ 在Rt△ACG内，，∴，∴‎ 解得或（舍去），∴，∴CG=2，∵CG=2，BG=4，∠BGC=90°，‎ ‎∴‎