中考直线与圆的位置关系知识点及提升练习 6页

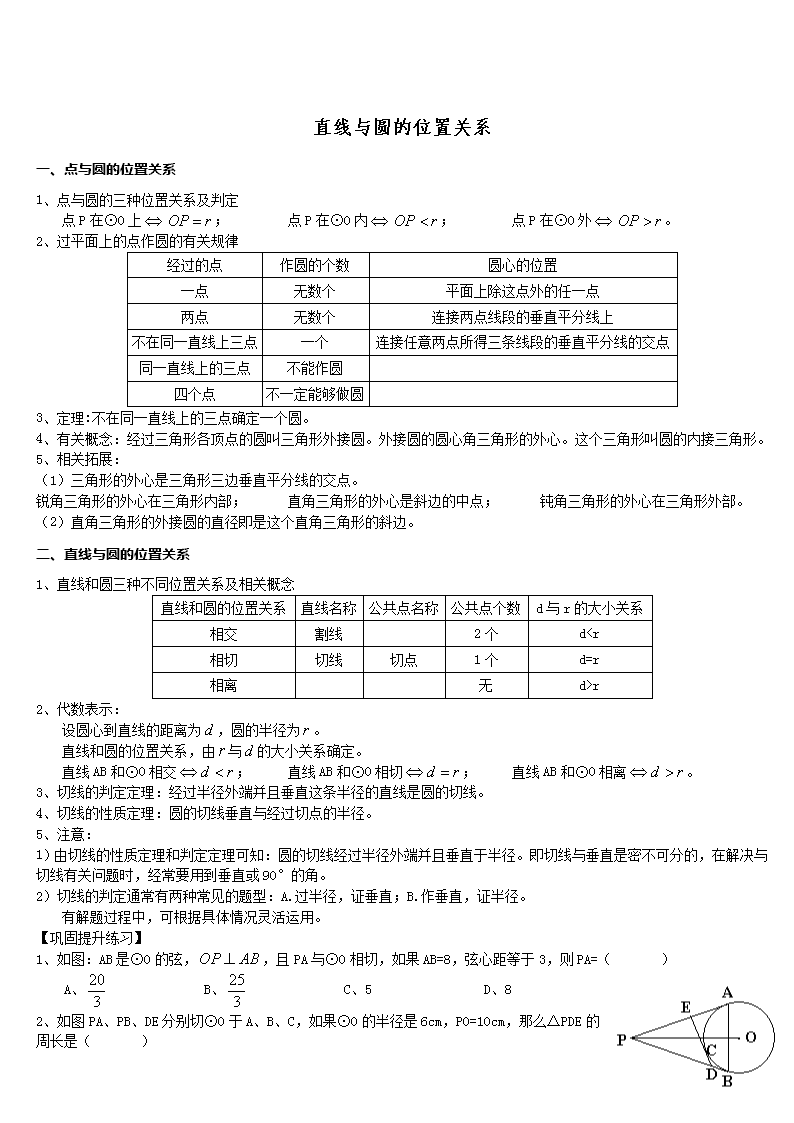
直线与圆的位置关系 一、点与圆的位置关系 ‎1、点与圆的三种位置关系及判定 ‎ 点P在⊙O上； 点P在⊙O内； 点P在⊙O外。 ‎ ‎2、过平面上的点作圆的有关规律 ‎ 经过的点 ‎ 作圆的个数 ‎ 圆心的位置 ‎ 一点 ‎ 无数个 ‎ 平面上除这点外的任一点 ‎ 两点 ‎ 无数个 ‎ 连接两点线段的垂直平分线上 ‎ 不在同一直线上三点 ‎ 一个 ‎ 连接任意两点所得三条线段的垂直平分线的交点 ‎ 同一直线上的三点 ‎ 不能作圆 ‎ ‎　 ‎ 四个点 ‎ 不一定能够做圆 ‎ ‎　 ‎ ‎3、定理:不在同一直线上的三点确定一个圆。‎ ‎4、有关概念：经过三角形各顶点的圆叫三角形外接圆。外接圆的圆心角三角形的外心。这个三角形叫圆的内接三角形。‎ ‎5、相关拓展：‎ ‎（1）三角形的外心是三角形三边垂直平分线的交点。 ‎ 锐角三角形的外心在三角形内部； 直角三角形的外心是斜边的中点； 钝角三角形的外心在三角形外部。‎ ‎（2）直角三角形的外接圆的直径即是这个直角三角形的斜边。 ‎ 二、直线与圆的位置关系 ‎1、直线和圆三种不同位置关系及相关概念 ‎ 直线和圆的位置关系 ‎ 直线名称 ‎ 公共点名称 ‎ 公共点个数 ‎ d与r的大小关系 ‎ 相交 ‎ 割线 ‎ ‎　 ‎ ‎2个 ‎ dr ‎ ‎2、代数表示： ‎ 设圆心到直线的距离为，圆的半径为。 ‎ 直线和圆的位置关系，由与的大小关系确定。 ‎ 直线AB和⊙O相交； 直线AB和⊙O相切； 直线AB和⊙O相离。 ‎ ‎3、切线的判定定理：经过半径外端并且垂直这条半径的直线是圆的切线。 ‎ ‎4、切线的性质定理：圆的切线垂直与经过切点的半径。 ‎ ‎5、注意：‎ ‎1）由切线的性质定理和判定定理可知：圆的切线经过半径外端并且垂直于半径。即切线与垂直是密不可分的，在解决与切线有关问题时，经常要用到垂直或90°的角。 ‎ ‎2）切线的判定通常有两种常见的题型：A.过半径，证垂直；B.作垂直，证半径。 ‎ 有解题过程中，可根据具体情况灵活运用。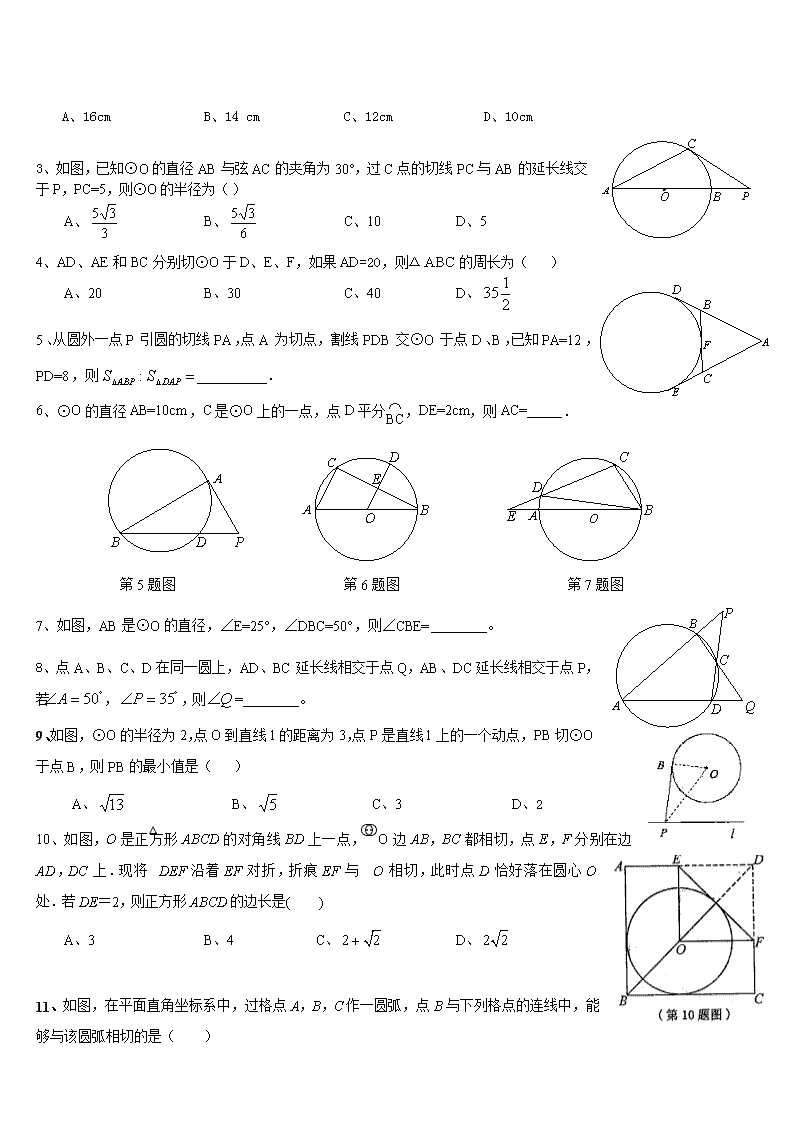 ‎ ‎【巩固提升练习】‎ ‎1、如图：AB是⊙O的弦，，且PA与⊙O相切，如果AB=8，弦心距等于3，则PA=（　　　 ） ‎ A、　　 B、　　 C、5　　 D、8 ‎ ‎2、如图PA、PB、DE分别切⊙O于A、B、C，如果⊙O的半径是‎6cm，PO=‎10cm，那么△PDE的周长是（　　　 ） ‎ A、16cm　　 B、14 cm　　 C、12cm　　 D、10cm ‎3、如图，已知⊙O的直径AB与弦AC的夹角为30°，过C点的切线PC与AB的延长线交于P，PC=5，则⊙O的半径为（ ）‎ A、 B、 C、10 D、5‎ ‎4、AD、AE和BC分别切⊙O于D、E、F，如果AD=20，则△的周长为（ ）‎ A、20 B、30 C、40 D、‎ ‎5、从圆外一点P引圆的切线PA，点A为切点，割线PDB交⊙O于点D、B，已知PA=12，PD=8，则__________．‎ ‎6、⊙O的直径AB=‎10cm，C是⊙O上的一点，点D平分，DE=‎2cm，则AC=_____．‎ ‎ 第5题图 第6题图 第7题图 ‎ ‎7、如图，AB是⊙O的直径，∠E=25°，∠DBC=50°，则∠CBE=________。‎ ‎8、点A、B、C、D在同一圆上，AD、BC延长线相交于点Q，AB、DC延长线相交于点P，若，，则=________。‎ ‎9、如图，⊙O的半径为2，点O到直线l的距离为3，点P是直线l上的一个动点，PB切⊙O于点B，则PB的最小值是（ ）‎ A、 B、 C、3 D、2‎ ‎10、如图，O是正方形ABCD的对角线BD上一点，⊙O边AB，BC都相切，点E，F分别在边AD，DC上．现将△DEF沿着EF对折，折痕EF与⊙O相切，此时点D恰好落在圆心O处．若DE＝2，则正方形ABCD的边长是( )‎ A、3 B、‎4 ‎ C、 D、‎ ‎11、如图，在平面直角坐标系中，过格点A，B，C作一圆弧，点B与下列格点的连线中，能够与该圆弧相切的是（ ）‎ C D A O P B ‎ 第12题图 A、点（0，3） B、点（2，3） C、点（5，1） D、点(6，1)‎ A B D O C ‎12、如图，AB为⊙O的直径，PD切⊙O于点C，交AB的延长线于D，且CO=CD，则（ ）‎ A．30° B．45° C．60° D．67.5°‎ ‎13、如图，AB是⊙O的直径，点D在AB的延长线上，DC切⊙O于点C，若，则等于 A．20° B．30° C．40° D．50°‎ O A B P E C ‎14、如图，AB为⊙O的直径，BC切⊙O于B，AC交⊙O于P，CE=BE，E在BC上. 求证：PE是⊙O的切线．‎ C D A O P B ‎ 第15题图 ‎15、如图，AB为⊙O的直径，PD切⊙O于点C，交AB的延长线于D，且CO=CD，则 A、30° B、45° C、60° D、‎ ‎16、如图，是的切线，切点为A，PA=2，，则的半径为（ ）‎ O P A A、1 B、 C、2 D、4‎ ‎17、已知于，，，，下列选项中⊙O的半径为的是 ‎18、如图，直线、与⊙O相切于点、，为⊙O上一点，且，则的度数是 ‎ ‎ A、70° B、105° C、100° D、110°‎ ‎19、如图，已知AB是⊙O的一条直径，延长AB至C点，使得，CD与⊙O相切，切点为D.若CD=，则线段BC的长度等于__________.‎ ‎ ‎ ‎20、如图，从⊙O外一点A引圆的切线AB，切点为B，连接AO并延长交圆于点C，连接BC．若，则的度数为 ．‎ ‎21、如图，已知直线交⊙O于A、B两点，AE是⊙O的直径,点C为⊙O上一点，且平分，过C作，垂足为D.‎ ‎(1) 求证：为⊙O的切线； (2) 若，⊙O的直径为10，求的长度.‎ ‎ ‎ ‎22、如图，AM为⊙O的切线，A为切点，于点D，BD交⊙O于C，OC平分.求的度数.‎ 三、三角形的外接圆 ‎（1）过三角形三个顶点的圆，叫做三角形的外接圆，三条边中垂线的交点，叫做三角形的外心。三角形的外心到各顶点的距离相等．‎ ‎（2）锐角三角形的外心在三角形内部，钝角三角形的外心在三角形的外部，直角三角形的外心在斜边中点，外接圆半径(为斜边长)．‎ 四、三角形的内切圆 ‎（1）到三角形三条边距离都相等的圆，叫三角形的内切圆，三角形中，三个内角平分线的交点，叫三角形的内心，三角形内心到三条边的距离相等，内心都在三角形的内部．‎ ‎（2）若三角形的面积为，周长为a+b+c,则内切圆半径为:，当为直角三角形的直角边，为斜边时，内切圆半径或.‎ 五、圆内接四边形的性质 ‎（1）圆内接四边形的对角互补； （2）圆内接四边形的任何一个外角等于它的对角．‎ 注意：①圆内接平行四边形为矩形；②圆内接梯形为等腰梯形．‎ 六、两个结论：‎ ‎·‎ I A BA CA ‎ 圆的外切四边形对边和相等； 圆的外切等腰梯形的中位线等于腰长．‎ ‎【巩固提升练习】‎ ‎1、如右图，I是的内心，则下列式子正确的是（ ）‎ A、∠BIC=-2∠A B、∠BIC=2∠A ‎ C、∠BIC=+∠A/2 D、∠BIC=-∠A/2‎ ‎2、直角三角形的两条直角边分别为5和12，那么它的外接圆的半径为 ，内切圆半径为 ．‎ ‎3、等边三角形内切圆半径，外接圆半径分别为，则= ．‎ ‎4、等边三角形的内切圆半径，外接圆半径的和高的比是 ．‎ ‎5、如果一个直角三角形的一条直角边等于它的外接圆的半径r，那么此三角形的面积与其外接圆的面积之比为（ ）‎ ‎ A． B． C． D．‎ ‎ 6、如图1，四边形ABCD内接于⊙O，若∠BOD=110°，则∠BCD=（ ）‎ A B C D O 图1‎ A B D C O 图2‎ A D P B C 图3‎ ‎ A．125° B．110° C．55° D．70°‎ ‎7、如图2，四边形ABCD内接于⊙O，∠ADC=60°，则∠ABC=（ ）‎ ‎︵‎ ‎ A．30° B．60° C．120° D．90°‎ ‎8、如图3，正方形ABCD内接于⊙O，点P在AD上，则∠BPC为（ ）‎ ‎ A．35° B．40° C．45° D．50°‎ ‎9、如图6，⊙I切△ABC于D、E、F，∠C=60°，∠EIF=100°，则∠B= 。‎ D A B C I ‎ E F 图6‎ A F C E B D O 图7‎ A D B C O 图8‎ ‎10、如图7，⊙O内切于Rt△ABC，∠C=90°，D、E、F为切点。若∠AOC=120°，则∠OAC= ，∠B= ；若AB=‎2cm，则AC= ,△ABC的外接圆半径= ，内切圆半径= 。‎ ‎11、如图8，若弦AD∥BC，∠BAC=70°，∠ABC=80°，则∠ADC= 度，∠ACD= 度。‎