中考数学考前辅导材料 7页

‎1、下列说法：‎ ‎①四边相等的四边形一定是菱形 ②顺次连接矩形各边中点形成的四边形一定是正方形 ‎③对角线相等的四边形一定是矩形 ④经过平行四边形对角线交点的直线，一定能把平行四边形分成面积相等的两部分 。其中正确的有（ ）个 A． B． C. D．‎ ‎2、如图，是⊙的直径，且经过弦的中点，已知，，则的长度为（ ）‎ A． B． C. D．‎ ‎3、如果三角形满足一个角是另一个角的3倍，那么我们称这个三角形为“智慧三角形”．下列各组数据中，能作为一个智慧三角形三边长的一组是（　　）‎ A．1，2，3 B．1，1， C．1，1， D．1，2，‎ ‎4、如图所示，抛物线的顶点为，与轴的交点在点和之间，以下结论：①；②；③；④其中正确的有（ ）个 A． B． C. 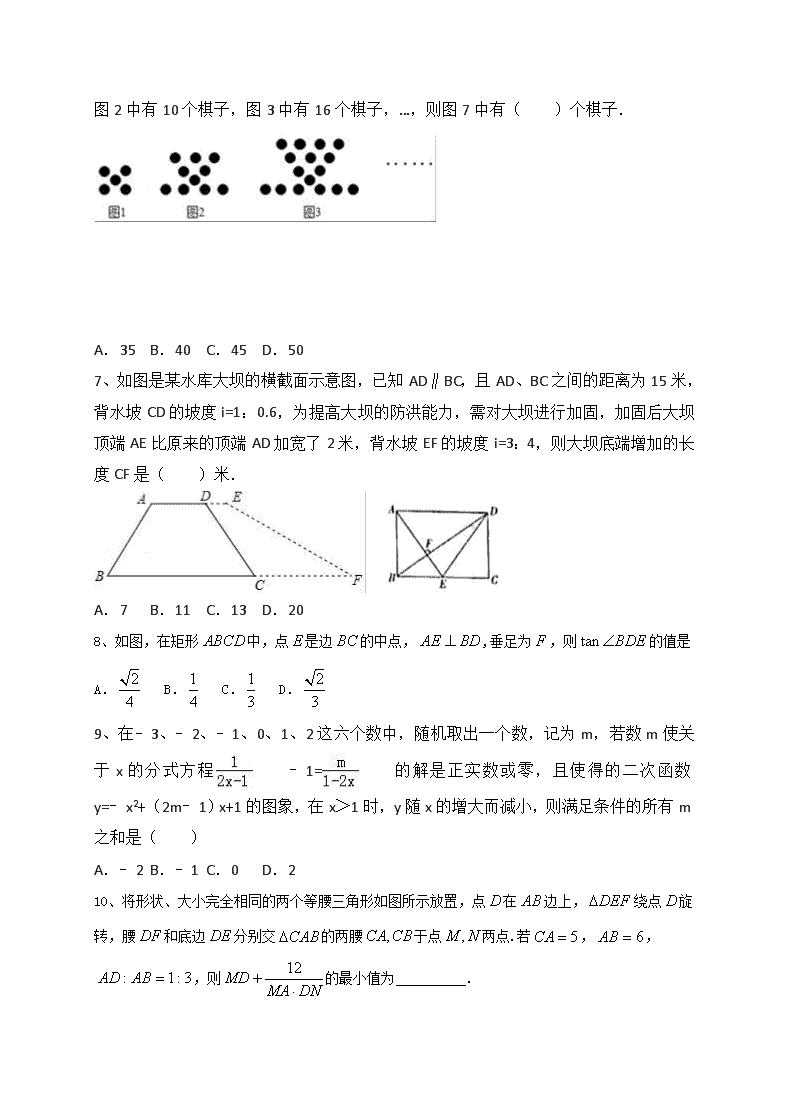D．‎ ‎5、如图，边长为2的等边△ABC和边长为1的等边△A′B′C′，它们的边B′C′，BC位于同一条直线l上，开始时，点C′与B重合，△ABC固定不动，然后把△A′B′C′自左向右沿直线l平移，移出△ABC外（点B′与C重合）停止，设△A′B′C′平移的距离为x，两个三角形重合部分的面积为y，则y关于x的函数图象是（　　）‎ A． B． C． D．‎ ‎6、下列图形是由同样大小的棋子按照一定规律排列而成的，其中，图1中有5个棋子，‎ 图2中有10个棋子，图3中有16个棋子，…，则图7中有（　　）个棋子．‎ A．35 B．40 C．45 D．50‎ ‎7、如图是某水库大坝的横截面示意图，已知AD∥BC，且AD、BC之间的距离为15米，背水坡CD的坡度i=1：0.6，为提高大坝的防洪能力，需对大坝进行加固，加固后大坝顶端AE比原来的顶端AD加宽了2米，背水坡EF的坡度i=3：4，则大坝底端增加的长度CF是（　　）米．‎ A．7 B．11 C．13 D．20‎ ‎8、如图，在矩形中，点是边的中点，,垂足为，则的值是 ‎ A． B． C． D．‎ ‎9、在﹣3、﹣2、﹣1、0、1、2这六个数中，随机取出一个数，记为m，若数m使关于x的分式方程﹣1=的解是正实数或零，且使得的二次函数y=﹣x2+（2m﹣1）x+1的图象，在x＞1时，y随x的增大而减小，则满足条件的所有m之和是（　　）‎ A．﹣2 B．﹣1 C．0 D．2‎ ‎10、将形状、大小完全相同的两个等腰三角形如图所示放置，点在边上，绕点旋转，腰和底边分别交的两腰于点两点.若，，，则的最小值为 ．‎ ‎1、从﹣1，﹣2，，四个数中，任取一个数记为k，再从余下的三个数中，任取一个数记为b．则一次函数y=kx+b的图象不经过第四象限的概率是　 　．‎ ‎2、同时抛掷两枚质地均匀的骰子，则事件“两枚骰子的点数和小于8且为偶数”的概率是 ．‎ ‎3、关于的分式方程的解为正实数，则实数的取值范围是 ．‎ ‎4、在中，已知和分别是边上的中线，且，垂足为，‎ 若，则线段的长为 ．‎ ‎5、在平面直角坐标系中，对于不在坐标轴上的任意一点，我们把点称为点的 “倒影点”．直线上有两点，它们的倒影点均在反比例函数的图像上．若，则____________．‎ ‎6、如图，在Rt△ABC中，∠ACB=90°，AC=BC=1．将Rt△ABC绕A点逆时针旋转30°后得到Rt△ADE，点B经过的路径为，则图中阴影部分的面积是 A. B. C. D. ‎ ‎7、如图1，把一张正方形纸片对折得到长方形，再沿的平分线折叠，如图2，点落在点处，最后按图3所示方式折叠，使点落在的中点处，折痕是．若原正方形纸片的边长为，则_____________．‎ ‎8、甲、乙两人在1800米长的直线道路上跑步，甲、乙两人同起点、同方向出发，并分别以不同的速度匀速前进．已知，甲出发30秒后，乙出发，乙到终点后立即返回，并以原来的速度前进，最后与甲相遇，此时跑步结束．如图，y（米）表示甲、乙两人之间的距离，t（秒）表示甲出发的时间，图中折线及数据表示整个跑步过程中y与t函数关系．那么，乙到终点后　 　秒与甲相遇．‎ ‎1、我市“尚品”房地产开发公司预计今年10月份将竣工一商品房小区，其中包括高层住宅区和别墅区一共60万平方米，且高层住宅区的面积不少于别墅区面积的3倍．‎ ‎（1）别墅区最多多少万平方米？‎ ‎（2）今年一月初，“尚品”公司开始出售该小区，其中高层住宅区的销售单价为8000元/平方米，别墅区的销售单价为12000元/平方米，并售出高层住宅区6万平方米，别墅区4万平方米，二月时，受最新政策“去库存，满足刚需”以及银行房贷利率打折的影响，该小区高层住宅区的销售单价比一月增加了a%，销售面积比一月增加了2a%；别墅区的销售单价比一月份减少了10%，销售面积比一月增加了a%，于是二月份该小区高层住宅区的销售总额比别墅区的销售总额多10080万元，求a的值．‎ ‎2、如图，AB为⊙O的直径，C为⊙O上一点，过点C作⊙O的切线，交BA的延长线交于点D，过点B作BE⊥BA，交DC延长线于点E，连接OE，交⊙O于点F，交BC于点H，连接AC．‎ ‎（1）求证：∠ECB=∠EBC；‎ ‎（2）连接BF，CF，若CF=6，sin∠FCB=，求AC的长．‎ ‎3、  某公司准备购进一批产品进行销售，该产品的进货单价为6元/个．根据市场调查，得到了四组关于日销售量y(个)与销售单价x(元/个)的数据，如表 (1)如果在一次函数、二次函数和反比例函数这三个函数模型中，选择一个来描述日销售量与销售单价之间的关系，你觉得哪个合适？并写出y与x之间的函数关系式(不要求写出自变量的取值范围) (2)按照(1)中的销售规律，请你推断，当销售单价定为17.5元/‎ 个时，日销售量为多少？此时，获得日销售利润是多少？ (3)为了防范风险，该公司将日进货成本控制在900元(含900元)以内，按照(1)中的销售规律，要想获得的日销售利润最大，那么销售单价应定为多少？并求出此时的最大利润．‎ ‎4、如图，在中，为锐角，点为射线上一动点，连接，以为一 边且在的右侧作正方形．‎ 解答下列问题：‎ ‎（）如果，‎ ‎①当点在线段上时（与点不重合），如图，线段、之间的位置关系为__________，‎ 数量关系为__________．‎ ‎ ②当点在线段的延长线上时，如图，①中的结论是否仍然成立，为什么？‎ ‎（）如图，如果，，点在线段上运动．且，，，‎ 正方形的边与线段相交于点，求线段长的最大值．‎ ‎ ‎ ‎5、已知抛物线经过点和．‎ ‎（）求抛物线的解析式，并写出其顶点的坐标．‎ ‎（）如图，把抛物线沿着直线方向平移到某处时得到抛物线，此时点，分别平移到点，处．设点在抛物线上且在轴的上方，若是以为底的等腰直角三角形，‎ 求点的坐标．‎ ‎（）如图，在（）的条件下，设点是线段上一动点，交直线于点，点为线段的中点，当点从点向点运动时：①的值如何变化？请说明理由；②点到达点时，直接写出点经过的路线长．‎ ‎ ‎ ‎25．（分）如图，抛物线与轴交与，两点（点在点的右侧），与轴交于 点，连接，以为一边，点为对称中心作菱形，点是轴上的一个动点，设点 的坐标为，过点作轴的垂线交抛物线于点．‎ ‎ ‎ ‎（）求点，，的坐标．‎ ‎（）当点在线段上运动时，直线分别交，于点，．试探究为何值时，四边形是平行四边形，此时，请判断四边形的形状，并说明理由．‎ ‎（）当点在线段上运动时，是否存在点，使为直角三角形？若存在，请直接写出点 的坐标；若不存在，请说明理由．‎ ‎22.（11分）定义：点P是△ABC内部或边上的点（顶点除外），在△PAB，△PBC，△PCA中，若至少有一个三角形与△ABC相似，则称点P是△ABC的自相似点．‎ 例如：如图1，点P在△ABC的内部，∠PBC=∠A，∠PCB=∠ABC，则△BCP∽△ABC，故点P为△ABC的自相似点．‎ 请你运用所学知识，结合上述材料，解决下列问题：‎ 在平面直角坐标系中，点M是曲线C：‎ 上的任意一点，点N是x轴正半轴上的任意一点．‎ （1） 如图2，点P是OM上一点，∠ONP=∠M, 试说明点P是△MON的自相似点； 当点M的坐标是，点N的坐标是时，求点P 的坐标；‎ ‎ ‎ ‎ 如图3，当点M的坐标是，点N的坐标是时，求△MON的自相似点的坐标；‎ （2） 是否存在点M和点N,使△MON无自相似点,？若存在，请直接写出这两点的坐标；若不存在，请说明理由．‎