宁波市2010年初三毕业生学业考试（含答案） 7页

宁波市2010年初三毕业生学业考试 数 学 试 题 一、选择题（每小题3分，共36分，在每小题给出的四个选项中，只有一项符合题目要求）‎ ‎1、－3的相反数是（ ）‎ ‎ A、3 B、 C、－3 D、‎ ‎2、下列运算正确的是（ ）‎ ‎ A、 B、 C、 D、‎ ‎3、下列各图是选自历届世博会徽中的图案，其中是中心对称图形的是（ ）‎ ‎ ‎ ‎ A、 B、 C、 D、‎ ‎4、据《中国经济周刊》报道，上海世博会第四轮环保活动投资总金额高达820亿元，其中820亿用科学记数法表示为（ ）‎ ‎ A、 B、 C、 D、‎ ‎5、《几何原本》的诞生，标志着几何学已成为一个有着严密理论系统和科学方法的学科，它奠定了现代数学的基础，它是下列哪位数学家的著作（ ）‎ ‎ A、欧几里得 B、杨辉 C、费马 D、刘徽 A C B E D O ‎（第8题）‎ ‎6、两圆的半径分别为3和5，圆心距为7，则两圆的位置关系是（ ）‎ ‎ A、内切 B、相交 C、外切 D、外离 ‎7、从1－9这九年自然数中任取一个，是2的倍数的概率是（ ）‎ ‎ A、 B、 C、 D、‎ ‎8、如图，直线AB与直线CD相交于点O，E是内一点，已知 OE⊥AB，，则的度数是（ ）‎ ‎ A、 B、 C、 D、‎ ‎9、为了参加市中学生篮球运动会，一支校篮球队准备购买10双运动鞋，各种尺码统计如下表： ‎ 尺码（厘米）‎ ‎25‎ ‎25.5‎ ‎26‎ ‎26.5‎ A B C D E ‎（第10题）‎ ‎27‎ 购买量（双）‎ ‎1‎ ‎2‎ ‎3‎ ‎2‎ ‎2‎ ‎ 则这10双运动鞋尺码的众数和中位数分别为（ ）‎ ‎ A、25.5厘米，26厘米 B、26厘米，25.5厘米 C、25.5厘米，25.5厘米 D、26厘米，26厘米 ‎10、如图，在△ABC中，，，BD、CE分别是 ‎△ABC、△BCD的角平分线，则图中的等腰三角形有（ ）‎ ‎ A、5个 B、4个 C、3个 D、2个 ‎11、已知反比例函数，下列结论不正确的是（ ）‎ ‎ A、图象经过点（1，1） B、图象在第一、三象限 C、当时， D、当时，随着的增大而增大 ‎12、骰子是一种特的数字立方体（见图），它符合规则：相对两面的点数之和总是7，下面四幅图中可以折成符合规则的骰子的是（ ）‎ ‎ A、 B、 C、 D、‎ 二、填空题（每小题3分，共18分）‎ ‎13、实数4的算术平方根是_________。‎ ‎14、请你写出一个满足不等式的正整数的值：____________。‎ ‎15、如图，某河道要建造一座公路桥，要求桥面离地面高度AC为‎3米，引桥的坡角为，则引桥的水平距离BC的长是_________米（精确到‎0.1米）。‎ ‎16、如图，在等腰梯形ABCD中，AD∥BC，，若，，则梯形ABCD的周长为____________。‎ ‎17、若，，则___________。‎ x O P y ‎18、如图，已知⊙P的半径为2，圆心P在抛物线上运动，当⊙P与轴相切时，圆心P的坐标为___________。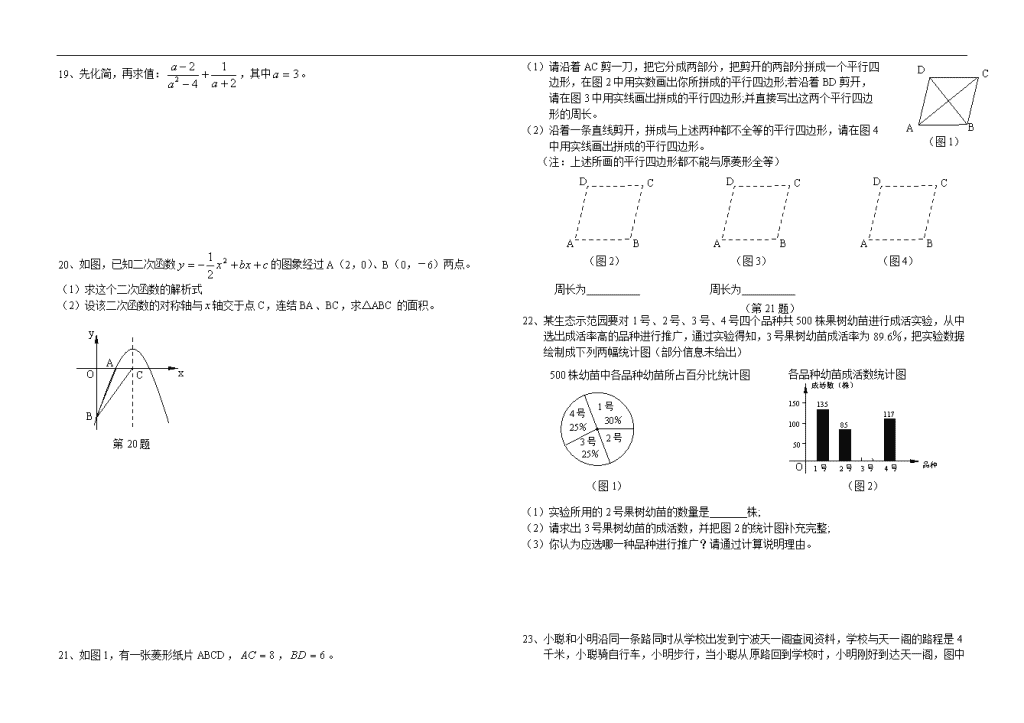‎ A B C D A B C 第18题 第16题 第15题 三、解答题（第19－21题各6分，第22题9分，第23题8分，第24题9分，第25题10分，第26题12分，共66分）‎ ‎19、先化简，再求值：，其中。‎ ‎20、如图，已知二次函数的图象经过A（2，0）、B（0，－6）两点。‎ ‎（1）求这个二次函数的解析式 ‎（2）设该二次函数的对称轴与轴交于点C，连结BA、BC，求△ABC的面积。‎ y x C A O B 第20题 ‎21、如图1，有一张菱形纸片ABCD，，。‎ D A B C ‎（1）请沿着AC剪一刀，把它分成两部分，把剪开的两部分拼成一个平行四 边形，在图2中用实数画出你所拼成的平行四边形;若沿着BD剪开，‎ 请在图3中用实线画出拼成的平行四边形;并直接写出这两个平行四边 形的周长。‎ ‎（图1）‎ ‎（2）沿着一条直线剪开，拼成与上述两种都不全等的平行四边形，请在图4‎ 中用实线画出拼成的平行四边形。‎ ‎（注：上述所画的平行四边形都不能与原菱形全等）‎ D A B C D A B C D A B C ‎（图4）‎ ‎（图3）‎ ‎（图2）‎ ‎ 周长为__________ 周长为__________‎ ‎（第21题）‎ ‎22、某生态示范园要对1号、2号、3号、4号四个品种共500株果树幼苗进行成活实验，从中选出成活率高的品种进行推广，通过实验得知，3号果树幼苗成活率为89.6％，把实验数据绘制成下列两幅统计图（部分信息未给出）‎ ‎4号 ‎25％‎ ‎30％‎ ‎1号 ‎3号 ‎25％‎ ‎2号 ‎（图1）‎ ‎500株幼苗中各品种幼苗所占百分比统计图 成活数（株）‎ 品种 O ‎1号 ‎2号 ‎3号 ‎4号 ‎135‎ ‎85‎ ‎117‎ ‎50‎ ‎100‎ ‎150‎ ‎（图2）‎ 各品种幼苗成活数统计图 ‎（1）实验所用的2号果树幼苗的数量是_______株;‎ ‎（2）请求出3号果树幼苗的成活数，并把图2的统计图补充完整;‎ ‎（3）你认为应选哪一种品种进行推广？请通过计算说明理由。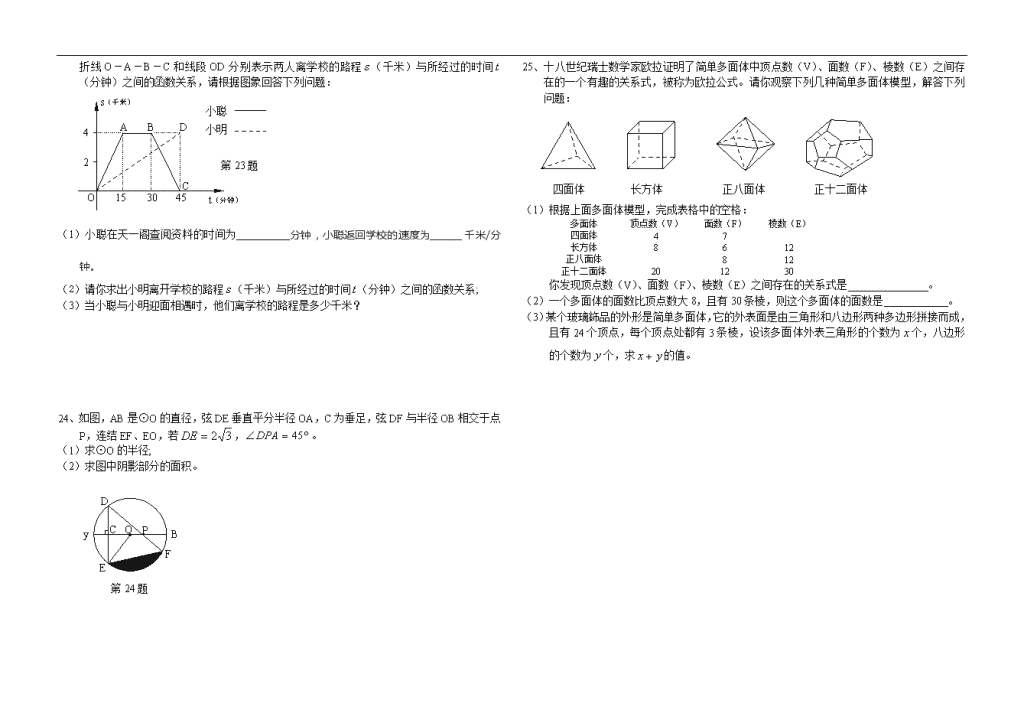‎ ‎23、小聪和小明沿同一条路同时从学校出发到宁波天一阁查阅资料，学校与天一阁的路程是‎4千米 ‎，小聪骑自行车，小明步行，当小聪从原路回到学校时，小明刚好到达天一阁，图中折线O－A－B－C和线段OD分别表示两人离学校的路程（千米）与所经过的时间（分钟）之间的函数关系，请根据图象回答下列问题：‎ s（千米）‎ t（分钟）‎ A B D C ‎30‎ ‎45‎ ‎15‎ O ‎2‎ ‎4‎ 小聪 小明 第23题 ‎（1）小聪在天一阁查阅资料的时间为__________分钟，小聪返回学校的速度为_______千米/分钟。‎ ‎（2）请你求出小明离开学校的路程（千米）与所经过的时间（分钟）之间的函数关系;‎ ‎（3）当小聪与小明迎面相遇时，他们离学校的路程是多少千米？‎ ‎24、如图，AB是⊙O的直径，弦DE垂直平分半径OA，C为垂足，弦DF与半径OB相交于点P，连结EF、EO，若，。‎ ‎（1）求⊙O的半径;‎ ‎（2）求图中阴影部分的面积。‎ y C O P B F E D 第24题 ‎25、十八世纪瑞士数学家欧拉证明了简单多面体中顶点数（V）、面数（F）、棱数（E）之间存在的一个有趣的关系式，被称为欧拉公式。请你观察下列几种简单多面体模型，解答下列问题：‎ 正十二面体 正八面体 长方体 四面体 ‎（1）根据上面多面体模型，完成表格中的空格：‎ 多面体 顶点数（V）‎ 面数（F）‎ 棱数（E）‎ 四面体 ‎4‎ ‎7‎ 长方体 ‎8‎ ‎6‎ ‎12‎ 正八面体 ‎8‎ ‎12‎ 正十二面体 ‎20‎ ‎12‎ ‎30‎ 你发现顶点数（V）、面数（F）、棱数（E）之间存在的关系式是_______________。‎ ‎（2）一个多面体的面数比顶点数大8，且有30条棱，则这个多面体的面数是____________。‎ ‎（3）某个玻璃鉓品的外形是简单多面体，它的外表面是由三角形和八边形两种多边形拼接而成，且有24个顶点，每个顶点处都有3条棱，设该多面体外表三角形的个数为个，八边形的个数为个，求的值。‎ ‎26、如图1、在平面直角坐标系中，O是坐标原点，□ABCD的顶点A的坐标为（－2，0），点D的坐标为（0，），点B在轴的正半轴上，点E为线段AD的中点，过点E的直线与轴交于点F，与射线DC交于点G。‎ ‎（1）求的度数;‎ ‎（2）连结OE，以OE所在直线为对称轴，△OEF经轴对称变换后得到△，记直线与射线DC的交点为H。‎ ‎①如图2，当点G在点H的左侧时，求证：△DEG∽△DHE;‎ y x C D A O B E G F ‎（图1）‎ x C D A O B E G H F y ‎（图2）‎ x C D A O B E y ‎（图3）‎ ‎②若△EHG的面积为，请直接写出点F的坐标。‎ 宁波市2010年初中毕业生学业考试 数学试题参考答案及评分标准 一、选择题 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 A C C B A B B B D A D C 二、填空题 题号 ‎13‎ ‎14‎ ‎15‎ ‎16‎ ‎17‎ ‎18‎ 答案 ‎2‎ ‎1，2，3中填一个即可 ‎11.2‎ ‎30‎ ‎7‎ ‎（（，2）或（，2）（对珍一个得2分）‎ 三、解答题（共66分）‎ ‎19、解：原式 ‎ ‎ 当时，原式 ‎20、解：（1）把A（2，0）、B（0，－6）代入 得：‎ 解得 ‎∴这个二次函数的解析式为 ‎（2）∵该抛物线对称轴为直线 ‎∴点C的坐标为（4，0）‎ ‎∴‎ ‎∴‎ ‎21、解：（1）‎ D A B C 周长为26‎ D A B C 周长为22‎ D A B C 答案不唯一 ‎22、解：（1）100‎ 成活数（株）‎ 品种 O ‎1号 ‎2号 ‎3号 ‎4号 ‎135‎ ‎85‎ ‎117‎ ‎50‎ ‎100‎ ‎150‎ ‎（图2）‎ 各品种幼苗成活数统计图 ‎117‎ ‎（2）‎ ‎（3）1号果树幼苗成活率为 ‎ 2号果树幼苗成活率为 ‎ 4号果树幼苗成活率为 ‎ ∵‎ ‎ ∴应选择4号品种进推广。‎ ‎23、解：（1）15，‎ ‎ （2）由图像可知，是的正比例函数 ‎ 设所求函数的解析式为（）‎ ‎ 代入（45，4）得：‎ ‎ 解得：‎ ‎ ∴与的函数关系式（）‎ ‎ （3）由图像可知，小聪在的时段内 ‎ 是的一次函数，设函数解析式为（）‎ ‎ 代入（30，4），（45，0）得：‎ ‎ 解得：‎ ‎ ∴（）‎ ‎ 令，解得 ‎ 当时，‎ ‎ 答：当小聪与小明迎面相遇时，他们离学校的路程是‎3千米。‎ ‎24、解：（1）∵直径AB⊥DE y C O P B F E D 第24题 ‎ ∴‎ ‎ ∵DE平分AO ‎ ∴‎ ‎ 又∵‎ ‎ ∴‎ ‎ 在Rt△COE中，‎ ‎ ∴⊙O的半径为2。‎ ‎ （2）连结OF ‎ 在Rt△DCP中，∵‎ ‎ ∴‎ ‎ ∴‎ ‎ ∵‎ ‎25、解：（1）‎ ‎ （2）（2，）‎ ‎ （3）①略 ‎ ②过点E作EM⊥直线CD于点M ‎∵CD∥AB x C D A O B E y ‎（图3）‎ Ｍ ‎∴‎ ‎∴‎ ‎∵‎ ‎∴‎ ‎∵△DHE∽△DEG ‎∴即 当点H在点G的右侧时，设，‎ ‎∴‎ 解：‎ ‎∴点F的坐标为（，0）‎ 当点H在点Ｇ的左侧时，设，‎ ‎∴‎ 解：，（舍）‎ ‎∵△ＤＥＧ≌△ＡＥＦ ‎∴‎ ‎∵‎ ‎∴点Ｆ的坐标为（，0）‎ 综上可知，点Ｆ的坐标有两个，分别是（，0），（，0）‎