中考数学模拟试题及答案三十三 10页

中考数学模拟试题及答案三十三 一、选择题（每小题4分 共40分）‎ ‎1.一个数的相反数是3，则这个数是 （ ）‎ ‎ A． B．－ C．－3 D．3‎ ‎2.今年1至4月份，福建省旅游业一直保持良好的发展势头，旅游收入累计达4785000000元，用科学记数法表示是 （ ）‎ ‎ A. 4785×106元 B. 4.785×108元 C. 4.785×109元 D. 4.785×1010元 ‎3.下列计算正确的是 （ ）‎ ‎ A．a3·a2＝ a5 B. a3÷a＝a ‎3 ‎ C. (a2)3 ＝ a 5 D. (‎3a)3＝‎3a 3‎ ‎4.如图所示的正四棱锥的俯视图是 （ ）‎ ‎·‎ A B C D ‎5‎ ‎5、方程x2＝2x的解是 （ ）‎ ‎ A. x＝2 B. x＝‎0 ‎ C. x1＝0，x2＝2 D. x1=2，x2＝－2‎ ‎6.在漳州市2012年中学生田径运动会上，参加男子跳高的15名运动员的成绩如下表：‎ 跳高成绩(m)‎ ‎1.50‎ ‎1.55‎ ‎1.60‎ ‎1.65‎ ‎1.70‎ ‎1.75‎ 跳高人数 ‎1‎ ‎3‎ ‎2‎ ‎3‎ ‎5‎ ‎1‎ 这些运动员跳高成绩的中位数和众数分别是 （ ）‎ O B A P 第7题图 ‎ A．1.65，1.70 B．1.70，‎1.65 ‎ C．1.70，1.70 D．3，5‎ ‎7.如图，P是Rt△ABC斜边AB上任意一点（A，B两点除外），过P点作一直线，使截得的三角形与Rt△ABC相似，这样的直线可以作（　 ）‎ ‎ A．1条 B．2条 C．3条 D．4条 A B C O ‎（第9题）‎ ‎8.下列各点中，在函数y＝图象上的点是 （ ）‎ ‎ A．(2，4) B．(－1，2) ‎ ‎ C．(－2，－1) D．(－，－1)‎ ‎9.如图，A、C、B是⊙O上三点，若∠AOC＝40°，则∠ABC的度数是（ ）‎ ‎ A．10° B．20° C．40° D．80°‎ ‎10、已知且x＋y＞0，则k的取值范围为 （　　）‎ ‎ A. k＞ B. k＜ C. k＜ D. k＞ ‎ 二、填空题（每小题4分 共24分）‎ ‎11．把一组数据中的每一个数据都减去，得一组新数据，若求得新一组数据的平均数是，方差是，则原来一组数据的平均数和方差分别为_______，________．‎ ‎12.从一副去掉大小王的扑克牌中随便拿出一张，是“K”的概率是 ‎ ‎13.在四边形ABCD中，AB=CD，BC=AD，若∠A=110°，则∠C= ‎ ‎14.用同样规格的黑白两种颜色的正方形瓷砖按下图方式铺地板，则第（3）个图形中有黑色瓷砖 块，第n个图形中需要黑色瓷砖 块（用含n的代数式表示）.‎ E C B D A F G H ‎（1）‎ ‎（2）‎ ‎（3）‎ ‎……‎ ‎15. 如图，把矩形纸片ABCD沿EF折叠，∠EFB＝57°，‎ 则∠AEF的大小为___________.‎ ‎16.如图7，双曲线与直线相交于A、B两点，B点坐标 为(－2，－3)，则A点坐标为_______________．‎ 三、解答题（86分）‎ ‎17．(本题8分)计算： ＋tan45°－ |－2|.‎ ‎18. 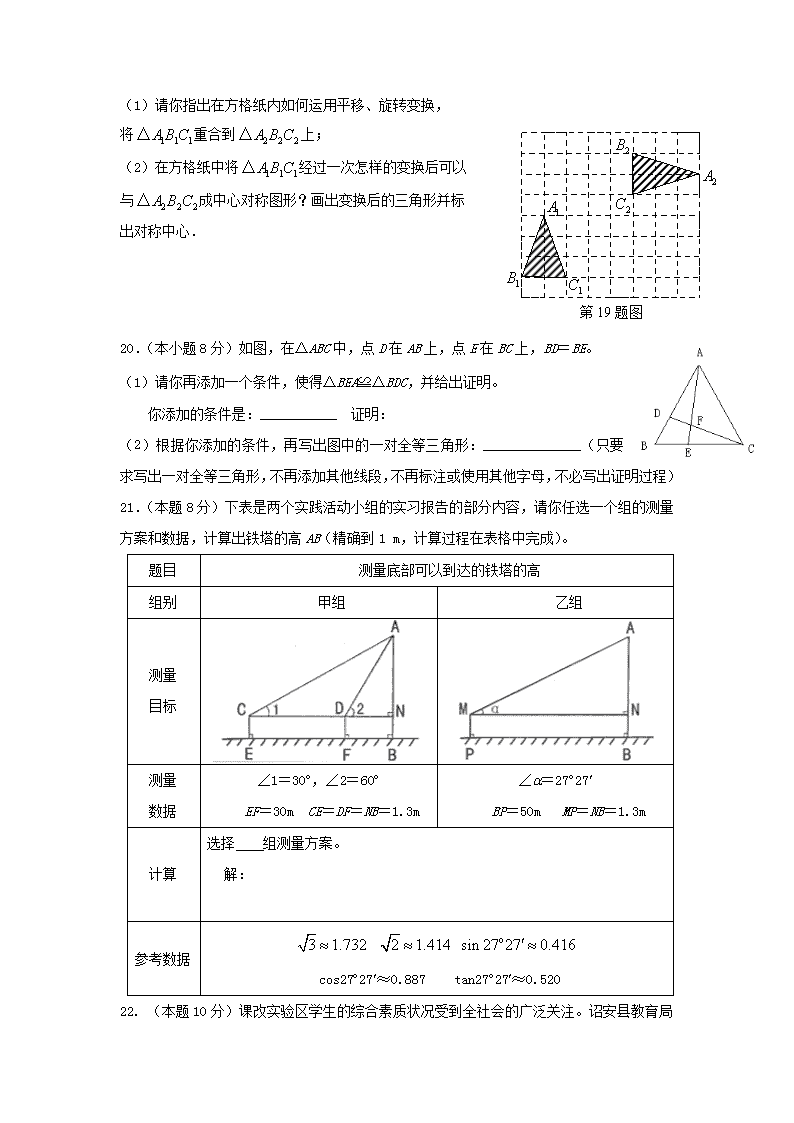（本题8分）先化简，再求值：，其中m＝－2．‎ ‎19．（本题满分10分）如图，在由边长为的小正方形组成的方格纸中，有两个全等的三角形，即和．‎ ‎（1）请你指出在方格纸内如何运用平移、旋转变换，‎ 第19题图 将重合到上；‎ ‎（2）在方格纸中将经过一次怎样的变换后可以 与成中心对称图形？画出变换后的三角形并标 出对称中心．‎ ‎20．（本小题8分）如图，在△ABC中，点D在AB上，点E在BC上，BD＝BE。‎ ‎（1）请你再添加一个条件，使得△BEA≌△BDC，并给出证明。‎ 你添加的条件是：___________ 证明：‎ ‎（2）根据你添加的条件，再写出图中的一对全等三角形：______________（只要求写出一对全等三角形，不再添加其他线段，不再标注或使用其他字母，不必写出证明过程）‎ ‎21．（本题8分）下表是两个实践活动小组的实习报告的部分内容，请你任选一个组的测量方案和数据，计算出铁塔的高AB（精确到‎1 m，计算过程在表格中完成）。‎ 题目 测量底部可以到达的铁塔的高 组别 甲组 乙组 测量 目标 测量 数据 ‎∠1＝30°，∠2＝60°‎ EF＝‎30m CE＝DF＝NB＝‎‎1.3m ‎∠a＝27°27¢‎ BP＝‎50m MP＝NB＝‎‎1.3m 计算 选择 组测量方案。‎ 解：‎ 参考数据 ‎ cos27°27¢≈0.887 tan27°27¢≈0.520‎ ‎22.‎ ‎ （本题10分）课改实验区学生的综合素质状况受到全社会的广泛关注。诏安县教育局对全县9200名学生数学学业考试状况进行了一次抽样调查，从中随机抽查了5所初中九年级全体学生的数学调考成绩，右图是2011年5月抽样情况统计图。这5所初中的九年级学生的得分情况如下表（数学学业考试满分120分）‎ 分数段 频数 频率 ‎72分以下 ‎736‎ ‎0.4‎ ‎72～80分 ‎276‎ ‎0.15‎ ‎81～95分 ‎96～108分 ‎300‎ ‎0.2‎ ‎109～119分 ‎120分 ‎5‎ ‎（1）这5所初中九年级学生的总人数有多少人？‎ ‎（2）统计时,老师漏填了表中空白处的数据，请你帮老师填上;‎ ‎（3）随机抽取一人，恰好是获得120分的概率是多少？‎ ‎（4）从上表中，你还能获得其它的信息吗?（写出一条即可）。‎ ‎23．（本小题10分）职业中专科技夏令营的学生在3位老师的带领下，准备赴北京大学参观，体验大学生活．现有两家旅行社前来洽谈，报价均为每人2000元，且各有优惠．康华旅行社表示：带队老师免费，学生按8折收费；假日旅行社表示师生一律按7折收费．经核算发现，参加两家旅行社的实际费用正好相等．‎ ‎（1）职业中专参加科技夏令营的学生共有多少人？ ‎ ‎（2）如果又增加了部分学生，职业中专应选择哪家旅行社？为什么？‎ ‎24.（本小题10分） 如图，在矩形ABCD中，AB = ‎6米，BC = ‎8米，动点P以‎2米/秒的速度从点A出发，沿AC向点C移动，同时动点Q以‎1米/秒的速度从点C出发，沿CB向点B移动，设P、Q两点移动t秒（0＜t＜5）后，四边形ABQP的面积为S米2．‎ A D B C P Q ‎⑴ 求面积S关于时间 t 的函数关系式；‎ ‎⑵ 在P、Q两点移动的过程中，四边形ABQP与△CPQ的面积能否相等？若能，求出此时点P 的位置；若不能，请说明理由．‎ ‎25．（本小题14分）如图，一次函数y＝x＋m图象过点A（1，0），交y轴于点B，C为y轴负半轴上一点，且BC＝2OB，过A、C两点的抛物线交直线AB于点D，且CD∥x轴.‎ ‎（1）求这条抛物线的解析式；‎ O O A D B C x ‎ y ‎（2）观察图象，写出使一次函数值小于二次函数值时x的取值范围； ‎ ‎（3）在题中的抛物线上是否存在一点M，使得∠ADM为直角？ ‎ 若存在，求出点M的坐标；若不存在，请说明理由.‎ ‎ ‎ 参考答案 一、选择题：C,C,A,D,C,A,C,C,B,D 二、填空题11、81.2 4.4 12、 13、110° 14、10 3n+1 15、123° 16、(2,3)‎ 三、解答题 ‎17、解： +tan45°- |-2|.‎ ‎=1+3×2+1-2………………4分 ‎ =4-2………………6分 ‎ =2………………8分 ‎18、解：………………2分 ‎＝………………4分 ‎＝．………………6分 当m＝－2时，原式＝．………………8分 ‎19，解：（1）将向上平移个单位，再向右平移个单位，然后绕点顺时针旋转． （6分）‎ ‎（2）将逆时针旋转得，与关于点中心对称．‎ ‎ （10分）‎ 第19题图 ‎4‎ ‎2‎ ‎3‎ ‎1‎ ‎（正确画出得3分）‎ ‎20、解：(1)添上的条件可以是：∠BAE=∠BCD或AB=BC或∠BDC=∠BEA………2分 证明分别用AAS,SAS,ASA. ………6分 ‎ (2) △ADF≌△CEF,或△ADC≌△CEA…8分 ‎21、（本小题8分）解： 甲组 在Rt△CAN中，tan∠1=‎ 在Rt△ADN中，tan∠2=………………3分 ∵CN-DN=CD ‎ ‎∴-=30………………6分 解得AN≈26.0‎ ‎∴AB=AN+NB≈‎27m .....................8分 乙组 在Rt△AMN中，‎ ‎∴AN=MN·tan∠α............3分 　　=50·tan27°27′ 　　≈50×0.520 　　=26.0.....................6分 ∴AB=AN+NB≈‎27m ......8分 ‎22. (1)9200×20%=1840 ......2分 ‎ ‎(2)460 ;0.25; 63 ; ......5分（每格1分）‎ ‎（3） ......7分 ‎(4)优秀率、及格率等,只要合理即可......10分 ‎23. 解：（1）设共有学生x人，康华旅行社费用为y1元，假日旅行社费用为y2元．‎ ‎……………1分 根据题意得：，即；‎ ‎，即．‎ 当y1＝y2时，即1600x＝1400x＋4200，………………5分 解得x＝21．………………7分 所以职业中专参加科技夏令营的学生共有21人．………………8分 ‎（2）y1－y2＝200 x－4200．当x＞21时，y1－y2＞0，即y1＞y2．‎ 所以如果增加部分学生，职业中专应选择假日旅行社．………………10分 ‎24、解： ‎A D B C P Q E ‎：⑴ 过点P作PE⊥BC于E，　　　　　　　　　　　　　　　　　　　 ‎ ‎ Rt△ABC中，AC＝ ＝ ＝10（米） ‎ ‎　　　　 由题意知：AP＝2t，CQ＝t，则PC＝10－2t ‎ ‎　　　　 由AB⊥BC，PE⊥BC得PE∥AB ‎ ‎ ∴ ＝ ‎ ‎　　　　 即： ＝ ‎ ‎∴ PE＝（10－2t）＝－ t＋6 ………………4分 ‎ 又∵S ＝ ×6×8＝24‎ ‎ ∴S＝S －S△CPQ＝24－ · t ·（－ t＋6）＝ t2－3t＋24 ‎ S＝ t2－3t＋24 ……………6分 ‎ ‎ ‎ ⑵ 假设四边 形ABQP与△CPQ的面积相等，则有： t2－3t＋24＝12，　‎ ‎ 即： t2－5t＋20＝0‎ ‎ ∵b2－‎4ac＝（－5）2－4×1×20＜0‎ ‎ ∴方程无实根 ‎ ∴ 在P、Q两点移动的过程中，四边形ABQP与△CPQ的面积不能相等。 …10分 ‎25．（1）把点A（1，0）代入y＝x＋m得m＝－1，‎ ‎ ∴y＝x－1 ‎ ‎∴点B坐标为（0，－1） ………2分 ‎∵BC＝2OB， OB＝1， ‎ ‎∴ BC＝2 ‎ ‎ ∴OC＝3 ‎ ‎ ∴ C点坐标为（0，－3）……3分 又CD∥x轴，∴点D的纵坐标为－3 代入y＝x－1得x＝－2，‎ ‎∴点D的坐标为（－2，－3）‎ 设抛物线的解析式为y＝ax2＋bx＋c，‎ 由题意得解得 ‎ ‎ ∴ y＝x2＋2x－3 ………………6分 ‎（2）x＜－2 或x＞1　　………………8分 ‎（3）∵BC＝CD＝2 , 且 CD∥x轴，‎ ‎∴△BCD 为等腰直角三角形，∠BCD＝90°……10分 又 抛物线顶点为 E（－1,－4），且E到CD的距离为1 ‎ ‎∴∠EDC＝45° ‎ ‎∴∠EDA＝90°………………12分 ‎∴存在点M（－1,－4 ）（即抛物线顶点E）使得∠ADM＝90°……14分 备注：第2小题过点D作AD的垂线交抛物线于点M也可求解，相应给分.‎