中考数学一轮复习 第1415课时 教学案无答案 5页

锐角三角函数 课题：第14课时 锐角三角函数 教学时间：‎ 教学目标： ‎ 1、 掌握直角三角形的概念、特征；熟悉勾股定理，会运用勾股定理及逆定理解决简单问题 2、 掌握锐角三角函数（sin A 、cos A 、tan A），知道30°、45°、60°的三角函数值，会用计算器由已知锐角求它的三角函数值，由已知三角函数值求它对应的锐角。‎ 教学重难点：会由已知条件（几何或网格）求锐角三角函数值 教学方法：‎ 教学过程：‎ ‎【复习指导】‎ 1、 锐角三角函数的意义，Rt△ABC中，设∠C＝90°，‎ ‎∠A为Rt△ABC的一个锐角，则：‎ ‎∠A的正弦 sin A＝______________；‎ ‎∠A的余弦 cos A＝______________；‎ ‎∠A的正切 tan A＝______________．‎ ‎2、30°、45°、60°的三角函数值，如下表： ‎ α sin α cos α tan α ‎30°‎ ‎45°‎ ‎60°‎ ‎3、同角三角函数之间的关系：‎ sin2α＋cos2α＝___ _____；‎ 互余两角的三角函数关系式：(α为锐角)‎ sin(90°－α)＝__ ______； cos(90°－α)＝___ _____．‎ 函数的增减性：(0°<α<90°)‎ ‎(1)sin α，tan α的值都随α______________；‎ ‎(2)cos α都随α______________．‎ ‎【预习练习】‎ 中考指要的基础演练。预习检查中对错的较多的问题进行讲解 ‎【新知探究】‎ 例1. 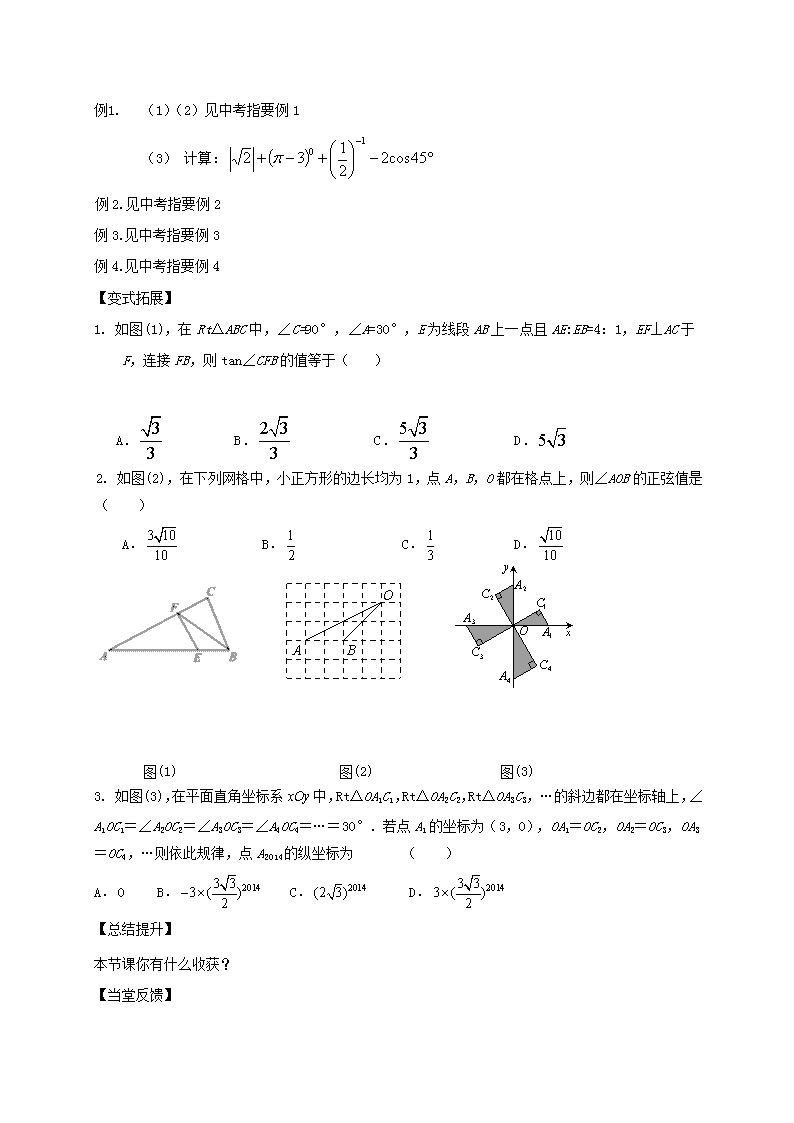‎（1）（2）见中考指要例1‎ ‎（3） 计算：‎ 例2.见中考指要例2‎ 例3.见中考指要例3 ‎ 例4.见中考指要例4‎ ‎【变式拓展】‎ ‎1. 如图(1)，在Rt△ABC中，∠C=90°，∠A=30°，E为线段AB上一点且AE:EB=4：1，EF⊥AC于F，连接FB，则tan∠CFB的值等于（ ）‎ A． B． C． D．‎ ‎2. 如图(2)，在下列网格中，小正方形的边长均为1，点A，B，O都在格点上，则∠AOB的正弦值是 （　　）‎ A． B． C． D．‎ ‎ ‎ ‎ ‎ ‎ 图(1) 图(2) 图(3)‎ ‎3. 如图(3)，在平面直角坐标系中，Rt△OA‎1C1，Rt△OA‎2C2，Rt△OA‎3C3，…的斜边都在坐标轴上，∠A1OC1＝∠A2OC2＝∠A3OC3＝∠A4OC4＝…＝30°．若点A1的坐标为（3，0），OA1＝OC2，OA2＝OC3，OA3＝OC4，…则依此规律，点A2014的纵坐标为 （　　）‎ A． ‎0 B． C． D．‎ ‎【总结提升】‎ 本节课你有什么收获？‎ ‎【当堂反馈】‎ 见中考指要的自我评估1-9‎ ‎【课后作业】‎ 见中考直通车课时练习（14）‎ 车逻初中九年级数学教案（中考一轮复习）‎ 课题：第15课时 解直角三角形 教学时间：‎ 教学目标： ‎ ‎1、能利用直角三角形的边边关系、边角关系解直角三角形。‎ ‎2、能结合仰角、俯角、坡度等知识，运用锐角三角函数解决与直角三角形有关的实际问题 教学重难点：运用锐角三角函数解决与直角三角形有关的实际问题 教学方法：‎ 教学过程：‎ ‎【复习指导】‎ ‎1．解直角三角形的定义 由直角三角形中除直角外的已知元素，求出所有未知元素的过程，叫做解直角三角形(直角三角形中，除直角外，一共有5个元素即3条边和2个锐角)．‎ ‎2．直角三角形的边角关系 在Rt△ABC中，∠C＝90°，∠A，∠B，∠C的对边分别为a，b，c.‎ ‎(1)三边之间的关系： 　；‎ ‎(2)两个锐角之间的关系： 　；‎ ‎(3)边角之间的关系：‎ sin A＝，cos A＝，tan A＝，sin B＝，cos B＝，tan B＝.‎ ‎3、解直角三角形的应用 ‎ ‎（1）．仰角、俯角：如图①，在测量时，视线与水平线所成的角中，视线在水平线上方的角叫做仰角，在水平线下方的角叫做俯角．‎ ‎（2）．坡度(坡比)、坡角：如图②，坡面的高度h和 ‎ 的比叫做坡度(或坡比)，即i＝tan α＝，坡面与水平面的夹角α叫做坡角．‎ ‎【预习练习】‎ 中考指要的基础演练；‎ ‎【新知探究】‎ 例1．‎ 例2．‎ 例3 ‎ ‎ ‎ ‎【变式拓展】‎ ‎1．如图，正方向ABCD的边长为3cm，E为CD边上一点，∠DAE=30°，M为AE的中点，过点M作直线分别与AD、BC相交于点P、Q．若PQ=AE，则AP等于　 　cm．‎ ‎2．在一次暖气管道的铺设工作中，工程由A点出发沿正西方向进行，在A点的南偏西60°方向上有一所学校B，如图，占地是以 B为中心方圆 ‎100m的圆形，当工程进行了‎200m后到达C处，此时B在C南偏西30°的方向上，请根据题中所提供的信息计算并分析一下，工程若继续进行下去是否会穿越学校。‎ ‎【总结提升】‎ 本节课你有什么收获？‎ ‎【当堂反馈】‎ 见中考指要的自我评估；‎ ‎【课后作业】‎ 见中考直通车