2019届中考数学 基础训练（3） 新版 苏科版 15页

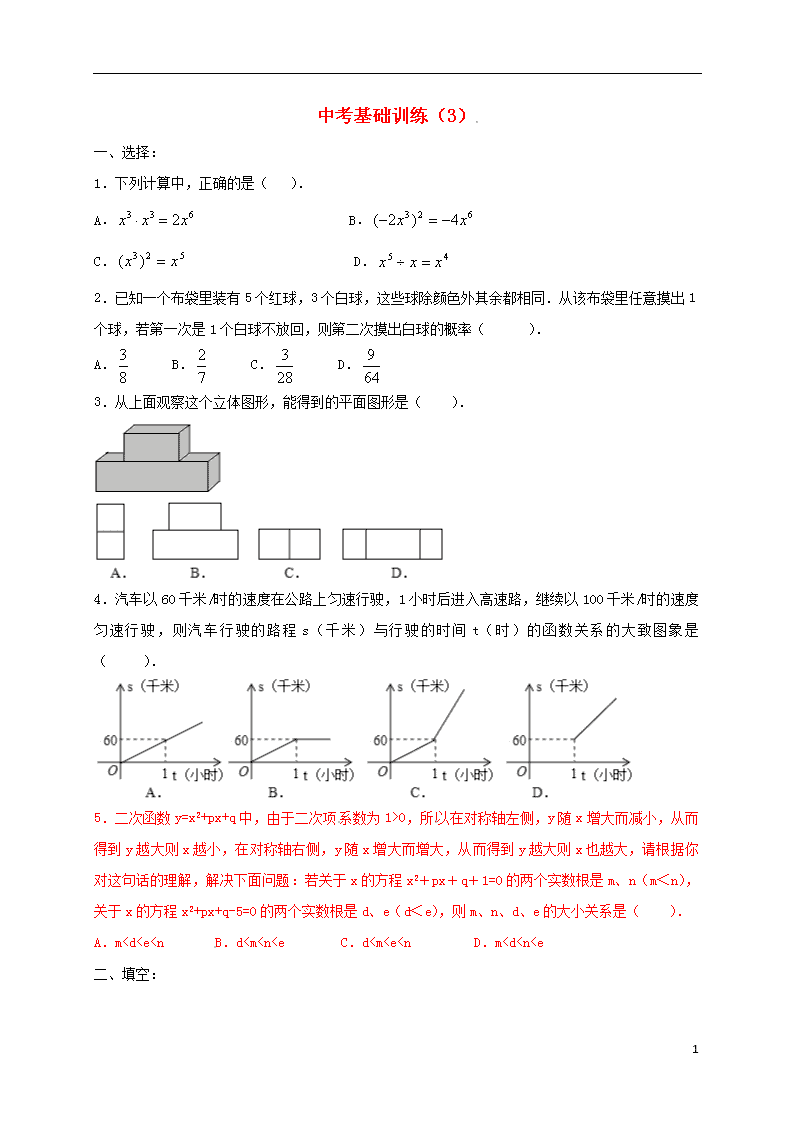
中考基础训练（3）‎ 一、选择：‎ ‎1．下列计算中，正确的是（ ）．‎ A． B．‎ C． D．‎ ‎2．已知一个布袋里装有5个红球，3个白球，这些球除颜色外其余都相同．从该布袋里任意摸出1个球，若第一次是1个白球不放回，则第二次摸出白球的概率（ ）．‎ A． B． C． D．‎ ‎3．从上面观察这个立体图形，能得到的平面图形是（ ）．‎ ‎ ‎ ‎4．汽车以60千米/时的速度在公路上匀速行驶，1小时后进入高速路，继续以100千米/时的速度匀速行驶，则汽车行驶的路程s（千米）与行驶的时间t（时）的函数关系的大致图象是（ ）．‎ ‎5．二次函数y=x2+px+q中，由于二次项系数为1>0，所以在对称轴左侧，y随x增大而减小，从而得到y越大则x越小，在对称轴右侧，y随x增大而增大，从而得到y越大则x也越大，请根据你对这句话的理解，解决下面问题：若关于x的方程x2＋px＋q＋1=0的两个实数根是m、n（m＜n），关于x的方程x2+px+q-5=0的两个实数根是d、e（d＜e），则m、n、d、e的大小关系是（ ）．‎ A．m3；由②解得：x＜5，‎ ‎∴原不等式组的解集是3＜x＜5．‎ 考点：分式方程的解法；不等式组的解法．‎ ‎20．（1）证明详见解析；（2）证明详见解析．‎ ‎【解析】‎ 试题分析：（1）根据等边对等角得到∠ACE=∠DBF，又∠E=∠F,AE=DE，根据两边及其中一边的对角对应相等的两个三角形确定可得△ACE≌△DBF；‎ ‎（2）通过证明CE∥BG，CE=BG，根据一组对边平行且相等的四边形是平行四边形即可得到四边形BGCE是平行四边形．‎ 试题解析：证明：（1）∵OB=OC，‎ ‎∴∠ACE=∠DBF，‎ 又∠E=∠F,AE=DE，‎ ‎∴△ACE≌△DBF；‎ ‎（2）∵∠ACE=∠DBF，∠DBG=∠DBF，‎ ‎∴∠ACE=∠DBG，‎ ‎∴CE∥BG，‎ ‎∵CE=BF，BG=B，‎ ‎∴CE=BG，‎ ‎∴四边形BGCE是平行四边形．‎ 考点：全等三角形的判定和性质；折叠的性质；平行四边形的判定．‎ ‎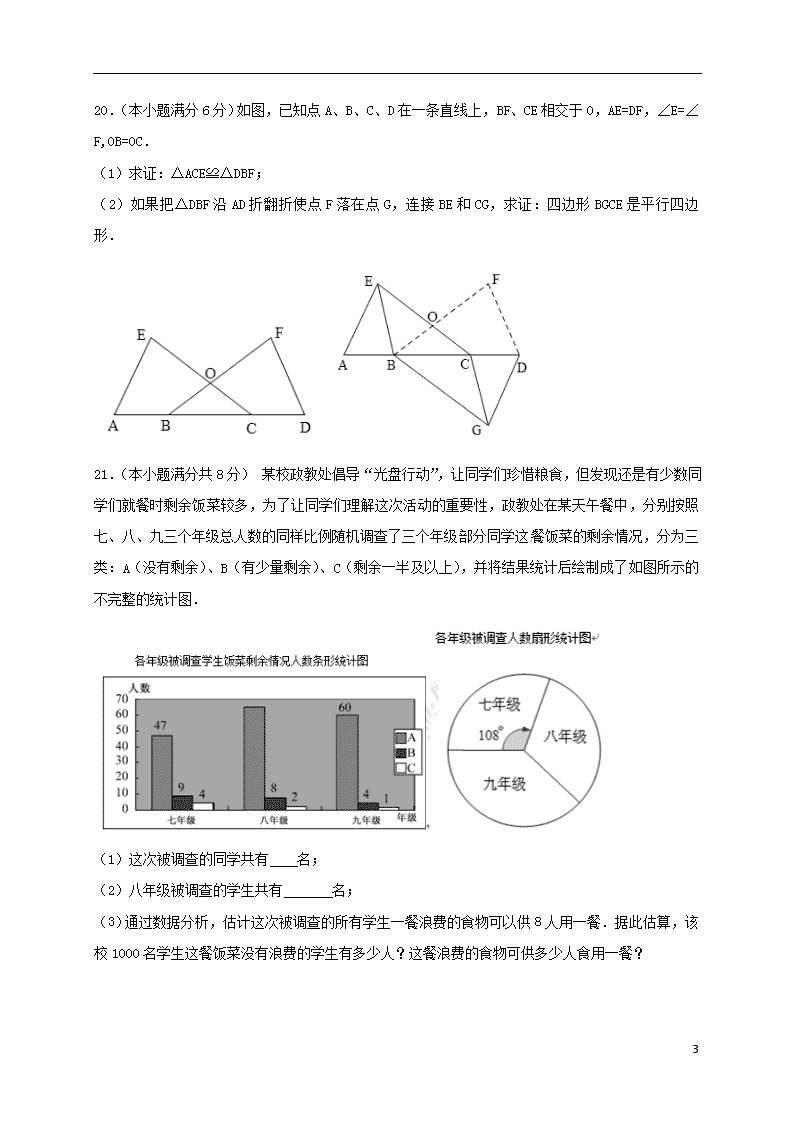21．（1）200；（2）75；（3）860； 40．‎ ‎【解析】‎ 试题分析：（1）根据七年级被调查的学生人数和所在的比例即可求出这次被调查的学生总数；‎ ‎（2）从总人数中减去七年级和九年级中被调查的学生人数，即可得到八年级被调查的学生人数；‎ ‎（3）先计算八年级没有浪费的学生人数，再计算被调查的学生中没有浪费的学生人数占被调查学生总人数的比例，利用样本估算全校没有浪费的学生人数，根据这次被调查的所有学生一餐浪费的食物可以供8人用一餐计算全校1000名学生这餐浪费的食物可供多少人食用一餐．‎ 试题解析：（1）（47+9+4）÷=200（人）．‎ 故答案为：200；‎ ‎（2）200-60-（60+4+1）=75（人）．‎ 故答案为：75；‎ ‎（3）‎75-8-2‎=65，三个年级中被调查的学生没有浪费的比例为（47+65+60）÷200=，‎ 所以全校没有浪费学生数：1000×=860（人），可共食用一餐人数：1000×=40（人）．‎ 考点：条形统计图；扇形统计图．‎ ‎22．（1）；（2）表格详见解析，．‎ ‎【解析】‎ 试题分析：（1）根据A区域与整个圆面积的比来求指针指向A区域的概率；‎ ‎（2）在甲转盘中，指针落在A区域的概率为，落在B区域的概率为，所以在甲转盘中，有一个A区域，两个B区域，在乙转盘中，指针落在A区域的概率为，落在B区域的概率为，所以在乙转盘中，有一个A区域，三个B区域，据此列表，得到共有12种可能，其中两个转盘同时指向B区域的有6种，进而得到两个转盘同时指向B区域的概率．‎ 试题解析：解：（1）指针指向A区域的概率为．‎ 故答案为：．‎ ‎（2）列表格如下：‎ ‎ P（同为B）==，‎ 所以两个转盘同时指向B区域的概率为．‎ 考点：概率公式；列表法或树状图法求概率．‎ ‎23．‎12‎米．‎ ‎【解析】‎ 试题分析：作BE⊥AC于E，设BH=x米，利用特殊角的三角函数值得到AC=3x米，BD=5x米，楼BD自身高度BD比楼AC高‎12米列关于x的方程，解得x值，进而得到两楼之间水平距离．‎ 试题解析：作BE⊥AC于E，‎ 设BH=x米，则AE=x米, BE=AH=2x米．CE=2x·米=2x米，‎ 所以AC=3x米，DH=2x·米=6x米，所以BD=5x米，‎ ‎5x-3x=12，解得x=6，‎ 所以AH=6×2=12（米）‎ 答：两楼之间水平距离‎12米．‎ 考点：解直角三角形的应用．‎ ‎24．（1）详见解析；（2）详见解析．‎ ‎【解析】‎ 试题分析：（1）利用平行线的性质可得∠CAD=∠ADO，利用等角对等边可得∠OAD=∠ADO，所以∠CAD=∠OAD；‎ ‎（2）由BD=BG得到∠BDF=∠BGD，根据AE是⊙O的直径，DF平分∠ADE，得到OF⊥AE，根据角的和差以及等量代换可以得到∠ODB=90°，即可得到BC与⊙O相切．‎ 试题解析：证明：（1）∵OD∥AC，‎ ‎∴∠CAD=∠ADO，‎ ‎∵OD=OA，‎ ‎∴∠OAD=∠ADO，‎ ‎∴∠CAD=∠OAD，‎ 即AD平分∠BAC；‎ ‎（2）连接OF，‎ ‎∵BD=BG，‎ ‎∴∠BDF=∠BGD，‎ ‎∵AE是⊙O的直径，DF平分∠ADE，‎ ‎∴OF⊥AE，‎ ‎∵∠ODB=∠ODF+∠BDF=∠OFD+∠BGD=∠OFD+∠OGF=90º，‎ ‎∴OD⊥BC，‎ ‎∴BC与⊙O相切．‎ 考点：平行线的性质；等边对等角；切线的判定．‎ ‎25．（1）2；2t；-t；1；（2）t=3，b=4．‎ ‎【解析】‎ 试题分析：（1）根据以原点O为位似中心，位似比为2:1，把△OAB放大，放大后的三角形为△OCD，所以，所以CD=2，OD=2t，据此写出点C的坐标，根据旋转的性质可知OF=OB=t，EF=AB=1，据此写出点E的坐标；‎ ‎（2）把点C和点E的坐标代入y＝x＋b得到方程组，解得b和t的值．‎ 试题解析：解：（1）根据位似图形的性质可知，，‎ 所以CD=2，OD=2t，即点C的坐标为（2，2t），‎ 根据旋转的性质可知OF=OB=t，EF=AB=1，所以点E的坐标为（-t，1）；‎ 故答案为：2；2t；-t；1；‎ ‎ （2）把点C（2，2t）和点E（-t，1）代入y＝x＋b得：‎ ‎，解得，‎ 所以t的值为3，b的值为4．‎ 考点：位似图形的性质；旋转的性质；待定系数法求解析式．‎ ‎26．（1）；（2）或；（3）存在，，．‎ ‎【解析】‎ 试题分析：（1）由点A（﹣2，0）得，由对称轴为直线x=1得，联立方程组解得a和b的值，得到抛物线的解析式；‎ ‎（2）由抛物线解析式得到点B的坐标，所以BM=3，BC=5，BP=6-3t，BQ=2t，分情况讨论，若△BPQ ‎∽△BCM ，则，若△BQP∽△BCM ， 则，分别解得t的值即可；‎ ‎（3）先求出直线BC的解析式为y=x-3 ，当t=2时，P到达终点B，BQ=4,Q（，-），然后分情况讨论，若BQ是平行四边形的边时，应用平行四边形的性质构造等式，解得点，若BQ是平行四边形的对角线时，应用平行四边形的性质构造等式，解得点．‎ 试题解析：解：（1），解得，‎ 所以抛物线的解析式为；‎ ‎（2）B（4，0），C（0-3），BM=3，BC=5，BP=6-3t，BQ=2t，‎ 若△BPQ∽△BCM ，则，得，解得，‎ 若△BQP∽△BCM ， 则，得，解得，‎ 所以当△BPQ与△BCM相似时，t的值为或；‎ ‎（3）直线BC的解析式为:y=x-3 ，当t=2时，P到达终点B，BQ=4,Q（，-），‎ 当BQ是平行四边形的边时，，‎ 当BQ是平行四边形的对角线时，，‎ 综上可知，存在，点E的坐标为，．‎ 考点：待定系数法求抛物线解析式；相似三角形的判定和性质；平行四边形的性质；待定系数法求一次函数解析式． ‎