中考数学压轴题特训详解人教新课标版 14页

中考数学压轴题汇编（1）‎ 开始 y与x的关系式 结束 输入x 输出y ‎1、（安徽）按右图所示的流程，输入一个数据x，根据y与x的关系式就输出一个数据y，这样可以将一组数据变换成另一组新的数据，要使任意一组都在20～100（含20和100）之间的数据，变换成一组新数据后能满足下列两个要求：‎ ‎（Ⅰ）新数据都在60～100（含60和100）之间；‎ ‎（Ⅱ）新数据之间的大小关系与原数据之间的大小关系一致，即原数据大的对应的新数据也较大。‎ ‎（1）若y与x的关系是y＝x＋p(100－x)，请说明：当p＝时，这种变换满足上述两个要求；‎ ‎（2）若按关系式y=a(x－h)2＋k　(a>0)将数据进行变换，请写出一个满足上述要求的这种关系式。（不要求对关系式符合题意作说明，但要写出关系式得出的主要过程）‎ ‎【解】（1）当P=时，y=x＋,即y=。‎ ‎∴y随着x的增大而增大，即P=时，满足条件（Ⅱ）……3分 又当x=20时，y==100。而原数据都在20～100之间，所以新数据都在60～100之间，即满足条件（Ⅰ），综上可知，当P=时，这种变换满足要求；……6分 ‎（2）本题是开放性问题，答案不唯一。若所给出的关系式满足：（a）h≤20；（b）若x=20,100时，y的对应值m，n能落在60～100之间，则这样的关系式都符合要求。‎ 如取h=20,y=,……8分 ‎∵a＞0，∴当20≤x≤100时，y随着x的增大…10分 令x=20,y=60，得k=60 　 ①‎ 令x=100,y=100，得a×802＋k=100 ②‎ 由①②解得， ∴。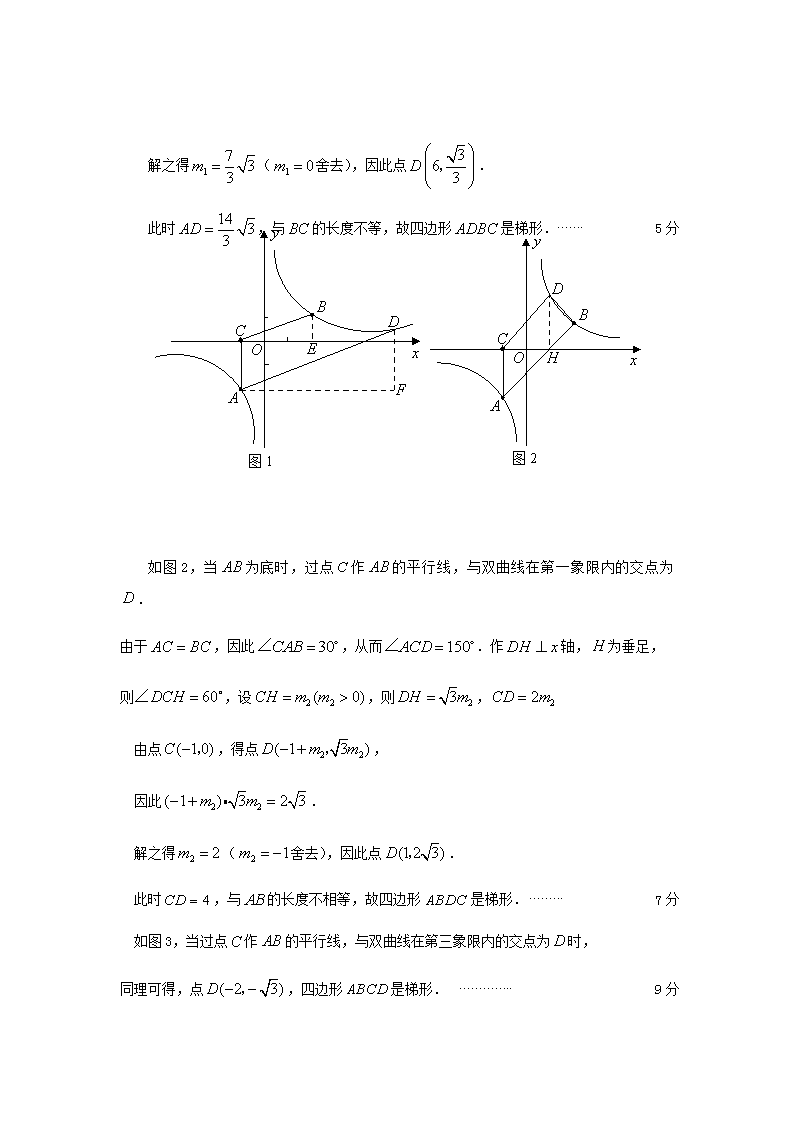………14分 ‎2、（常州）已知与是反比例函数图象上的两个点．‎ ‎（1）求的值；‎ ‎（2）若点，则在反比例函数图象上是否存在点，使得以四点为顶点的四边形为梯形？若存在，求出点的坐标；若不存在，请说明理由．‎ 解：（1）由，得，因此． 2分 ‎（2）如图1，作轴，为垂足，则，，，因此．‎ 由于点与点的横坐标相同，因此轴，从而．‎ 当为底时，由于过点且平行于的直线与双曲线只有一个公共点，‎ 故不符题意． 3分 当为底时，过点作的平行线，交双曲线于点，‎ 过点分别作轴，轴的平行线，交于点．‎ 由于，设，则，，‎ 由点，得点．‎ 因此，‎ 解之得（舍去），因此点．‎ 图2‎ 图1‎ 此时，与的长度不等，故四边形是梯形． 5分 如图2，当为底时，过点作的平行线，与双曲线在第一象限内的交点为．‎ 由于，因此，从而．作轴，为垂足，‎ 则，设，则，‎ 由点，得点，‎ 因此．‎ 解之得（舍去），因此点．‎ 此时，与的长度不相等，故四边形是梯形． 7分 如图3，当过点作的平行线，与双曲线在第三象限内的交点为时，‎ 同理可得，点，四边形是梯形． 9分 图3‎ 综上所述，函数图象上存在点，使得以四点为顶点的四边形为梯形，点的坐标为：或或． 10分 ‎3、（福建龙岩）如图，抛物线经过的三个顶点，已知轴，点在轴上，点在轴上，且．‎ ‎（1）求抛物线的对称轴；‎ ‎（2）写出三点的坐标并求抛物线的解析式；‎ ‎（3）探究：若点是抛物线对称轴上且在轴下方的动点，是否存在是等腰三角形．若存在，求出所有符合条件的点坐标；不存在，请说明理由．‎ A C B y x ‎0‎ ‎1‎ ‎1‎ 解：（1）抛物线的对称轴………2分 ‎（2） …………5分 把点坐标代入中，解得………6分 ‎…………………………………………7分 A x ‎0‎ ‎1‎ ‎1‎ Ｑ Ｎ Ｍ Ｋ y ‎（3）存在符合条件的点共有3个．以下分三类情形探索．‎ 设抛物线对称轴与轴交于，与交于．‎ 过点作轴于，易得，，，‎ ① 以为腰且顶角为角的有1个：．‎ ‎ 8分 在中，‎ ‎ 9分 ‎②以为腰且顶角为角的有1个：．‎ 在中， 10分 ‎ 11分 ‎③以为底，顶角为角的有1个，即．‎ 画的垂直平分线交抛物线对称轴于，此时平分线必过等腰的顶点．‎ 过点作垂直轴，垂足为，显然．‎ ‎．‎ ‎ 于是 13分 ‎ 14分 注：第（3）小题中，只写出点的坐标，无任何说明者不得分．‎ ‎4、（福州）如图12，已知直线与双曲线交于两点，且点的横坐标为．‎ ‎（1）求的值；‎ ‎（2）若双曲线上一点的纵坐标为8，求的面积；‎ 图12‎ ‎（3）过原点的另一条直线交双曲线于两点（点在第一象限），若由点为顶点组成的四边形面积为，求点的坐标．‎ 解：(1)∵点A横坐标为4 , ∴当 = 4时， = 2 .‎ ‎∴ 点A的坐标为（ 4，2 ）. ‎ ‎∵ 点A是直线 与双曲线 （k>0）的交点 ,‎ ‎∴ k = 4 ×2 = 8 . ‎ ‎(2) 解法一：如图12-1，‎ ‎∵ 点C在双曲线上，当 = 8时， = 1‎ ‎∴ 点C的坐标为 ( 1, 8 ) . ‎ 过点A、C分别做轴、轴的垂线，垂足为M、N，得矩形DMON .‎ S矩形ONDM= 32 ， S△ONC = 4 ， S△CDA = 9， S△OAM = 4 . ‎ S△AOC= S矩形ONDM - S△ONC - S△CDA - S△OAM = ‎32 - 4 - 9‎ - 4 = 15 . ‎ 解法二：如图12-2，‎ 过点 C、A分别做轴的垂线，垂足为E、F，‎ ‎∵ 点C在双曲线上，当 = 8时， = 1 .‎ ‎∴ 点C的坐标为 ( 1, 8 ). ‎ ‎∵ 点C、A都在双曲线上 ,‎ ‎∴ S△COE = S△AOF = 4 。 ‎ ‎∴ S△COE + S梯形CEFA = S△COA + S△AOF .‎ ‎∴ S△COA = S梯形CEFA . ‎ ‎∵ S梯形CEFA = ×（2+8）×3 = 15 , ‎ ‎∴ S△COA = 15 . ‎ ‎（3）∵ 反比例函数图象是关于原点O的中心对称图形 ,‎ ‎∴ OP=OQ，OA=OB .‎ ‎∴ 四边形APBQ是平行四边形 .‎ ‎∴ S△POA = S平行四边形APBQ = ×24 = 6 . ‎ 设点P的横坐标为（ > 0且）,‎ 得P ( , ) .‎ 过点P、A分别做轴的垂线，垂足为E、F，‎ ‎∵ 点P、A在双曲线上，∴S△POE = S△AOF = 4 .‎ 若0＜＜4，如图12-3，‎ ‎∵ S△POE + S梯形PEFA = S△POA + S△AOF,‎ ‎∴ S梯形PEFA = S△POA = 6 .‎ ‎∴ .‎ 解得= 2，= - 8(舍去) .‎ ‎∴ P（2，4）. ‎ 若 ＞ 4，如图12-4，‎ ‎∵ S△AOF+ S梯形AFEP = S△AOP + S△POE,‎ ‎∴ S梯形PEFA = S△POA = 6 .‎ ‎ ∴，‎ 解得 = 8， = - 2 (舍去) .‎ ‎∴ P（8，1）.‎ ‎∴ 点P的坐标是P（2，4）或P（8，1）. ‎ ‎5、（甘肃陇南）如图，抛物线交轴于A、B两点，交轴于点C，点P是它的 顶点，点A的横坐标是3，点B的横坐标是1．‎ ‎(1)求、的值；‎ ‎(2）求直线PC的解析式；‎ ‎(3）请探究以点A为圆心、直径为5的圆与直线 PC的位置关系，并说明理由．(参考数：，，)‎ 解： (1)由已知条件可知： 抛物线经过A(-3，0)、B(1，0)两点．‎ ‎∴ ……………………………………2分 解得 ． ………………………3分 ‎ (2) ∵， ∴ P(-1，-2)，C． …………………4分 设直线PC的解析式是，则 解得． ‎ ‎∴ 直线PC的解析式是． …………………………6分 说明：只要求对，不写最后一步，不扣分．‎ ‎ (3) 如图，过点A作AE⊥PC，垂足为E．‎ 设直线PC与轴交于点D，则点D的坐标为(3，0)． ………………………7分 在Rt△OCD中，∵ OC=，，‎ ‎∴ ． …………8分 ‎∵ OA=3，，∴AD=6． …………9分 ‎∵ ∠COD=∠AED=90o，∠CDO公用，‎ ‎∴ △COD∽△AED． ……………10分 ‎∴ ， 即． ∴ ． …………………11分 ‎∵ ，‎ ‎∴ 以点A为圆心、直径为5的圆与直线PC相离． …………12分 ‎6、（贵阳）如图14，从一个直径是2的圆形铁皮中剪下一个圆心角为的扇形．‎ ‎（1）求这个扇形的面积（结果保留）．（3分）‎ ‎（2）在剩下的三块余料中，能否从第③块余料中剪出一个圆作为底面与此扇形围成一个圆锥？请说明理由．（4分）‎ ‎（3）当的半径为任意值时，（2）中的结论是否仍然成立？请说明理由．（5分）‎ 解：（1）连接，由勾股定理求得：‎ ‎①‎ ‎②‎ ‎③‎ ‎ 1分 ‎ 2分 ‎（2）连接并延长，与弧和交于，‎ ‎ 1分 弧的长： 2分 圆锥的底面直径为： 3分 ‎，不能在余料③中剪出一个圆作为底面与此扇形围成圆锥． 4分 ‎（3）由勾股定理求得：‎ 弧的长： 1分 圆锥的底面直径为： 2分 且 ‎ 3分 即无论半径为何值， 4分 不能在余料③中剪出一个圆作为底面与此扇形围成圆锥．‎ ‎7、（河南）如图，对称轴为直线x＝的抛物线经过点A（6，0）和B（0，4）．‎ ‎（1）求抛物线解析式及顶点坐标；‎ ‎（2）设点E（x，y）是抛物线上一动点，且位于第四象限，四边形OEAF是以OA为对角线的平行四边形，求四边形OEAF的面积S与x之间的函数关系式，并写出自变量x的取值范围；‎ ‎（3）①当四边形OEAF的面积为24时，请判断OEAF是否为菱形？‎ ‎②是否存在点E，使四边形OEAF为正方形？若存在，求出点E的坐标；若不存在，请说明理由．‎ B A C D P O Q x y ‎8、（湖北黄岗）已知：如图，在平面直角坐标系中，四边形ABCO是菱形，且∠AOC=60°，点B的坐标是，点P从点C开始以每秒1个单位长度的速度在线段CB上向点B移动，设秒后，直线PQ交OB于点D.‎ ‎（1）求∠AOB的度数及线段OA的长；‎ ‎（2）求经过A，B，C三点的抛物线的解析式；‎ ‎（3）当时，求t的值及此时直线PQ的解析式；‎ ‎（4）当a为何值时，以O，P，Q，D为顶点的三角形与相似？当a 为何值时，以O，P，Q，D为顶点的三角形与不相似？请给出你的结论，并加以证明.‎ ‎9、（湖北荆门）如图1，在平面直角坐标系中，有一张矩形纸片OABC，已知O(0，0)，A(4，0)，C(0，3)，点P是OA边上的动点(与点O、A不重合)．现将△PAB沿PB翻折，得到△PDB；再在OC边上选取适当的点E，将△POE沿PE翻折，得到△PFE，并使直线PD、PF重合．‎ ‎(1)设P(x，0)，E(0，y)，求y关于x的函数关系式，并求y的最大值；‎ ‎(2)如图2，若翻折后点D落在BC边上，求过点P、B、E的抛物线的函数关系式；‎ ‎(3)在(2)的情况下，在该抛物线上是否存在点Q，使△PEQ是以PE为直角边的直角三角形？若不存在，说明理由；若存在，求出点Q的坐标．‎ 图1‎ 图2‎ 解：(1)由已知PB平分∠APD，PE平分∠OPF，且PD、PF重合，则∠BPE=90°．∴∠OPE＋∠APB=90°．又∠APB＋∠ABP=90°，∴∠OPE=∠PBA．‎ ‎∴Rt△POE∽Rt△BPA．…………………………………………………………2分 ‎∴．即．∴y=(0＜x＜4)．‎ 且当x=2时，y有最大值．…………………………………………………4分 ‎(2)由已知，△PAB、△POE均为等腰三角形，可得P(1，0)，E(0，1)，B(4，3)．……6分 设过此三点的抛物线为y=ax2＋bx＋c，则∴‎ y=．…………………………………………………………8分 ‎(3)由(2)知∠EPB=90°，即点Q与点B重合时满足条件．……………………9分 直线PB为y=x－1，与y轴交于点(0，－1)．‎ 将PB向上平移2个单位则过点E(0，1)，‎ ‎∴该直线为y=x＋1．……………………………………………………………10分 由得∴Q(5，6)．‎ 故该抛物线上存在两点Q(4，3)、(5，6)满足条件．……………………………12分