2019届中考数学一轮复习 第28课时 与圆有关的计算导学案（无答案） 4页

第28课 与圆有关的计算 姓名 班级 ‎ 学习目标：‎ ‎1. 了解正多边形的概念及正多边形与圆的关系，将正多边形问题转化为直角三角形问题．‎ ‎2. 会计算圆的弧长、扇形的面积及组合图形的周长与面积．‎ ‎3. 理解圆柱、圆锥的侧面展开图，掌握圆柱、圆锥的侧面积和全面积的计算方法．‎ 学习重难点：会计算圆的弧长、扇形的面积及组合图形的周长与面积．‎ 学习过程：‎ 一、知识梳理 ‎⑴各边________，各角_________的多边形叫做正多边形．正多边形的外接圆(或内切圆)的圆心叫做正多边形的_________．‎ ‎⑵ 正多边形都是_ _对称图形，一个正边形共有____条对称轴．如果正边形的边数为偶数，它又是____对称图形 ．‎ ‎⑶圆的有关计算公式(设半径为，圆心角的度数为)：‎ ‎① 圆周长＝_________，弧长＝______________.‎ ‎②圆面积＝______________，‎ 扇形＝___________＝____________.‎ ‎⑷圆锥：‎ ‎②圆锥的侧面展开图是一个________．‎ 这个扇形的______是圆锥的母线长，‎ 这个扇形的_______是圆锥底面圆的周长．‎ 二、典型例题 ‎1.与正多边形有关的计算 ：‎ ‎（1）(2017·北京)若正多边形的一个内角是150°，则该正多边形的边数是( )‎ A. 6 B. ‎12 ‎ C. 16 D. 18‎ ‎（2） (2017·沈阳)如图，正六边形内接于⊙，正六边形的周长是12，则 ⊙的半径是___________.‎ ‎2.与弧长有关的计算 ：‎ ‎（3）(2017·咸宁) 如图，⊙的半径为3，四边形内接于⊙，连接若，则弧的长为___________.‎ ‎（4）(2017·安顺)如图，一块含有30°角的直角三角尺，在水平桌面上绕点按顺时针方向旋转到△的位置，若，则顶点 4‎ 从开始到结束所经过的路径长为________cm.‎ ‎3．与扇形面积有关的计算： ‎ ‎ (2017·日照)如图，在四边形中，，∥，以点为圆心、为半径的圆弧与交于点，四边形是平行四边形，，则扇形(图中涂色部分)的面积是_________.‎ ‎4.与圆柱(锥)的侧面展开图有关的计算：‎ ‎（1）(2017·南通)圆锥的底面圆的半径为2，母线长为6，则侧面积为________.‎ ‎（2）(2017·苏州)如图，是⊙的直径，是弦，，.若用扇形 (图中涂色部分)围成一个圆锥的侧面，则这个圆锥底面圆的半径是_____.‎ ‎5.求阴影部分的面积 ‎ ‎(2017·济宁)如图，在△中，，将△绕点逆时针旋转30°后得到△，则图中阴影部分的面积是________.‎ 三、中考预测：‎ ‎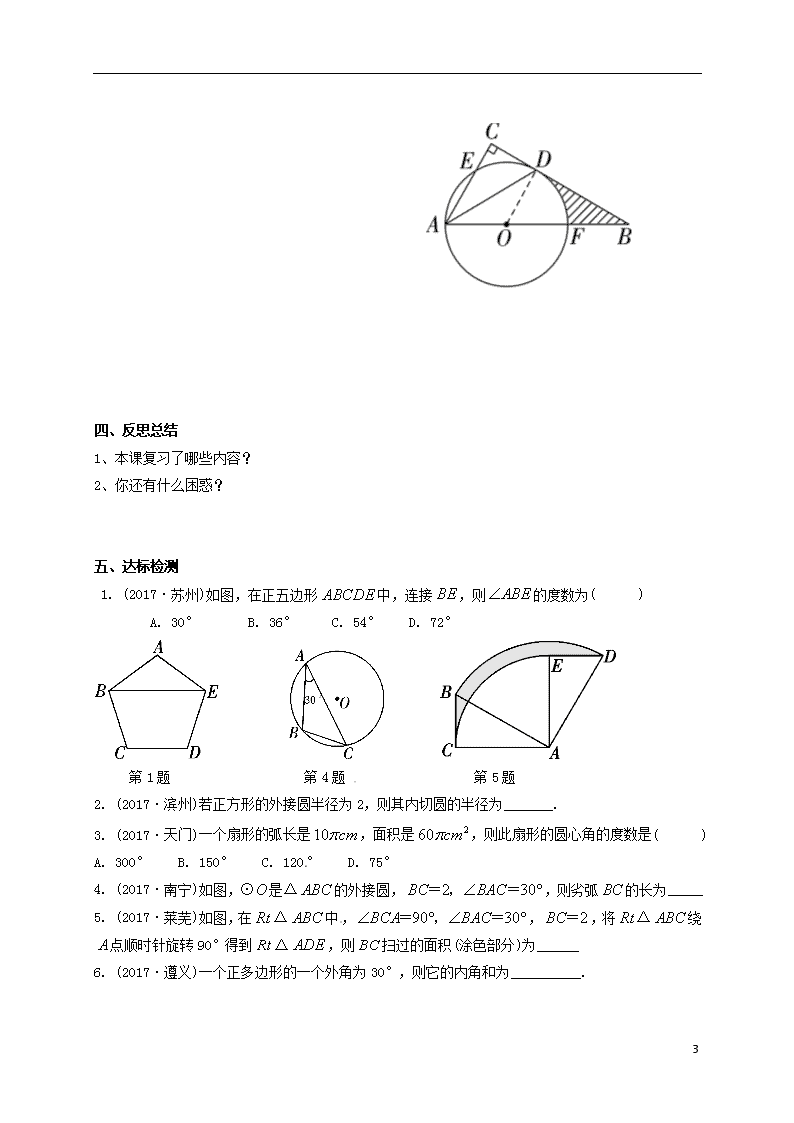1.如图，在△中，，的平分线交于点，点在上，以点为圆心、为半径的圆恰好经过点，分别交于点. ‎ ‎(1) 试判断直线与⊙的位置关系，并说明理由；‎ ‎(2) 若，，求阴影部分的面积．(结果保留)‎ 4‎ 四、反思总结 ‎1、本课复习了哪些内容？‎ ‎2、你还有什么困惑？‎ 五、达标检测 ‎ ‎ 1. (2017·苏州)如图，在正五边形中，连接，则的度数为( )‎ A. 30° B. 36° C. 54°　　D. 72°‎ ‎ ‎ ‎ 第1题 第4题 第5题 ‎2. (2017·滨州)若正方形的外接圆半径为2，则其内切圆的半径为_______.‎ ‎3. (2017·天门)一个扇形的弧长是，面积是，则此扇形的圆心角的度数是( )‎ A. 300°　　B. 150° C. 120°　　D. 75°‎ ‎4. (2017·南宁)如图，⊙是△的外接圆，，则劣弧的长为_____‎ ‎5. (2017·莱芜)如图，在△中，，，将△绕点顺时针旋转90°得到△，则扫过的面积(涂色部分)为______‎ ‎6. (2017·遵义)一个正多边形的一个外角为30°，则它的内角和为__________.‎ 4‎ ‎7. (2017·聊城)已知圆锥形工件的底面直径是，母线长，其侧面展开图圆心角的度数为________.‎ ‎8. (2017·淮安)如图，在△中，，是边上一点，以为圆心、长为半径的圆分别交于点，在的延长线上取点，使得与交于点.‎ ‎(1) 试判断直线与⊙的位置关系，并说明理由；‎ ‎(2) 若，求图中阴影部分的面积．‎ 4‎