2018中考几何最值问题规律总结 5页

你会“几何中的最值问题”吗？‎ 一、几何中最值问题包括： ①“面积最值” ②“线段（和、差）最值”.‎ ‎ （1）求面积的最值 方法：需要将面积表达成函数，借助函数性质结合取值范围求解；‎ ‎ （2）求线段及线段和、差的最值 方法：需要借助“垂线段最短”、“两点之间线段最短”及“三角形三边关系”等相关定理转化处理.‎ 一般处理方法：‎ 线段差最大 线段和(周长)最小 平移 对称 旋转 平移 对称 旋转 ‎ ‎ 使点在线同侧 ‎（如下图）‎ 使点在线异侧 ‎（如下图）‎ 三角形三边关系定理 三点共线时取得最值 两点之间，线段最短 垂线段最短 常用定理：‎ 两点之间，线段最短（已知两个定点时）‎ 垂线段最短（已知一个定点、一条定直线时）‎ 三角形三边关系 ‎|PA-PB|最大，‎ 需转化，使点在线同侧 PA+PB最小，‎ 需转化，使点在线异侧 ‎ ‎ ‎ ‎ 二、精讲精练 1. 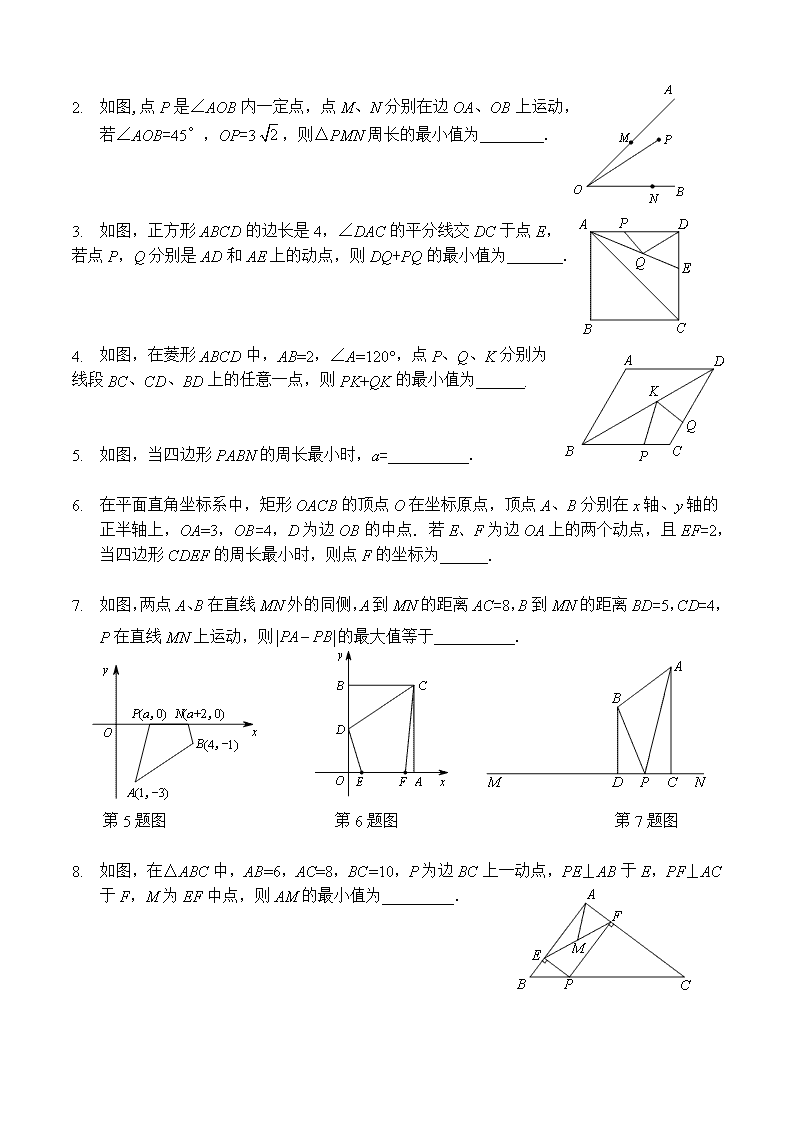如图，圆柱形玻璃杯，高为‎12cm，底面周长为‎18cm，在杯内离杯底‎4cm的点C处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿‎4cm与蜂蜜相对的点A处，则蚂蚁到达蜂蜜的最短距离为______cm．‎ 1. 如图,点P是∠AOB内一定点，点M、N分别在边OA、OB上运动，‎ 若∠AOB=45°，OP=3，则△PMN周长的最小值为 . ‎ 2. 如图，正方形ABCD的边长是4，∠DAC的平分线交DC于点E，‎ 若点P，Q分别是AD和AE上的动点，则DQ+PQ的最小值为 .‎ 3. 如图，在菱形ABCD中，AB=2，∠A=120°，点P、Q、K分别为 线段BC、CD、BD上的任意一点，则PK+QK的最小值为 .‎ 4. 如图，当四边形PABN的周长最小时，a= ．‎ 5. 在平面直角坐标系中，矩形OACB的顶点O在坐标原点，顶点A、B分别在x轴、y轴的正半轴上，OA=3，OB=4，D为边OB的中点. 若E、F为边OA上的两个动点，且EF=2，当四边形CDEF的周长最小时，则点F的坐标为 .‎ 6. 如图，两点A、B在直线MN外的同侧，A到MN的距离AC=8，B到MN的距离BD=5，CD=4，P在直线MN上运动，则的最大值等于 ．‎ 第5题图 第6题图 第7题图 ‎ 7. 如图，在△ABC中，AB=6，AC=8，BC=10，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为EF中点，则AM的最小值为_________．‎ 1. 如图，已知AB=10，P是线段AB上任意一点，在AB的同侧分别以AP和PB为边作等边△APC和等边△BPD，则CD长度的最小值为 ．‎ 2. 如图，点P在第一象限，△ABP是边长为2的等边三角形，当点A在x轴的正半轴上运动时，点B随之在y轴的正半轴上运动，运动过程中，点P到原点的最大距离是________.若将△ABP中边PA的长度改为，另两边长度不变，则点P到原点的最大距离变为_________． ‎ ‎ 第9题图 第10题图 ‎ 3. 在△ABC中，∠BAC=120°，AB=AC=4，M、N两点分别是边 AB、AC上的动点，将△AMN沿MN翻折，A点的对应 点为A′，连接BA′，则BA′的最小值是_________．‎ 几何中的最值问题（作业）‎ 1． 如图，在梯形ABCD中，AB∥CD，∠BAD=90°，AB=6，对角线AC平分∠BAD，点E在AB上，且AE=2（AE＜AD），点P是AC上的动点，则PE＋PB的最小值是__________．‎ 第1题图 第2题图 第3题图 2． 在边长为‎2cm的正方形ABCD中，点Q为BC边的中点，点P为对角线AC上一动点，连接PB、PQ，则△PBQ周长的最小值为____________cm（结果不取近似值）. ‎ 3． 如图，在锐角△ABC中，，∠BAC=45°，∠BAC的平分线交BC于点D，点M，N分别是AD和AB上的动点，则BM+MN的最小值为___________．‎ 1． ‎ 圆柱的底面周长为6cm，AC是底面圆的直径，高BC=6cm，点P是母线BC上一点，且PC= 4cm．一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是 。‎ 2． 圆柱的底面周长为6cm，AC是底面圆的直径，高BC=6cm，点P是母线BC上一点，且PC= 4cm．一只蚂蚁从圆柱外面的A点出发沿着圆柱体的表面爬行到点圆柱内侧的P的最短距离是　 ．‎ 3． 一次函数y1=kx-2与反比例函数y2=（m<0）的图象交于A，B两点，其中点A的坐标为（-6，2）‎ ‎（1）求m，k的值；‎ ‎（2）点P为y轴上的一个动点，当点P在什么位置时|PA-PB|‎ 的值最大？并求出最大值.‎ 4． 已知点A（3，4），点B为直线x=-1上的动点，设B（-1，y）．‎ ‎（1）如图1，若点C（x，0）且-1＜x＜3，BC⊥AC，求y与x之间的函数关系式；‎ ‎（2）如图2，当点B的坐标为（-1，1）时，在x轴上另取两点E，F，且EF=1．线段EF在x轴上平移，线段EF平移至何处时，四边形ABEF的周长最小？求出此时点E的坐标．‎ ‎ ‎ ‎ 图1 图2‎ ‎【精讲精练参考答案】‎ ‎1. 15 2．6 3． 4． 5． 　 6．（，0） 7．5 8．3 9． 10．5 　　 11. ； 12．2 ‎ ‎13．(1)；(2) ‎ ‎14. ‎ ‎【作业参考答案】‎ ‎1． 2． 3． 4．4　　5．2 6． ‎ ‎7．（1）；（2）当点P的坐标为（0，-10）时，|PA-PB|的最大值为；‎ ‎8．（1）；（2）．‎ ‎9.（1）；（2）；（3）‎