我的高考椭圆知识点总结 11页

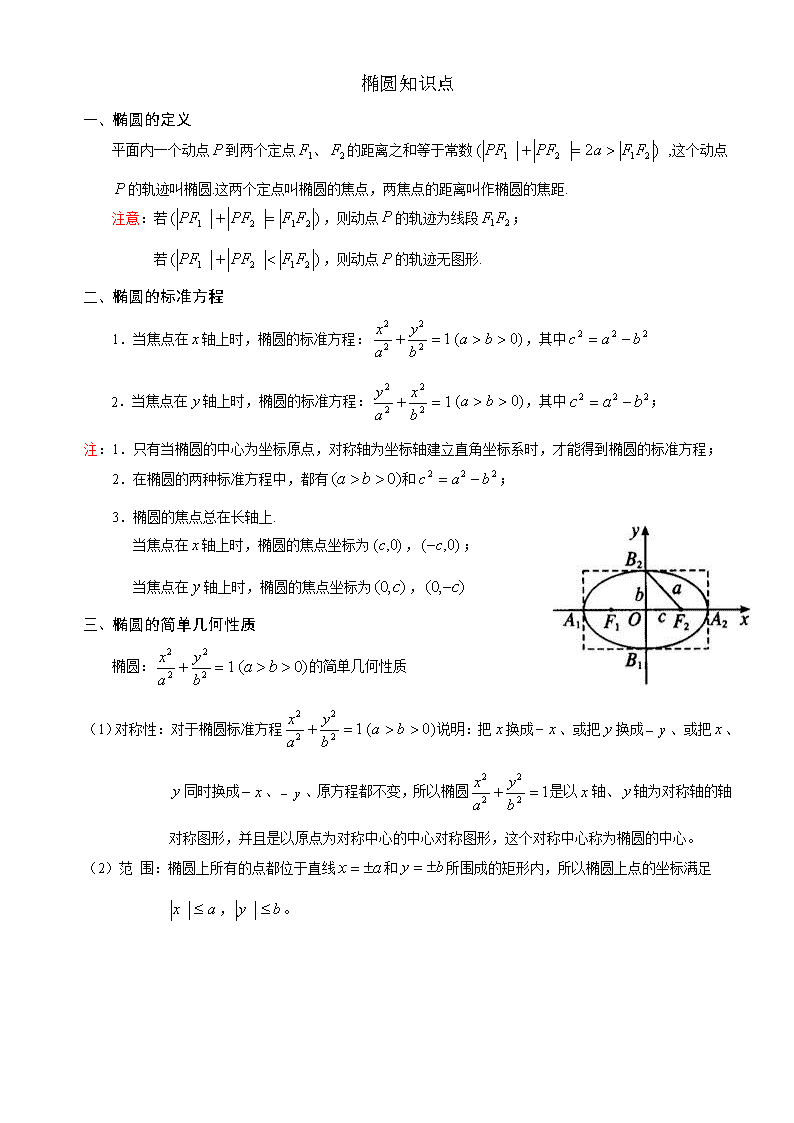
椭圆知识点 一、椭圆的定义 平面内一个动点到两个定点、的距离之和等于常数 ,这个动点的轨迹叫椭圆.这两个定点叫椭圆的焦点，两焦点的距离叫作椭圆的焦距.‎ 注意：若，则动点的轨迹为线段； 　　　　　若，则动点的轨迹无图形.‎ 二、椭圆的标准方程 　　1．当焦点在轴上时，椭圆的标准方程：，其中 ‎2．当焦点在轴上时，椭圆的标准方程：，其中；‎ 注：1．只有当椭圆的中心为坐标原点，对称轴为坐标轴建立直角坐标系时，才能得到椭圆的标准方程； 　　2．在椭圆的两种标准方程中，都有和； 　　3．椭圆的焦点总在长轴上.‎ 当焦点在轴上时，椭圆的焦点坐标为，；‎ 当焦点在轴上时，椭圆的焦点坐标为，‎ 三、椭圆的简单几何性质 　　椭圆：的简单几何性质 （1）对称性：对于椭圆标准方程说明：把换成、或把换成、或把、 ‎ 同时换成、、原方程都不变，所以椭圆是以轴、轴为对称轴的轴对称图形，并且是以原点为对称中心的中心对称图形，这个对称中心称为椭圆的中心。‎ ‎（2）范 围：椭圆上所有的点都位于直线和所围成的矩形内，所以椭圆上点的坐标满足，。‎ ‎（3）顶 点：① 椭圆的对称轴与椭圆的交点称为椭圆的顶点。 ② 椭圆与坐标轴的四个交点即为椭圆的四个顶点，坐标分别为 ‎ ‎，，，　　‎ ‎③ 线段，分别叫做椭圆的长轴和短轴，,。‎ 和分别叫做椭圆的长半轴长和短半轴长。‎ ‎（4）离心率：① 椭圆的焦距与长轴长度的比叫做椭圆的离心率，用表示，记作。 　　 ② 因为，所以的取值范围是。越接近1，则就越接近，从而 ‎ 越小，因此椭圆越扁；反之，越接近于0，就越接近0，从而越接近于，这时椭圆就越接近于圆。 当且仅当时，，这时两个焦点重合，图形变为圆，方程为。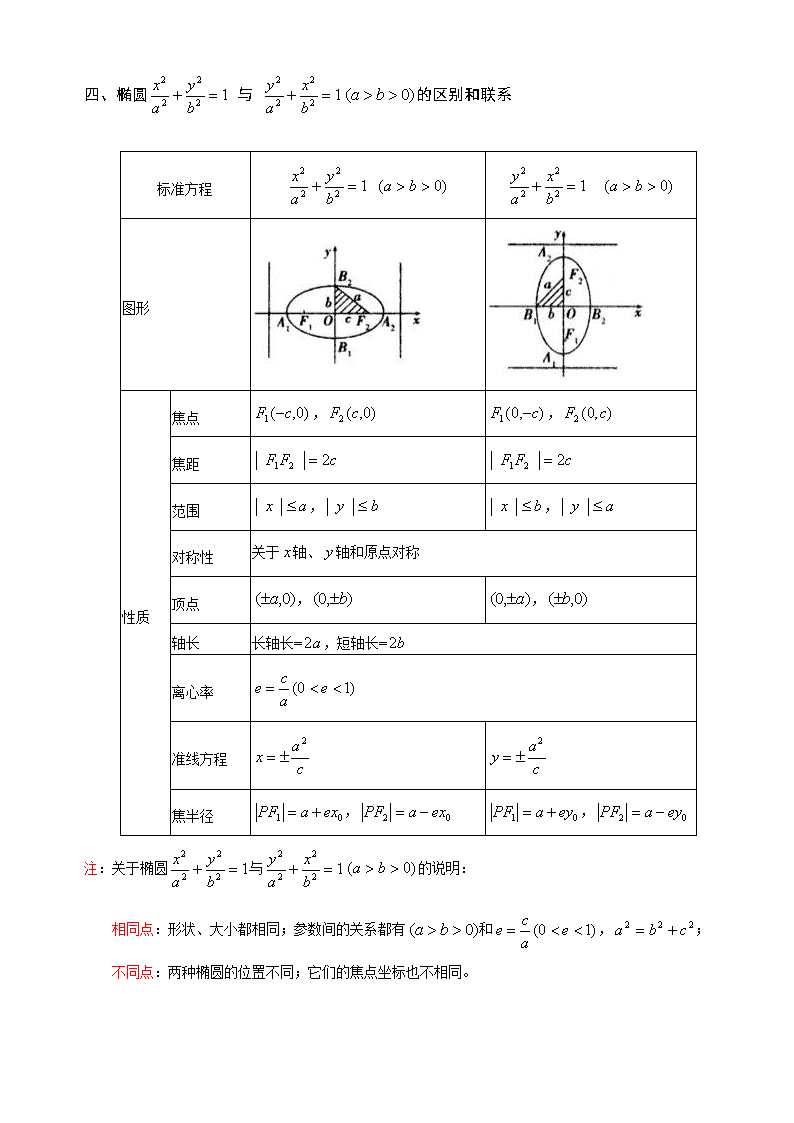‎ 注：椭圆的图像中线段的几何特征（如右图）：‎ ‎（1）；‎ ‎； （椭圆的第二定义）‎ ‎； ‎ ‎（2）； ； ； 　 （3）； ； ；‎ 四、椭圆 与 的区别和联系 标准方程 ‎ ‎ ‎ ‎ 图形 性质 焦点 ‎，‎ ‎，‎ 焦距 ‎ ‎ 范围 ‎，‎ ‎，‎ 对称性 关于轴、轴和原点对称 顶点 ‎，‎ ‎，‎ 轴长 长轴长=，短轴长= ‎ 离心率 准线方程 焦半径 ‎，‎ ‎，‎ 注：关于椭圆与的说明：‎ 相同点：形状、大小都相同；参数间的关系都有和，；‎ 不同点：两种椭圆的位置不同；它们的焦点坐标也不相同。‎ 规律方法： ‎ ‎1、如何确定椭圆的标准方程？ 　 任何椭圆都有一个对称中心，两条对称轴。当且仅当椭圆的对称中心在坐标原点，对称轴是坐标 ‎ 轴，椭圆的方程才是标准方程形式。此时，椭圆焦点在坐标轴上。‎ 确定一个椭圆的标准方程需要三个条件：‎ ‎2、椭圆标准方程中的三个量的几何意义 　　椭圆标准方程中，三个量的大小与坐标系无关，是由椭圆本身的形状大小所确定的。分别表示 ‎ 椭圆的长半轴长、短半轴长和半焦距长，均为正数，且三个量的大小关系为：，，且。‎ 可借助右图理解记忆： 　 　 　　显然：恰构成一个直角三角形的三条边，其中a是斜边，b、c为两条 ‎ 直角边。‎ ‎3、如何由椭圆标准方程判断焦点位置 ‎ 椭圆的焦点总在长轴上，因此已知标准方程，判断焦点位置的方法是：看，的分母的大小，哪个分母大，焦点就在哪个坐标轴上。‎ ‎4、方程是表示椭圆的条件 方程可化为，即，所以只有A、B、C同号，且AB时，方程表示椭圆。当时，椭圆的焦点在轴上；当时，椭圆的焦点在轴上。‎ ‎5、求椭圆标准方程的常用方法： ‎ ‎① 待定系数法：由已知条件确定焦点的位置，从而确定椭圆方程的类型，设出标准方程，再由条件确定方程中的参数的值。其主要步骤是“先定型，再定量”；‎ ‎② 定义法：由已知条件判断出动点的轨迹是什么图形，然后再根据定义确定方程。‎ ‎6．共焦点的椭圆标准方程形式上的差异 共焦点，则c相同。与椭圆共焦点的椭圆方程可设为，此类问题常用待定系数法求解。‎ ‎7．判断曲线关于轴、轴、原点对称的依据： ① 若把曲线方程中的换成，方程不变，则曲线关于轴对称；‎ ‎② 若把曲线方程中的换成，方程不变，则曲线关于轴对称；‎ ‎③ 若把曲线方程中的、同时换成、，方程不变，则曲线关于原点对称。‎ ‎8．如何求解与焦点三角形△PF‎1F2（P为椭圆上的点）有关的计算问题？ ‎ 思路分析：与焦点三角形△PF1F2有关的计算问题时，常考虑到用椭圆的定义及余弦定理（或勾股定理）、三角形面积公式相结合的方法进行计算解题。将有关线段，有关角 ()结合起来，建立、之间的关系. ‎ ‎ 焦点三角形面积公式： (P为椭圆上任一一点)‎ ‎9．如何计算椭圆的扁圆程度与离心率的关系？ 长轴与短轴的长短关系决定椭圆形状的变化。离心率，因为，，用表示为。‎ 显然：当越小时，越大，椭圆形状越扁；‎ 当越大，越小，椭圆形状越趋近于圆。‎ ‎（一）椭圆及其性质 ‎1、椭圆的定义 ‎（1）平面内与两个定点F1，F2的距离的和等于常数（大于|F1 F2|）的点的轨迹叫做椭圆，这两个定点叫椭圆的焦点，两焦点间的距离叫做椭圆的焦距。‎ ‎（2）一动点到定点的距离和它到一条定直线的距离的比是一个内常数，那么这个点的轨迹叫做椭圆 其中定点叫做焦点，定直线叫做准线，常数就是离心率 ‎2、椭圆的标准方程： ‎ ‎3、椭圆的参数方程 ‎4、离心率: 椭圆焦距与长轴长之比 ‎ ‎5、椭圆的准线方程：左准线 右准线 ‎（二）、椭圆的焦半径椭圆的焦半径公式：‎ 焦点在x轴上的椭圆的焦半径公式： （ 其中分别是椭圆的左右焦点）‎ 焦点在y轴上的椭圆的焦半径公式： （ 其中分别是椭圆的下上焦点）‎ ‎（三）、直线与椭圆问题（韦达定理的运用）‎ ‎1、弦长公式：若直线与圆锥曲线相交与、两点，‎ 则：弦长 ‎ ‎ ‎ 例1. 已知椭圆及直线y＝x＋m。‎ ‎（1）当直线和椭圆有公共点时，求实数m的取值范围；‎ ‎（2）求被椭圆截得的最长弦所在的直线的方程。‎ ‎2、已知弦AB的中点，研究AB的斜率和方程AB是椭圆＋＝1(a>b>0)的一条弦，中点M坐标为(x0，y0)，‎ 则AB的斜率为－.‎ 运用点差法求AB的斜率，设A(x1，y1)，B(x2，y2)．‎ A、 B都在椭圆上，∴ 两式相减得： ＋＝0，‎ ‎∴＋＝0，‎ 即：＝－＝－.‎ 故：kAB＝－.‎ 例2、过椭圆内一点引一条弦，使弦被点平分，求这条弦所在直线的方程。‎ ‎（四）、四种题型与三种方法 四种题型 ‎1、已知椭圆C：内有一点A（2，1），F是椭圆C的左焦点，P为椭圆C上的动点.‎ 求：｜PA｜+｜PF｜的最小值。‎ ‎2、已知椭圆内有一点A（2，1），F为椭圆的左焦点，P是椭圆上动点.‎ 求：｜PA｜+｜PF|的最大值与最小值。‎ ‎3、已知椭圆外一点A（5，6），l为椭圆的左准线，P为椭圆上动点，点P到l的距离为d，求：|PA|+的最小值。‎ ‎4、定长为d()的线段AB的两个端点分别在椭圆上移动.‎ 求：AB的中点M到椭圆右准线的最短距离。‎ 三种方法 ‎1、椭圆的切线与两坐标轴分别交于A,B两点， 求：三角形OAB的最小面积 。‎ ‎2、已知椭圆 和直线 l:x-y+9=0 ，在l上取一点M ，经过点M且以椭圆的焦 ‎ 点为焦点作椭圆，求M在何处时所作椭圆的长轴最短，并求此椭圆方程 。‎ ‎3、过椭圆的焦点的直线交椭圆A,B两点 ，求面积的最大值 。‎ ‎ ‎ 课后同步练习 ‎1. 椭圆的焦点坐标是 , 离心率是________，准线方程是_________.‎ ‎2. 已知F1、F2是椭圆的两个焦点，过F1的直线与椭圆交于M、N两点，则△MNF2的周长为( ) A．8 B．‎16 C．25 D．32‎ ‎3. 椭圆上一点P到一个焦点的距离为5，则P到另一个焦点的距离为（ ）‎ A. 5 B. 6 C. 4 D. 10‎ ‎4. 已知椭圆方程为,那么它的焦距是 （ ） ‎ A. 6 B. 3 C. 3 D. ‎ ‎5. 如果方程表示焦点在轴上的椭圆，那么实数k的取值范围是 ‎ A.（0，+∞） B. (0,2) C. (1,+∞) D. (0,1) ‎ ‎6．设为定点，||=6，动点M满足，则动点M的轨迹是（ ）‎ A. 椭圆 B. 直线 C. 圆 D. 线段 ‎ ‎7. 已知方程+=1，表示焦点在y轴上的椭圆，则m的取值范围为 .‎ ‎8. 已知椭圆的两个焦点坐标是F1（-2，0），F2（2，0），并且经过点P（），则椭圆标准方程是__ ___‎ ‎9. 过点A（-1，-2）且与椭圆的两个焦点相同的椭圆标准方程是__ __ ‎ ‎10. 过点P（，-2），Q（-2，1）两点的椭圆标准方程是_ __ ___‎ ‎11. 若椭圆的离心率是，则k的值等于 .‎ ‎12. 已知△ABC的顶点B、C在椭圆＋y2＝1上，顶点A是椭圆的一个焦点，且椭圆的另外一个焦点在BC边上，则△ABC的周长是 .‎ ‎13. F1、F2分别为椭圆+=1的左、右焦点，点P在椭圆上，△POF2是面积为的正三角形，则b2的值是 ‎ ‎14. 设M是椭圆上一点，F1、F2为焦点，，则 ‎ ‎15. 在给定椭圆中，过焦点且垂直于长轴的弦长为，焦点到相应准线的距离为1，则该椭圆的离心率为 ‎(A) (B) (C) (D) ‎ ‎16. 设是右焦点为的椭圆上三个不同的点，则“成等差数列”是“”的（ ）‎ ‎（A）充要条件 （B）必要不充分条件 ‎ ‎（C）充分不必要条件 （D）既非充分也非必要 ‎17. 如图，把椭圆的长轴分成8等份，过每个分点作轴的垂线交椭圆的上半部分于七个点，是椭圆的一个焦点，则 ‎ .‎ ‎18、已知定点A（a，0），其中，它到椭圆上的点的距离的最小值为1，求a的值。‎ ‎19、已知F1､F2是椭圆的两个焦点,P是椭圆上任一点.‎ ‎(1) 若∠F1PF2=,求△F1PF2的面积。‎ ‎(2) 求：|PF1|·|PF2|的最大值。‎