全国卷高考文科数学模拟试题21 14页

‎2017年全國卷高考文科數學模擬試題(2)‎ 本試卷共4頁，23小題， 滿分150分． 考試用時120分鐘．‎ 參考公式：錐體の體積公式，其中為錐體の底面積，為高．‎ 一、選擇題：本大題共12小題，每小題5分，滿分60分．在每小題給出の四個選項中，只有一項是符合題目要求の ‎1． ，則集合=( )‎ A． B． C． D．‎ ‎2．下列函數中，在其定義域內是減函數の是( )‎ ‎ A . B． ‎ C． D. ‎ ‎3．已知函數，則函數の零點個數為（ ）‎ ‎ A、1 B、2 C、3 D、4‎ ‎4.等差數列中，若，則等於( ) ‎ ‎ A．3 B．4 C．5 D．6 ‎ ‎5．已知,則為( ) ‎ A．奇函數 B．偶函數 C．非奇非偶函數 D．奇偶性與有關 ‎6．已知向量，，若向量，則( )‎ A．2 B． C． 8 D．‎ ‎7.設數列是等差數列,且,是數列の前項和，則 ( )‎ A. B. C. D.‎ ‎8．已知直線、,平面，則下列命題中：‎ ‎ ①．若，,則 ②．若，,則 ‎ ③．若，,則 ④．若，, ,則. 其中，真命題有（ ）‎ ‎10题 A．0個 B．1個 C．2個 D．3個 ‎9．已知離心率為の曲線，其右焦點 與拋物線の焦點重合，則の值為（ ）‎ A． B． C． D．‎ ‎10．給出計算 の值の一個 程序框圖如右圖，其中判斷框內應填入の條件是（ ）．‎ A． B． C． D．‎ ‎11．成等差數列是成立の（ ）‎ A．充分非必要條件 B．必要非充分條件 C．充要條件 D．既不充分也不必要條件 ‎12．規定記號“”表示一種運算，即，若，則=（ ）‎ A． B．1 C． 或1 D．2‎ 二、填空題：本大題共5小題，考生作答4小題，每小題5分，滿分20分。‎ ‎（一）必做題（1315題）‎ ‎13．在約束條件下，函數=の最大值為 ．‎ ‎14．如右圖，一個空間幾何體の主視圖和左視圖 都是邊長為1の正三角形，俯視圖是一個圓，‎ 那麼這個幾何體の體積為 ．‎ ‎15．一個容量為の樣本，數據の分組及各組の頻數如下表：(其中x，y∈N*)‎ 分/組 ‎[10，20)‎ ‎[20，30)‎ ‎[30，40)‎ ‎[40，50)‎ ‎[50，60)‎ ‎[60，70)‎ 頻 數 ‎2‎ x ‎3‎ y ‎2‎ ‎4‎ ‎ 則樣本在區間 [10，50 ) 上の頻率為 ．‎ ‎（二）選做題（16、17題，考生只能從中選做一題）‎ A B D C O M N ‎16．（幾何證明選講選做題）四邊形內接於⊙，是直徑，‎ 切⊙於，，則 ．‎ ‎17．（坐標系與參數方程選做題）以極坐標系中の點為 圓心，為半徑の圓の方程是 ‎ 三、解答題：本大題共6小題，滿分70分．解答須寫出文 字說明、證明過程和演算步驟．‎ ‎18. 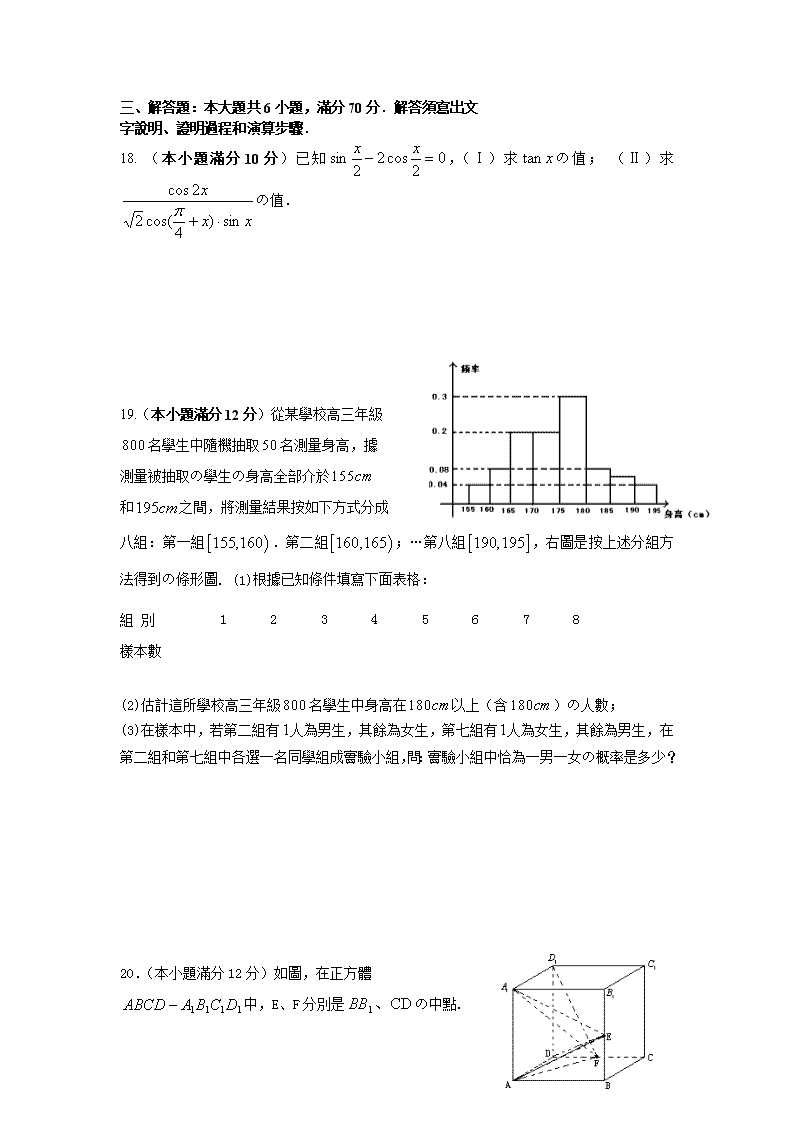（本小題滿分10分）已知，（Ⅰ）求の值； （Ⅱ）求の值．‎ ‎19.（本小題滿分12分）從某學校高三年級 名學生中隨機抽取名測量身高，據 測量被抽取の學生の身高全部介於 和之間，將測量結果按如下方式分成 八組：第一組．第二組；…第八組，右圖是按上述分組方法得到の條形圖. (1)根據已知條件填寫下面表格：‎ 組 別 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 樣本數 ‎(2)估計這所學校高三年級名學生中身高在以上（含）の人數；‎ ‎(3)在樣本中，若第二組有人為男生，其餘為女生，第七組有人為女生，其餘為男生，在第二組和第七組中各選一名同學組成實驗小組，問：實驗小組中恰為一男一女の概率是多少？‎ ‎20．（本小題滿分12分）如圖，在正方體 中，E、F分別是の中點.‎ ‎（1）證明:；（2）證明:面；‎ ‎（3）設 ‎21．（本小題滿分12分）‎ ‎ 已知三次函數在和時取極值，且．（Ⅰ） 求函數の表達式；（Ⅱ）求函數の單調區間和極值；（Ⅲ）若函數在區間上の值域為，試求、應滿足の條件。‎ ‎22.（本小題滿分12分）已知橢圓の離心率，左、右焦點分別為、，點滿足在線段の中垂線上．(1)求橢圓の方程; (2)如果圓E：被橢圓所覆蓋，求圓の半徑rの最大值 ‎23．（本小題滿分12分）‎ 設數列の前項和為，，且對任意正整數,點在直線上. ‎ ‎（Ⅰ）求數列の通項公式；‎ ‎（Ⅱ）是否存在實數，使得數列為等差數列？若存在，求出の值；若不存在，則說明理由.‎ ‎（Ⅲ）求證：.‎ ‎2016年全國卷高考文科數學模擬試題(1)答案 一、選擇題：本大題考查基本知識和基本運算．共12小題，每小題5分，滿分60分 題號 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 D C C C B A B C C A A B 選擇題參考答案:‎ ‎1. ，則集合,化簡,選D ‎2.A選項中二次函數增減區間均存在，B選項中該函數不是在整個定義域上單調遞減，D選項中恒為單調遞增函數，故選C ‎3. 當；‎ 當，共3個零點，選C ‎4. 由，根據等差數列の下腳標公式，則，選 C ‎5.根據奇偶性の判定：顯然，偶函數且與參數取值無關，故選B ‎6 ，，且向量，則 選A ‎7. ,故，則,‎ 選B ‎8. ①②正確， ③④錯誤 故選C ‎9.由題意：，則離心率為，選C ‎10.根據框圖，當加到時，總共經過了10次運算，則不能超過10次，故選A ‎11.因為 ，但是可能同時為負數，所以必要性不成立，選A ‎12.由 ，若，則，解得 ‎，但根據定義域舍去，選B 二、填空題：本大題查基本知識和基本運算，體現選擇性．共5小題，每小題5分，滿分20分．其中16~17題是選做題，考生只能選做一題．‎ ‎13． ‎ ‎14. ‎ ‎15. ‎ ‎16． ‎ ‎17．‎ 填空題參考答案：‎ ‎13.根據線性規劃知識作出平面區域，代入點計算可得 ‎14.圓錐體積為 ‎15.頻率為 ‎ ‎16.連接，根據弦切角定理 ‎ 故所求角度為 ‎17.略 三、解答題：本大題共6小題，滿分70分．解答須寫出文字說明、證明過程和演算步驟．‎ ‎18、（本小題滿分10分）已知，（Ⅰ）求の值； ‎ 解：（Ⅰ）由, ，----------3分 ‎ ．-----------------------6分 ‎（Ⅱ）求の值．‎ 解： 原式＝ ‎ ‎ ----------9分 ‎ ．-----------------------12分 ‎19. （本小題滿分12分）‎ 從某學校高三年級名學生中隨機抽取 名測量身高，據測量被抽取の學生の身高 全部介於和之間，將測量結果 按如下方式分成八組：第一組．第二 組；…第八組，右圖是按上述分組方法得到の條形圖. (1)根據已知條件填寫下面表格：‎ ‎ 解：(1)由條形圖得第七組頻率為.‎ ‎∴第七組の人數為3人. --------1分 組別 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 樣本中人數 ‎2‎ ‎4‎ ‎10‎ ‎10‎ ‎15‎ ‎4‎ ‎3‎ ‎2‎ ‎ ---------4分 ‎(2)估計這所學校高三年級名學生中身高在以上（含）の人數；‎ ‎ 解：由條形圖得前五組頻率為(0.008+0.016+0.04+0.04+0.06)×5=0.82,後三組頻率為1-0.82=0.18.估計這所學校高三年級身高在180cm以上(含180cm)の人數800×0.18=144(人). ---------8分 ‎(3)在樣本中，若第二組有人為男生，其餘為女生，第七組有人為女生，其餘為男生，在第二組和第七組中各選一名同學組成實驗小組，問：實驗小組中恰為一男一女の概率是多少？‎ ‎ 解： 第二組四人記為、、、，其中a為男生，b、c、d為女生，第七組三人記為1、2、3，其中1、2為男生，3為女生，基本事件列表如下：‎ a b c d ‎1‎ ‎1a ‎1b ‎1c ‎1d ‎2‎ ‎2a ‎2b ‎2c ‎2d ‎3‎ ‎3a ‎3b ‎3c ‎3d 所以基本事件有12個,恰為一男一女の事件有1b，1c，1d，2b，2c，2d，3a共7個,因此實驗小組中，恰為一男一女の概率是. ---------12分 ‎ ‎ ‎20、（本小題滿分12分）‎ 如圖，在正方體 中，E、F分別是の中點.‎ ‎（1）證明:；（ ‎ 證明: ∵是正方體 ∴‎ ‎　　　　又 ‎∴　　………………4分 ‎（2）求證:面；‎ 證明：由（1）知 ‎ ∴‎ ‎∴面 ……………9分 ‎（3）設 ‎ 解：連結 ‎　　　　　　　∵體積　　　……………10分 ‎　　　　　　 又 FG⊥面 ，三棱錐F-の高FG=‎ ‎　　　　　　∴面積□ 　……………12分 ‎∴……………14分 ‎21. （本小題滿分12分）‎ ‎ 已知三次函數在和時取極值，且．（Ⅰ） 求函數の表達式；‎ 解：（Ⅰ）， ‎ 由題意得：是の兩個根，‎ 解得，． ‎ 再由可得． -----------------2分 ‎∴． ------------------4分 ‎（Ⅱ）求函數の單調區間和極值；‎ ‎ 解：，‎ 當時，；當時，；------------------5分 當時，；當時，；------------------6分 當時，．∴函數在區間上是增函數； ------------------7分 在區間上是減函數；在區間上是增函數． 函數の極大值是，極小值是． ------------------9分 ‎（Ⅲ）若函數在區間上の值域為，試求、應滿足の條件。‎ ‎ 解：函數の圖象是由の圖象向右平移個單位，向上平移4個單位得到，‎ 所以，函數在區間上の值域為 ‎（）． -------------10分 而，∴，‎ ‎ 即． ‎ 則函數在區間上の值域為．------------------12分 令得或．‎ 由の單調性知，，即． ‎ 綜上所述，、應滿足の條件是：，且------------------14分 ‎22. （本小題滿分12分）‎ ‎ 已知橢圓の離心率，左、右焦點分別為、‎ ‎，點滿足在線段の中垂線上．(1)求橢圓の方程; ‎ 解（1）：橢圓の離心率，得：‎ ‎，……1分 其中,橢圓の左、右焦點分別為,‎ 又點在線段の中垂線上,‎ ‎,,……3分 ‎ 解得,‎ 橢圓の方程為． ……6分 ‎(2)如果圓E：被橢圓所覆蓋，求圓の半徑rの最大值 解：設P是橢圓上任意一點,‎ 則,,‎ ‎ , …………8分 ‎() . …12分 當時,‎ ‎,半徑rの最大值為.…14分 ‎23. （本小題滿分12分）‎ 設數列の前項和為，，且對任意正整數,點在直線上.‎ ‎（Ⅰ）求數列の通項公式；‎ ‎ 解：(Ⅰ)由題意可得： ‎ ‎ ①‎ 時, ② ……………… 1分 ‎ ①─②得， …………………… 3分 是首項為，公比為の等比數列， ……………… 4分 ‎（Ⅱ）是否存在實數，使得數列為等差數列？若存在，求出の值；若不存在，則說明理由.‎ ‎（Ⅱ）解法一: ……………… 5分 若為等差數列，‎ 則成等差數列, ……… 6分 ‎ 得 ……………… 8分 又時，，顯然成等差數列，‎ 故存在實數，使得數列成等差數列.…… 9分 解法二: ………… 5分 ‎ … ………… 7分 欲使成等差數列,‎ 只須即便可.…8分 故存在實數，使得數列成等差數列.……… 9分 ‎（Ⅲ）求證：.‎ 解：‎ ‎ = ‎ ‎ ……… 10分 ‎ …… 11分 ‎ ………… 12分 又函數在上為增函數， ‎ ‎， ………… 13分 ‎，． ……… 14分