数学高考数学试题分类汇编——三角函数 38页

2009 年高考数学试题分类汇编——三角函数 一、选择题 1.(2009 年 广 东 卷 文 ) 已 知 中 ， 的 对 边 分 别 为 若 且 ，则 A.2 B．4＋ C．4— D． 【答案】A 【解析】 由 可知, ,所以 , 由正弦定理得 ,故选 A 2.(2009 年广东卷文)函数 是 A．最小正周期为 的奇函数 B. 最小正周期为 的偶函数 C. 最小正周期为 的奇函数 D. 最小正周期为 的偶函数 【答案】A 【解析】因为 为奇函数, ,所以选 A. 3.（2009 全国卷Ⅰ理）如果函数 的图像关于点 中心对称，那么 的最小值为（C）（A） （B） （C） (D) 解: 函数 的图像关于点 中心对称 由此易得 .故选 C 4.（2009 全国卷Ⅰ理）若 ，则函数 的最大值为 。 ABC∆ CBA ∠∠∠ ,, , ,a b c 6 2a c= = + 75A∠ =  b = 2 3 2 3 6 2− 0 0 0 0 0 0 0 2 6sin sin 75 sin(30 45 ) sin30 cos45 sin 45 cos30 4A += = + = + = 6 2a c= = + 075C∠ = 030B∠ = 1sin 2B = 2 6 1sin 2sin 22 6 4 ab BA += ⋅ = × = + 1)4(cos2 2 −−= π xy π π 2 π 2 π 22cos ( ) 1 cos 2 sin 24 2y x x x π π = − − = − =   2 2T π π= = ( )cos 2y x φ＝3 ＋ 4 3 π    ，0 | |ϕ 6 π 4 π 3 π 2 π  ( )cos 2y x φ＝3 ＋ 4 3 π    ，0 42 3 k π φ π∴ ⋅ + = 42 ( )3k k Z πφ π∴ = − ⋅ ∈ min| | 3 πφ = 4 2x π π< < 3tan 2 tany x x= 解:令 , 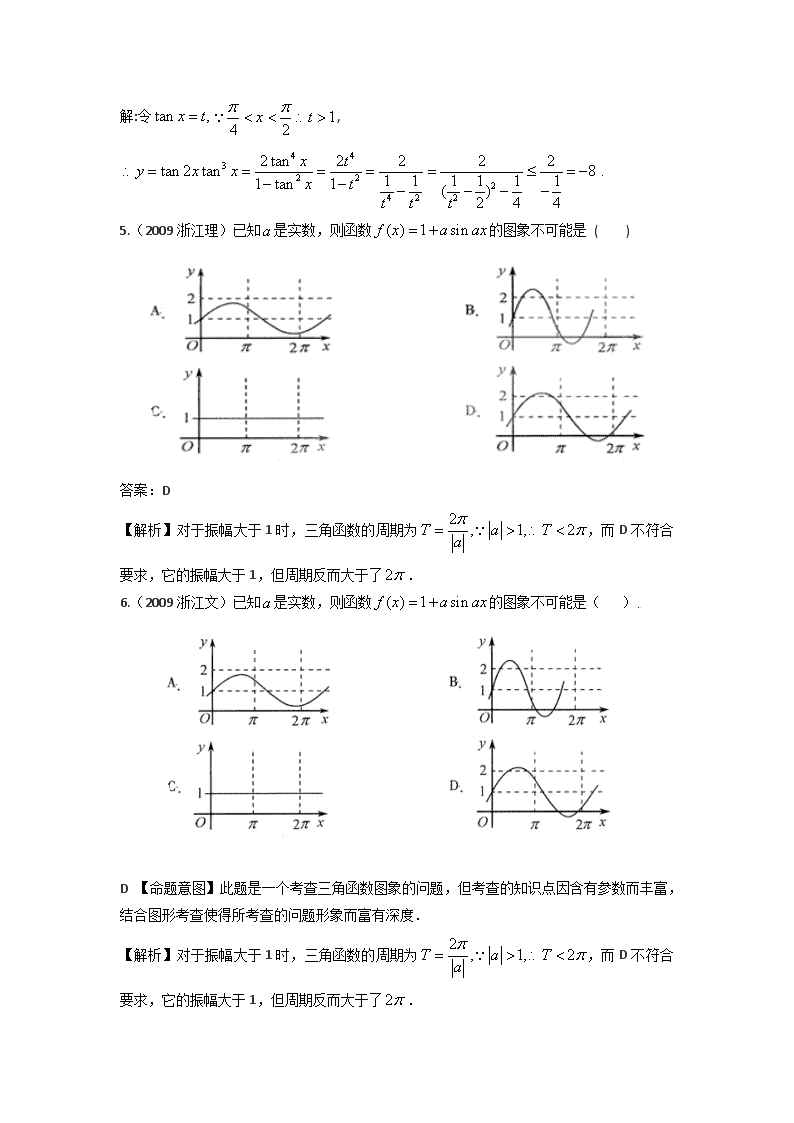5.（2009 浙江理）已知 是实数，则函数 的图象不可能是 ( ) 答案：D 【解析】对于振幅大于 1 时，三角函数的周期为 ，而 D 不符合 要求，它的振幅大于 1，但周期反而大于了 ． 6.（2009 浙江文）已知 是实数，则函数 的图象不可能是（ ） D 【命题意图】此题是一个考查三角函数图象的问题，但考查的知识点因含有参数而丰富， 结合图形考查使得所考查的问题形象而富有深度． 【解析】对于振幅大于 1 时，三角函数的周期为 ，而 D 不符合 要求，它的振幅大于 1，但周期反而大于了 ． tan ,x t= 14 2x t π π< < ∴ > 4 4 3 2 2 2 4 2 2 2tan 2 2 2 2tan 2 tan 81 1 1 1 1 11 tan 1 ( )2 4 4 x ty x x x t t t t ∴ = = = = = ≤ = −− − − − − − a ( ) 1 sinf x a ax= + 2 , 1, 2T a Ta π π= > ∴ < 2π a ( ) 1 sinf x a ax= + 2 , 1, 2T a Ta π π= > ∴ < 2π 7.（2009 北京文）“ ”是“ ”的 A． 充分而不必要条件 B．必要而不充分条件 C． 充分必要条件 D．既不充分也不必要条件 【答案】A .w【解析】本题主要考查.k本题主要考查三角函数的基本概念、简易逻辑中充要条件的判断.属 于基础知识、基本运算的考查. 当 时， ， 反之，当 时，有 ， 或 ，故应选 A. 8. （ 2009 北 京 理 ） “ ” 是 “ ” 的 （ ） A．充分而不必要条件 B．必要而不充分条件 C．充分必要条件 D．既不充分也不必要条件 【答案】A 【解析】本题主要考查三角函数的基本概念、简易逻辑中充要条件的判断. 属于基础知识、 基本运算的考查. 当 时， ， 反之，当 时，有 ， 或 ，故应选 A. 9.(2009 山东卷理)将函数 的图象向左平移 个单位, 再向上平移 1 个单位,所得 图象的函数解析式是( ). A. B. C. D. 【 解 析 】 : 将 函 数 的 图 象 向 左 平 移 个 单 位 , 得 到 函 数 即 的 图 象 , 再 向 上 平 移 1 个 单 位 , 所 得 图 象 的 函 数 解 析 式 为 ,故选 B. 答案:B 【命题立意】:本题考查三角函数的图象的平移和利用诱导公式及二倍角公式进行化简解析 式的基本知识和基本技能,学会公式的变形. 10.(2009 山东卷文)将函数 的图象向左平移 个单位, 再向上平移 1 个单位,所得 6 πα = 1cos2 2 α = 6 πα = 1cos2 cos 3 2 πα = = 1cos2 2 α = ( )2 2 3 6k k k Z π πα π α π= + ⇒ = + ∈ ( )2 2 3 6k k k Z π πα π α π= − ⇒ = − ∈ 2 ( )6 k k Z πα π= + ∈ 1cos2 2 α = 2 ( )6 k k Z πα π= + ∈ 1cos2 cos 4 cos3 3 2k π πα π = + = =   1cos2 2 α = ( )2 2 3 6k k k Z π πα π α π= + ⇒ = + ∈ ( )2 2 3 6k k k Z π πα π α π= − ⇒ = − ∈ sin 2y x= 4 π cos2y x= 22cosy x= )42sin(1 π++= xy 22siny x= sin 2y x= 4 π sin 2( )4y x π= + sin(2 ) cos22y x x π= + = 21 cos2 2cosy x x= + = sin 2y x= 4 π 图象的函数解析式是( ). A. B. C. D. 【 解 析 】 : 将 函 数 的 图 象 向 左 平 移 个 单 位 , 得 到 函 数 即 的 图 象 , 再 向 上 平 移 1 个 单 位 , 所 得 图 象 的 函 数 解 析 式 为 ,故选 A. 答案:A 【命题立意】:本题考查三角函数的图象的平移和利用诱导公式及二倍角公式进行化简解析 式的基本知识和基本技能,学会公式的变形. 11.（2009 全国卷Ⅱ文）已知△ABC 中， ，则 (A) (B) (C) (D) 答案：D 解析：本题考查同角三角函数关系应用能力，先由 cotA= 知 A 为钝角，cosA<0 排除 A 和 B，再由 选 D 12.（2009 全国卷Ⅱ文）若将函数 的图像向右平移 个单位长度 后，与函数 的图像重合，则 的最小值为 (A) (B) (C) (D) 答案：D 解析：本题考查正切函数图像及图像平移，由平移及周期性得出ωmin= 13.（2009 安徽卷理）已知函数 ， 的图像与直线 的两个相邻交点的距离等于 ，则 的单调递增区间是 （A） （B） （C） （D） [解析]： ，由题设 的周期为 ，∴ ， 由 得， ，故选 C 22cosy x= 22siny x= )42sin(1 π++= xy cos2y x= sin 2y x= 4 π sin 2( )4y x π= + sin(2 ) cos22y x x π= + = 21 cos2 2cosy x x= + = 12cot 5A = − cos A = 12 13 5 13 5 13 − 12 13 − 12 5 − 13 12cos1cossin,5 12 sin coscot 22 −==+−== AAAA AA 求得和 )0)(4tan( >+= ωπωxy 6 π )6tan( πω += xy ω 6 1 4 1 3 1 2 1 2 1 ( ) 3sin cos ( 0)f x x xω ω ω= + > ( )y f x= 2y = π ( )f x 5[ , ],12 12k k k Z π ππ π− + ∈ 5 11[ , ],12 12k k k Z π ππ π+ + ∈ [ , ],3 6k k k Z π ππ π− + ∈ 2[ , ],6 3k k k Z π ππ π+ + ∈ ( ) 2sin( )6f x x πω= + ( )f x T π= 2ω = 2 2 22 6 2k x k π π ππ π− ≤ + ≤ + ,3 6k x k k z π ππ π− ≤ ≤ + ∈ 14.（2009 安徽卷文）设函数 ，其中 ，则 导数 的取值范围是 A. B. C. D. 【解析】 ，选 D。 【答案】D 15.（2009 江西卷文）函数 的最小正周期为 A． B． C． D． 答案：A 【解析】由 可得最小正周期为 ,故选 A. 16.（2009 江西卷理）若函数 ， ，则 的最大值为 A．1 B． C． D． 答案：B 【解析】因为 = = 当 是，函数取得最大值为 2. 故选 B 17.（2009 天津卷文）已知函数 的最小正周期为 ，将 的图像向左平移 个单位长度，所得图像关于 y 轴对称，则 的一个值是（ ） A B C D 【答案】D 【解析】由已知，周期为 ，则结合平移公式和诱导公式可知平移后是偶函 数， ，故选 D 【考点定位】本试题考查了三角函数的周期性和三角函数的平移公式运用以及诱导公式的 运用。 2 1(1) sin 3 cos xf x xθ θ =′ = ⋅ + ⋅ sin 3 cos 2sin( )3 πθ θ θ= + = + 5 20, sin( ) ,1 (1) 2,212 3 2 f πθ π θ     ′∈ ∴ + ∈ ∴ ∈        ( ) (1 3 tan )cosf x x x= + 2π 3 2 π π 2 π ( ) (1 3 tan )cos cos 3sin 2sin( )6f x x x x x x π= + = + = + 2π ( ) (1 3 tan )cosf x x x= + 0 2x π≤ < ( )f x 2 3 1+ 3 2+ ( ) (1 3 tan )cosf x x x= + cos 3sinx x+ 2cos( )3x π− 3x π= )0,)(4sin()( >∈+= wRxwxxf π π )(xfy = ||ϕ ϕ 2 π 8 3π 4 π 8 π 2,2 == ww ππ xx 2cos]4)(2sin[ ±=++ πϕ 18.(2009 湖北卷理)函数 的图象 按向量 平移到 , 的函数解析 式为 当 为奇函数时，向量 可以等于 【答案】B 【 解 析 】 直 接 用 代 入 法 检 验 比 较 简 单 . 或 者 设 ， 根 据 定 义 ，根据 y 是奇函数，对应求出 ， 。 19.（2009 四川卷文）已知函数 ，下面结论错误的是 A. 函数 的最小正周期为 2 B. 函数 在区间［0， ］上是增函数 C.函数 的图象关于直线 ＝0 对称 D. 函数 是奇函数 【答案】D 【解析】∵ ，∴A、B、C 均正确，故错误的是 D 【易错提醒】利用诱导公式时，出现符号错误。 20.（2009 全国卷Ⅱ理）已知 中， ， 则 A. B. C. D. 解：已知 中， ， . 故选 D. 21. （2009 全国卷Ⅱ理）若将函数 的图像向右平移 个单位长度 后，与函数 的图像重合，则 的最小值为 A． B. C. D. 解： ， cos(2 ) 26y x π= + − F a 'F 'F ( ),y f x= ( )y f x= a .( , 2)6A π− − .( ,2)6B π− .( , 2)6C π − .( ,2)6D π ( , )a x y′ ′= cos[2( ) ] 26y y x x π′ ′− = − + − x′ y′ ))(2sin()( Rxxxf ∈−= π )(xf π )(xf 2 π )(xf x )(xf xxxf cos)2sin()( −=−= π ABC∆ 12cot 5A = − cos A = 12 13 5 13 5 13 − 12 13 − ABC∆ 12cot 5A = − ( , )2A π π∴ ∈ 2 2 1 1 12cos 1351 tan 1 ( )12 A A = − = − = − + + − ( )tan 04y x πω ω = + >   6 π tan 6y x πω = +   ω 1 6 1 4 1 3 1 2 6tan tan[ ( ] ta)64 4 6ny x y x x π π ππ πω ω ω   = + → = − = +  +     向右平移 个单位 164 ( )6 6 2k k k Z π πω π ωπ + = ∴ = + ∈∴ − 又 .故选 D 22.（2009 福建卷理）函数 最小值是 A．-1 B. C. D.1 【答案】：B [解析]∵ ∴ .故选 B 23.（2009 辽宁卷文）已知 ，则 （A） （B） （C） （D） 【解析】 ＝ ＝ 【答案】D 24.（2009 辽宁卷理）已知函数 =Acos( )的图象如图所示， ，则 = （A） (B) (C)－ (D) 【解析】由图象可得最小正周期为2π 3 于是 f(0)＝f(2π 3 ),注意到2π 3 与π 2关于 7π 12对称 所以 f(2π 3 )＝－f(π 2)＝ 【答案】B 25.（2009 辽宁卷理）已知偶函数 在区间 单调增加，则满足 ＜ 的 x 取值范围是 （A）（ ， ） (B) ［ ， ） (C)（ ， ） (D) ［ ， ） min 10 2 ω ω> ∴ = ( ) sin cosf x x x= 1 2 − 1 2 1( ) sin 22f x x= min 1( ) 2f x = − tan 2θ = 2 2sin sin cos 2cosθ θ θ θ+ − = 4 3 − 5 4 3 4 − 4 5 2 2 2 2 2 2 sin sin cos 2cossin sin cos 2cos sin cos θ θ θ θθ θ θ θ θ θ + −+ − = + 2 2 tan tan 2 tan 1 θ θ θ + − + 4 2 2 4 4 1 5 + − =+ ( )f x xω ϕ+ 2( )2 3f π = − (0)f 2 3 − 2 3 1 2 1 2 2 3 ( )f x [0, )+∞ (2 1)f x − 1( )3f 1 3 2 3 1 3 2 3 1 2 2 3 1 2 2 3 【解析】由于 f(x)是偶函数,故 f(x)＝f(|x|) ∴得 f(|2x－1|)＜f( ),再根据 f(x)的单调性 得|2x－1|＜ 解得 ＜x＜ 【答案】A 26.（2009 宁夏海南卷理）有四个关于三角函数的命题： ： x R, + = : x、y R, sin(x-y)=sinx-siny : x , =sinx : sinx=cosy x+y= 其中假命题的是 （A） ， （B） ， （3） ， （4） ， 解析： ： x R, + = 是假命题； 是真命题，如 x=y=0 时成立； 是 真命题， x , =sinx； 是假 命题， 。选 A. 27.（2009 全国卷Ⅰ文） 的值为 (A) (B) (C) (D) 【解析】本小题考查诱导公式、特殊角的三角函数值，基础题。 解： ，故选择 A。 28.（2009 全国卷Ⅰ文）已知 tan =4,cot = ,则 tan(a+ )= (A) (B) (C) (D) 【解析】本小题考查同角三角函数间的关系、正切的和角公式，基础题。 解：由题 ， ，故选择 B。 29.（2009 全国卷Ⅰ文）如果函数 的图像关于点 中心对称，那么 的最小值为 1 3 1 3 1 3 2 3 1p ∃ ∈ 2sin 2 x 2cos 2 x 1 2 2p ∃ ∈ 3p ∀ ∈ [ ]0,π 1 cos2 2 x− 4p ⇒ 2 π 1p 4p 2p 4p 1p 3p 2p 4p 1p ∃ ∈ 2sin 2 x 2cos 2 x 1 2 2p 3p ∀ ∈ [ ]0,π 21 cos2sin 0 sin sin sin2 xx x x x −≥ ∴ = = =， 4p 2 2 π ππ ≠如x= , y=2 时，si nx=cosy, 但x+y o585sin 2 2 − 2 2 3 2 − 3 2 2 245sin)45180sin()225360sin(585sin −=−=+=+= oooooo a β 1 3 β 7 11 7 11 − 7 13 7 13 − 3tan =β 11 7 121 34 tantan1 tantan)tan( −=− +=⋅− +=+ βα βαβα 3cos(2 )y x φ= + 4( ,0)3 π φ (A) (B) (C) (D) 【解析】本小题考查三角函数的图象性质，基础题。 解: 函数 的图像关于点 中心对称 由此易得 .故选 A 29.（2009 陕西卷文）若 ,则 的值为 （A）0 (B) (C)1 (D) 答案：B. 解析: 利用齐次分式的意义将分子分母同时除以 得, 故选 B. 30.（2009 四川卷文）已知函数 ，下面结论错误的是 A. 函数 的最小正周期为 2 B. 函数 在区间［0， ］上是增函数 C.函数 的图象关于直线 ＝0 对称 D. 函数 是奇函数 【答案】D 【解析】∵ ，∴A、B、C 均正确，故错误的是 D 【易错提醒】利用诱导公式时，出现符号错误。 31.（2009 湖北卷文）“sin = ”是“ ” 的 A.充分而不必要条件 B.必要而不充分条件 C.充要条件 D.既不充分也不必要条件 【答案】A 【解析】由 可得 ，故 成立的充分不必要条 件，故选 A. 32.（2009 湖北卷文）函数 的图像 F 按向量 a 平移到 F/，F/的解析式 y=f(x), 当 y=f(x)为奇函数时，向量 a 可以等于 6 π 4 π 3 π 2 π  ( )cos 2y x φ＝3 ＋ 4 3 π    ，0 42 3 2k π πφ π∴ ⋅ + = + 13 ( )6k k Z πφ π∴ = − ∈ min| | 6 πφ = tan 2α = 2 60OA OB AB AOB ο= = = ∠ = 3 4 5 4 cos (cos 0)α α ≠ 2 sin co s 2 sin co s 2 tan 1 3co s= = =sin 2 co ssin 2 co s tan + 2 4 co s α α α α αα α αα α α α − − − =++原 式 ))(2sin()( Rxxxf ∈−= π )(xf π )(xf 2 π )(xf x )(xf xxxf cos)2sin()( −=−= π α 2 1 2 12cos =α 1cos2 2a = 2 1sin 2a = ± 21 1sin sin2 4a a= =是 2)62cos( −+= π xy A. B. C. D. 【答案】D 【解析】由平面向量平行规律可知，仅当 时， ： = 为奇函数，故选 D. 33.（2009 宁夏海南卷文）有四个关于三角函数的命题： ： x R, + = : , : x , : 其中假命题的是 （A） ， （B） ， （3） ， （4） ， 【答案】A 【解析】因为 + ＝1，故 是假命题；当 x＝y 时， 成立，故 是真命题； ＝｜sinx｜，因为 x ，所以，｜sinx｜＝sinx， 正确；当 x＝ ，y＝ 时，有 ，但 ，故 假命题，选.A。 34.(2009 湖南卷理)将函数 y=sinx 的图象向左平移 0 ＜2 的单位后，得到函数 y=sin 的图象，则 等于 （D） A． B． C. D. 【答案】：D 【解析】解析由函数 向左平移 的单位得到 的图象，由条件知函数 可 化 为 函 数 ， 易 知 比 较 各 答 案 ， 只 有 ，所以选 D 项。 35.（2009 四川卷理）已知函数 ，下面结论错误的是 )2,6( −π )2,6( π )2,6( −− π )2,6( π− ( ,2)6a π= − F′ ( ) cos[2( ) ] 26 6f x x π π= + + − sin2x− 1p ∃ ∈ 2sin 2 x 2cos 2 x 1 2 2p ,x y R∃ ∈ sin( ) sin sinx y x y− = − 3p ∀ ∈ [ ]0,π 1 cos2 sin2 x x − = 4p sin cos 2x y x y π= ⇒ + = 1p 4p 2p 4p 1p 3p 2p 3p 2sin 2 x 2cos 2 x 1p 2p 2p 21 cos2 1 (1 2sin ) 2 2 x x− − −= ∈ [ ]0,π 3p 4 π 9 4 π sin cosx y= 2x y π+ > 4p ϕ ( ≤ ϕ π ) ( )6x π− ϕ 6 π 5 6 π 7 6 π 11 6 π siny x= ϕ sin( )y x ϕ= + sin( )y x ϕ= + sin( )6y x π= − 11sin( )6y x π= + sin( )6x π= − ( ) sin( )( )2f x x x R π= − ∈ A.函数 的最小正周期为 B.函数 在区间 上是增函数 C.函数 的图像关于直线 对称 D.函数 是奇函数 【考点定位】本小题考查诱导公式、三角函数的奇偶性、周期、单调性等，基础题。（同文 4） 解析：由函数的 可以得到函数 是偶函数，所以选 择 D． 36.（2009 重庆卷文）下列关系式中正确的是（ ） A． B． C． D． 【答案】C 解析因为 ，由于正弦 函 数 在 区 间 上 为 递 增 函 数 ， 因 此 ， 即 。 37.（2009 天津卷理）已知函数 的最小正周期为 ，为了 得到函数 的图象，只要将 的图象 A 向左平移 个单位长度 B 向右平移 个单位长度 C 向左平移 个单位长度 D 向右平移 个单位长度 【考点定位】本小题考查诱导公式、函数图象的变换，基础题。 解析：由题知 ，所以 ，故选择 A。 二、填空题 1.（2009 北京文）若 ，则 . 【答案】 【解析】本题主要考查简单的三角函数的运算. 属于基础知识、基本运算的考查. ( )f x 2π ( )f x 0, 2 π     ( )f x 0x = ( )f x ( ) sin( ) cos ( )2f x x x x R π= − = − ∈ ( )f x 0 0 0sin11 cos10 sin168< < 0 0 0sin168 sin11 cos10< < 0 0 0sin11 sin168 cos10< < 0 0 0sin168 cos10 sin11< < sin160 sin(180 12 ) sin12 ,cos10 cos(90 80 ) sin80° ° ° ° ° ° ° °= − = = − = siny x= [0 ,90 ]° ° sin11 sin12 sin80° ° °< < sin11 sin160 cos10° ° °< < ( ) sin( )( , 0)4f x x x R πϖ ϖ= + ∈ > π ( ) cosg x xϖ= ( )y f x= 8 π 8 π 4 π 4 π 2=ω )8(2cos)42cos()]42(2cos[)42sin()( πππππ −=−=+−=+= xxxxxf 4sin ,tan 05 θ θ= − > cosθ = 3 5 − 由已知， 在第三象限，∴ ，∴应填 . 2.（2009 江苏卷）函数 （ 为常数， ）在闭区间 上的图象如图所示，则 = . 【解析】 考查三角函数的周期知识。 ， ，所以 ， 3.（2009 湖南卷文）在锐角 中， 则 的值等于 2 ， 的取值范围为 . 解: 设 由正弦定理得 由锐角 得 ， 又 ，故 ， 4.（2009 宁夏海南卷理）已知函数 y=sin（ x+ ）（ >0, - < ）的图像如图所示， 则 =________________ 解析：由图可知， 答案： 5. （ 2009 宁 夏 海 南 卷 文 ） 已 知 函 数 的 图 像 如 图 所 示 ， 则 θ 2 2 4 3cos 1 sin 1 5 5 θ θ  = − − = − − − = −   3 5 − sin( )y A xω ϕ= + , ,A ω ϕ 0, 0A ω> > [ ,0]π− ω 3 2T π= 2 3T π= 3ω = ABC∆ 1, 2 ,BC B A= = cos AC A AC ( 2, 3) , 2 .A Bθ θ∠ = ⇒ = , 1 2.sin 2 sin 2cos cos AC BC AC AC θ θ θ θ= ∴ = ⇒ = ABC∆ 0 2 90 0 45θ θ< < ⇒ < <    0 180 3 90 30 60θ θ< − < ⇒ < <     2 330 45 cos2 2 θ θ< < ⇒ < <  2cos ( 2, 3).AC θ∴ = ∈ ω ϕ ω π ≤ ϕ π ϕ ( )5 4 4, , 2 ,12 5 5 8 9,5 10 T x π ω π ϕ ππ ϕ ϕ  = ∴ = +    + ∴ =   把 代入y=si n 有： 1=si n 9 10 π ( ) 2sin( )f x xω φ= + 。 【答案】0 【解析】由图象知最小正周期 T＝ （ ）＝ ＝ ，故 ＝3，又 x＝ 时，f （x）＝0，即 2 ）＝0，可得 ，所以， 2 ＝ 0。 6.(2009 湖南卷理)若 x∈(0, )则 2tanx+tan( -x)的最小值为 2 . 【答案】： 【 解 析 】 由 ， 知 所 以 当且仅当 时取等号，即最小值是 。 7.（2009 年上海卷理）函数 的最小值是_____________________ . 【答案】 【解析】 ，所以最小值为： 8.（2009 年上海卷理）在极坐标系中，由三条直线 ， ， 围成图形的面积是________. 【答案】 【解析】化为普通方程，分别为：y＝0，y＝ x，x＋y＝1，画出三条 直线的图象如右图，可求得 A（ ， ），B（1,0），三角形 AOB 的面积为： 7 12f π  =   3 2 44 5 ππ − 3 2π ω π2 ω 4 π φπ +× 43sin( 4 πφ = 7 12f π  =   )412 73sin( ππ +× 2 π 2 π 2 2 2 (0, )2x π∈ 1tan 0,tan( ) cot 0,2 tan πα α α α> − = = > 12tan tan( ) 2tan 2 2,2 tan πα α α α+ − = + ≥ tan 2α 2 2 22cos sin 2y x x= + 1 2− ( ) cos2 sin 2 1 2 sin(2 ) 14f x x x x π= + + = + + 1 2− 0=θ 3 πθ = 1sincos =+ θρθρ 3 3 4 − 3 2 13 − 2 33 − ＝ 9..（2009 年上海卷理）当 ，不等式 成立，则实数 的取值范围是 _______________. 【答案】k≤1 【 解 析 】 作 出 与 的 图 象 ， 要 使 不 等 式 成立，由图可知须 k≤1。 10．（2009 年上海卷理）已知函数 .项数为 27 的等差数列 满足 ，且公差 .若 ，则当 =____________ 是， . 【答案】14 【解析】函数 在 是增函数，显然又为奇函数，函数图象关于 原点对称，因为 ， 所以 ，所以当 时， . 　 11.（2009 上海卷文）函数 的最小值是 。 【答案】 【解析】 ，所以最小值为： 12.（2009 上海卷文）已知函数 。项数为 27 的等差数列 满足 且公差 ,若 ，则当 k= 时， 。 【答案】14 【解析】函数 在 是增函数，显然又为奇函数，函数图象关于 2 3312 1 −×× 3 3 4 − 时10 ≤≤ x kxx ≥ 2sin π k 2sin1 xy π= kxy =2 kxx ≥ 2sin π xxxf tansin)( += { }na     −∈ 22 ππ ，na 0≠d 0)()()( 2721 =+…++ afafaf k 0)( =kaf xxxf tansin)( += ( )2 2 π π− ， 14262271 2aaaaa =•••=+=+ 1 27 2 26 14( ) ( ) ( ) ( ) ( ) 0f a f a f a f a f a+ = + = ••• = = 14k = 0)( =kaf 2( ) 2cos sin 2f x x x= + 1 2− ( ) cos2 sin 2 1 2 sin(2 ) 14f x x x x π= + + = + + 1 2− ( ) sin tanf x x x= + { }na , ,2 2na π π ∈ −   0d ≠ 1 2 27( ) ( ) ... ( ) 0f a f a f a+ + + = ( ) 0.kf a = xxxf tansin)( += ( )2 2 π π− ， 原点对称，因为 ， 所以 ，所以当 时， .　 13.(2009 湖北卷理)已知函数 则 的值为 . 【答案】1 【解析】因为 所以 故 14.（2009 辽宁卷文）已知函数 的图象如图所示， 则 ＝ 【解析】由图象可得最小正周期为 4π 3 ∴T＝ 2π ω ＝ 4π 3 ⇒ ω＝ 【答案】 三、解答题 1.(2009 年广东卷文)（本小题满分 12 分） 已知向量 与 互相垂直，其中 （1）求 和 的值 （2）若 ， ,求 的值 【解析】（１） , ,即 又∵ , ∴ ,即 ,∴ 又　 , (2) ∵ , ,即 14262271 2aaaaa =•••=+=+ 1 27 2 26 14( ) ( ) ( ) ( ) ( ) 0f a f a f a f a f a+ = + = ••• = = 14k = 0)( =kaf ( ) '( )cos sin ,4f x f x x π= + ( )4f π '( ) '( ) sin cos4f x f x x π= − ⋅ + '( ) '( ) sin cos4 4 4 4f f π π π π= − ⋅ + '( ) 2 14f π⇒ = − ( ) '( )cos sin ( ) 14 4 4 4 4f f f π π π π π= + ⇒ = ( ) sin( )( 0)f x xω ϕ ω= + > ω 2 3 2 3 )2,(sin −= θa )cos,1( θ=b )2,0( πθ ∈ θsin θcos ϕϕθ cos53)cos(5 =− << ϕ0 2 π ϕcos a b⊥  sin 2cos 0a b θ θ∴ = − = sin 2cosθ θ= 2sin cos 1θ θ+ = 2 24cos cos 1θ θ+ = 2 1cos 5 = 2 4sin 5 θ = 2 5(0, ) sin2 5 πθ θ∈ ∴ = 5cos 5 θ = 5cos( ) 5(cos cos sin sin )θ ϕ θ ϕ θ ϕ− = + 5 cos 2 5 sinϕ ϕ= + 3 5 cosθ= cos sinϕ ϕ∴ = 2 2 2cos sin 1 cosϕ ϕ ϕ∴ = = − 2 1cos 2 ϕ = 又 , ∴ 2.（2009 全国卷Ⅰ理）（本小题满分 10 分）（注意：在试题卷上作答无效） 在 中，内角 A、B、C 的对边长分别为 、 、 ，已知 ，且 求 b 分析:此题事实上比较简单,但考生反应不知从何入手.对已知条件(1) 左 侧 是 二 次 的 右 侧 是 一 次 的 , 学 生 总 感 觉 用 余 弦 定 理 不 好 处 理 , 而 对 已 知 条 件 (2) 过多的关注两角和与差的正弦公式,甚至有的学生还想用现在 已经不再考的积化和差,导致找不到突破口而失分. 解 法 一 ： 在 中 则 由 正 弦 定 理 及 余 弦 定 理 有 : 化 简 并 整 理 得 ： . 又 由 已 知 .解得 . 解法二:由余弦定理得: .又 , 。 所以 …………………………………① 又 ， ，即 由正弦定理得 ，故 ………………………② 由①，②解得 。 评析:从 08 年高考考纲中就明确提出要加强对正余弦定理的考查.在备考中应注意总结、提 高自己对问题的分析和解决能力及对知识的灵活运用能力.另外提醒：两纲中明确不再 考的知识和方法了解就行，不必强化训练。 3.（2009 浙江理）（本题满分 14 分）在 中，角 所对的边分别为 ，且满 足 ， ． （I）求 的面积； （II）若 ，求 的值． << ϕ0 2 π 2cos 2 ϕ = ABC∆ a b c 2 2 2a c b− = sin cos 3cos sin ,A C A C= 2 2 2a c b− = sin cos 3cos sin ,A C A C= ABC∆ sin cos 3cos sin ,A C A C= 2 2 2 2 2 2 3 ,2 2 a b c b c aa cab bc + − + −=  2 2 22( )a c b− = 2 2 2a c b− = 24b b∴ = 4 0(b b= =或 舍） 2 2 2 2 cosa c b bc A− = − 2 2 2a c b− = 0b ≠ 2 cos 2b c A= + sin cos 3cos sinA C A C= sin cos cos sin 4cos sinA C A C A C∴ + = sin( ) 4cos sinA C A C+ = sin 4cos sinB A C= sin sinbB Cc = 4 cosb c A= 4b = ABC∆ , ,A B C , ,a b c 2 5cos 2 5 A = 3AB AC⋅ =  ABC∆ 6b c+ = a 解 析 ： （ I ） 因 为 ， ， 又 由 ，得 ， （ II ） 对 于 ， 又 ， 或 ， 由 余 弦 定 理 得 ， 4.（2009 浙江文）（本题满分 14 分）在 中，角 所对的边分别为 ，且满 足 ， ． （I）求 的面积； （II）若 ，求 的值． 解析：（Ⅰ） 又 ， ，而 ， 所以 ，所以 的面积为： （Ⅱ）由（Ⅰ）知 ，而 ，所以 所以 5.（2009 北京文）（本小题共 12 分）已知函数 . （Ⅰ）求 的最小正周期； （Ⅱ）求 在区间 上的最大值和最小值. 【解析】本题主要考查特殊角三角函数值、诱导公式、二倍角的正弦、三角函数在闭区间上 的最值等基础知识，主要考查基本运算能力． （Ⅰ）∵ ， ∴函数 的最小正周期为 . （Ⅱ）由 ，∴ ， ∴ 在区间 上的最大值为 1，最小值为 . 6.（2009 北京理）（本小题共 13 分） 2 5cos 2 5 A = 2 3 4cos 2cos 1 ,sin2 5 5 AA A∴ = − = = 3AB AC⋅ =  cos 3,bc A = 5bc∴ = 1 sin 22ABCS bc A∆∴ = = 5bc = 6b c+ = 5, 1b c∴ = = 1, 5b c= = 2 2 2 2 cos 20a b c bc A= + − = 2 5a∴ = ABC∆ , ,A B C , ,a b c 2 5cos 2 5 A = 3AB AC⋅ =  ABC∆ 1c = a 5 31)5 52(212cos2cos 22 =−×=−= AA ),0( π∈A 5 4cos1sin 2 =−= AA 35 3cos... === bcAACABACAB 5=bc ABC∆ 25 452 1sin2 1 =××=Abc 5=bc 1=c 5=b 5232125cos222 =×−+=−+= Abccba ( ) 2sin( )cosf x x xπ= − ( )f x ( )f x ,6 2 π π −   ( ) ( )2sin cos 2sin cos sin 2f x x x x x xπ= − = = ( )f x π 26 2 3x x π π π π− ≤ ≤ ⇒ − ≤ ≤ 3 sin 2 12 x− ≤ ≤ ( )f x ,6 2 π π −   3 2 − 在 中，角 的对边分别为 ， 。 （Ⅰ）求 的值； （Ⅱ）求 的面积. 【解析】本题主要考查三角形中的三角函数变换及求值、诱导公式、三角形的面积公式等基 础知识，主要考查基本运算能力． （Ⅰ）∵A、B、C 为△ABC 的内角，且 ， ∴ ， ∴ . （Ⅱ）由（Ⅰ）知 ， 又∵ ，∴在△ABC 中，由正弦定理，得 ∴ . ∴△ABC 的面积 . 7.（2009 江苏卷）（本小题满分 14 分） 设向量 （1）若 与 垂直，求 的值； （2）求 的最大值; （3）若 ，求证： ∥ . 【解析】 本小题主要考查向量的基本概念，同时考查同角三角函数的基本关系式、二倍角 的正弦、两角和的正弦与余弦公式，考查运算和证明得基本能力。满分 14 分。 ABC∆ , ,A B C , , , 3a b c B π= 4cos , 35A b= = sinC ABC∆ 4,cos3 5B A π= = 2 3,sin3 5C A A π= − = 2 3 1 3 4 3sin sin cos sin3 2 2 10C A A A π + = − = + =   3 3 4 3sin ,sin5 10A C += = , 33B b π= = sin 6 sin 5 b Aa B = = 1 1 6 3 4 3 36 9 3sin 32 2 5 10 50S ab C + += = × × × = (4cos ,sin ), (sin ,4cos ), (cos , 4sin )a b cα α β β β β= = = −   a 2b c−  tan( )α β+ | |b c+  tan tan 16α β = a b 8.(2009 山东卷理)(本小题满分 12 分)设函数 f(x)=cos(2x+ )+sin x. (1) 求函数 f(x)的最大值和最小正周期. (2) 设 A,B,C 为 ABC 的三个内角，若 cosB= ， ，且 C 为锐角，求 sinA. 解: （1）f(x)=cos(2x+ )+sin x.= 所以函数 f(x)的最大值为 ,最小正周期 . （2） = =－ , 所以 , 因为 C 为锐角, 所以 , 又因为在 ABC 中, cosB= , 所以 , 所以 . 【命题立意】:本题主要考查三角函数中两角和差的弦函数公式、二倍角公式、三角函数的 性质以及三角形中的三角关系. 9.(2009 山 东 卷 文 )( 本 小 题 满 分 12 分 ) 设 函 数 f(x)=2 在 处取最小值. (3) 求 .的值; (4) 在 ABC 中, 分别是角 A,B,C 的对边,已知 ,求角 C.. 解: （1） 因为函数 f(x)在 处取最小值，所以 ,由诱导公式知 ,因为 ,所以 .所以 （2）因为 ,所以 ,因为角 A 为 ABC 的内角,所以 .又因为 所以由正弦定理,得 ,也就是 , 3 π 2 ∆ 3 1 1( )2 4 cf = − 3 π 2 1 cos2 1 3cos2 cos sin 2 sin sin 23 3 2 2 2 xx x x π π −− + = − 1 3 2 + π ( )2 cf 1 3 sin2 2 C− 4 1 3sin 2C = 3C π= ∆ 3 1 2sin 33B = 2 1 1 3 2 2 3sin sin( ) sin cos cos sin 23 2 3 2 6A B C B C B C += + = + = × + × = )0(sinsincos2cossin 2 πϕϕϕ <<−+ xxx π=x ϕ ∆ cba ,, ,2,1 == ba 2 3)( =Af 1 cos( ) 2sin cos sin sin2f x x x x ϕ ϕ+= ⋅ + − sin sin cos cos sin sinx x x xϕ ϕ= + + − sin cos cos sinx xϕ ϕ= + sin( )x ϕ= + π=x sin( ) 1π ϕ+ = − sin 1ϕ = 0 ϕ π< < 2 πϕ = ( ) sin( ) cos2f x x x π= + = 2 3)( =Af 3cos 2A = ∆ 6A π= ,2,1 == ba sin sin a b A B = sin 1 2sin 2 2 2 b AB a = = × = 因为 ,所以 或 . 当 时, ;当 时, . 【命题立意】:本题主要考查了三角函数中两角和差的弦函数公式、二倍角公式和三角函数 的性质,并利用正弦定理解得三角形中的边角.注意本题中的两种情况都符合. 10.（2009 全国卷Ⅱ文）（本小题满分 12 分）设△ABC 的内角 A、B、C 的对边长分别为 a、 b、c， , ，求 B. 解析：本题考查三角函数化简及解三角形的能力，关键是注意角的范围对角的三角函数值 的制约，并利用正弦定理得到 sinB= (负值舍掉)，从而求出 B= 。 解：由 cos（A C）+cosB= 及 B=π （A+C）得 cos（A C） cos（A+C）= ， cosAcosC+sinAsinC （cosAcosC sinAsinC）= , sinAsinC= . 又由 =ac 及正弦定理得 故 ， 或 （舍去）， 于是 B= 或 B= . 又由 知 或 所 以 B = 。 11.（ 2009广 东 卷 理 ） (本小题满分12分） 已知向量 与 互相垂直，其中 ． （1）求 和 的值； b a> 4 π=B 4 3π=B 4 π=B 7 6 4 12C π π ππ= − − = 4 3π=B 3 6 4 12C π π ππ= − − = 2 3cos)cos( =+− BCA acb =2 2 3 3 π − 3 2 − − − 3 2 − − 3 2 3 4 2b 2sin sin sin ,B A C= 2 3sin 4B = 3sin 2B = 3sin 2B = − 3 π 2 3 π 2b ac= ab ≤ cb ≤ 3 π )2,(sin −= θa )cos,1( θ=b (0, )2 πθ ∈ θsin θcos （2）若 ，求 的值． 解：（1）∵ 与 互相垂直，则 ，即 ，代入 得 ， 又 ， ∴ . （ 2 ） ∵ ， ， ∴ ， 则 ， ∴ . 12.（2009 安徽卷理）（本小题满分 12 分） 在 ABC 中， , sinB= . （I）求 sinA 的值； (II)设 AC= ，求 ABC 的面积. 本小题主要考查三角恒等变换、正弦定理、解三角形等有关知识，考查运算求解能力。本小 题满分 12 分 解：（Ⅰ）由 ，且 ，∴ ，∴ ， ∴ ，又 ，∴ （Ⅱ）如图，由正弦定理得 ∴ ，又 10sin( ) ,010 2 πθ ϕ ϕ− = < < cosϕ a b 0cos2sin =−=⋅ θθba θθ cos2sin = 1cossin 22 =+ θθ 5 5cos,5 52sin ±=±= θθ (0, )2 πθ ∈ 5 5cos,5 52sin == θθ 20 πϕ << 20 πθ << 22 πϕθπ <−<− 10 103)(sin1)cos( 2 =−−=− ϕθϕθ cosϕ 2 2)sin(sin)cos(cos)](cos[ =−+−=−−= ϕθθϕθθϕθθ ∆ sin( ) 1C A− = 1 3 6 ∆ 2C A π− = C A Bπ+ = − 4 2 BA π= − 2sin sin( ) (cos sin )4 2 2 2 2 B B BA π= − = − 2 1 1sin (1 sin )2 3A B= − = sin 0A> 3sin 3A = sin sin AC BC B A = 36sin 3 3 21sin 3 AC ABC B • = = = sin sin( ) sin cos cos sinC A B A B A B= + = + 3 2 2 6 1 6 3 3 3 3 3 = × + × = A B C ∴ 13.（2009 安徽卷文）（本小题满分 12 分） 在 ABC 中，C-A= ， sinB= 。 （I）求 sinA 的值； (II)设 AC= ，求 ABC 的面积。 【思路】（1）依据三角函数恒等变形可得关于 的式子，这之中要运用到倍角公式； （2）应用正弦定理可得出边长，进而用面积公式可求出 . 【解析】（1）∵ ∴ ∴ ∴ 又 ∴ （2）如图，由正弦定理得 ∴ ∴ . 14.（2009 江西卷文）（本小题满分 12 分） 在△ 中， 所对的边分别为 ， ， ． （1）求 ； （2）若 ，求 , ， ． 解：（1）由 得 则有 = 得 即 . 1 1 6sin 6 3 2 3 22 2 3ABCS AC BC C∆ = • • = × × × = sin A S 2c A c A B π π− = + = −且 4 2 BA π= − 2sin sin( ) (cos sin )4 2 2 2 2 B B BA π= − = − 2 21 1 1sin (cos sin ) (1 sin )2 2 2 2 3 B BA B= − = − = sin 0A > 3cos 3A = sin sin AC BCBC B A = = 36sin 3 3 21sin 3 AC ABC B = = = ⋅⋅ sin sin( ) sin cos cos sin 3 2 2 1 6 3 3 3 3 C A B A B A B= + = + = × + × = ⋅又 1 1 6sin 6 3 2 3 22 2 3S ABC AC BC C= = × × × =⋅ ⋅ ABC , ,A B C , ,a b c 6A π= (1 3) 2c b+ = C 1 3CB CA⋅ = +  a b c (1 3) 2c b+ = 1 3 sin 2 2 sin b B c C = + = 5 5sin( ) sin cos cos sin6 6 6 sin sin C C C C C π π ππ − − − = 1 3 1 3cot2 2 2 2C + = + cot 1C = 4C π= （2） 由 推出 ；而 , 即得 , 则有 解得 15.（2009 江西卷理）（本小题满分 12 分） △ 中， 所对的边分别为 ， , . （1）求 ； （2）若 ,求 . 解：(1) 因为 ，即 ， 所以 ， 即 ， 得 . 所以 ,或 (不成立). 即 , 得 ，所以. 又因为 ，则 ，或 （舍去） 得 (2) ， 又 , 即 ， 得 16.（2009 天津卷文）（本小题满分 12 分） 在 中， （Ⅰ）求 AB 的值。 （Ⅱ）求 的值。 1 3CB CA⋅ = +  cos 1 3ab C = + 4C π= 2 1 32 ab = + 2 1 32 (1 3) 2 sin sin ab c b a c A C  = +  + =   =  2 1 3 2 a b c  =  = +  = ABC , ,A B C , ,a b c sin sintan cos cos A BC A B += + sin( ) cosB A C− = ,A C 3 3ABCS∆ = + ,a c sin sintan cos cos A BC A B += + sin sin sin cos cos cos C A B C A B += + sin cos sin cos cos sin cos sinC A C B C A C B+ = + sin cos cos sin cos sin sin cosC A C A C B C B− = − sin( ) sin( )C A B C− = − C A B C− = − ( )C A B Cπ− = − − 2C A B= + 3C π= 2 3B A π+ = 1sin( ) cos 2B A C− = = 6B A π− = 5 6B A π− = 5,4 12A B π π= = 1 6 2sin 3 32 8ABCS ac B ac∆ += = = + sin sin a c A C = 2 3 2 2 a c= 2 2, 2 3.a c= = ABC∆ ACACBC sin2sin,3,5 === )42sin( π−A 【答案】 【 解 析 】（ 1 ） 解 ： 在 中 ， 根 据 正 弦 定 理 ， ， 于 是 （2）解：在 中，根据余弦定理，得 于是 = ， 从而 【考点定位】本题主要考查正弦定理，余弦定理同角的三角函数的关系式，二倍角的正 弦和余弦，两角差的正弦等基础知识，考查基本运算能力。 17.（2009 四川卷文）（本小题满分 12 分） 在 中 ， 为 锐 角 ， 角 所 对 的 边 分 别 为 ， 且 （I）求 的值； （II）若 ，求 的值。 【解析】（I）∵ 为锐角， ∴ ∵ ∴ …………………………………………6 分 （II）由（I）知 ，∴ 10 2 ABC∆ A BC C AB sinsin = 522sinsin === BCA BCCAB ABC∆ ACAB BCACABA • −+= 2cos 222 AA 2cos1sin −= 5 5 5 3sincos2cos,5 4cossin22sin 22 =−=== AAAAAA 10 2 4sin2cos4cos2sin)42sin( =−=− πππ AAA ABC∆ A B、 A B C、 、 a b c、 、 5 10sin ,sin5 10A B= = A B+ 2 1a b− = − a b c、 、 A B、 5 10sin ,sin5 10A B= = 2 22 5 3 10cos 1 sin ,cos 1 sin5 10A A B B= − = = − = 2 5 3 10 5 10 2cos( ) cos cos sin sin .5 10 5 10 2A B A B A B+ = − = × − × = 0 A B π< + < 4A B π+ = 3 4C π= 2sin 2C = 由 得 ，即 又∵ ∴ ∴ ∴ …………………………………………12 分 18.（2009 全国卷Ⅱ理）（本小题满分 10 分） 设 的内角 、 、 的对边长分别为 、 、 ， ， ，求 。 分 析 ： 由 ， 易 想 到 先 将 代 入 得 。 然后利用两角和与差的余弦公式 展开得 ；又由 ，利用正弦定理进行边角互化，得 ， 进而得 .故 。大部分考生做到这里忽略了检验，事实上，当 时，由 ，进而得 ，矛盾， 应舍去。 也可利用若 则 从而舍去 。不过这种方法学生不易想到。 评析：本小题考生得分易，但得满分难。 19.（2009 湖南卷文）（每小题满分 12 分） 已知向量 （Ⅰ）若 ，求 的值； （Ⅱ）若 求 的值。 解：（Ⅰ） 因为 ，所以 于是 ，故 （Ⅱ）由 知， sin sin sin a b c A B C = = 5 10 2a b c= = 2 , 5a b c b= = 2 1a b− = − 2 2 1b b− = − 1b = 2, 5a c= = ABC∆ A B C a b c 3cos( ) cos 2A C B− + = 2b ac= B 3cos( ) cos 2A C B− + = ( )B A Cπ= − + 3cos( ) cos 2A C B− + = 3cos( ) cos( ) 2A C A C− − + = 3sin sin 4A C = 2b ac= 2sin sin sinB A C= 3sin 2B = 2 3 3B π π= 或 2 3B π= 1cos cos( ) 2B A C= − + = − 3cos( ) cos( ) 2 12A C A C− = + + = > 2b ac= b a b c≤ ≤或 2 3B π= (sin ,cos 2sin ), (1,2).a bθ θ θ= − =  / /a b  tanθ | | | |,0 ,a b θ π= < <  θ / /a b  2sin cos 2sin ,θ θ θ= − 4sin cosθ θ= 1tan .4 θ = | | | |a b=  2 2sin (cos 2sin ) 5,θ θ θ+ − = 所以 从而 ，即 ， 于是 .又由 知， ， 所以 ，或 . 因此 ，或 20.（2009 福建卷理）（本小题满分 13 分） 如图，某市拟在长为 8km 的道路 OP 的一侧修建一条运动 赛道，赛道的前一部分为曲线段 OSM，该曲线段为函数 y=Asin x(A>0, >0) x [0,4]的图象，且图象的最高点为 S(3，2 )；赛道的后一部分为折线段 MNP，为保证参赛 运动员的安全，限定 MNP=120 （I）求 A , 的值和 M，P 两点间的距离； （II）应如何设计，才能使折线段赛道 MNP 最长？ 18.本小题主要考查三角函数的图象与性质、解三角形等基础知识，考查运算求解能力以及 应用数学知识分析和解决实际问题的能力，考查化归与转化思想、数形结合思想， 解法一 （Ⅰ）依题意，有 ， ，又 ， 。 当 是， 又 （Ⅱ）在△MNP 中∠MNP=120°，MP=5， 设∠PMN= ，则 0°< <60° 由正弦定理得 , 故 21 2sin 2 4sin 5.θ θ− + = 2sin 2 2(1 cos2 ) 4θ θ− + − = sin 2 cos2 1θ θ+ = − 2sin(2 )4 2 πθ + = − 0 θ π< < 924 4 4 π π πθ< + < 52 4 4 π πθ + = 72 4 4 π πθ + = 2 πθ = 3 .4 πθ = ω ω ∈ 3 ∠ o ω 2 3A = 34 T = 2T π ω= 6 πω∴ = 2 3 sin 6y x π∴ = 4x = 22 3 sin 33y π∴ = = (4,3)M∴ (8,3)p 2 24 3 5MP∴ = + = θ θ 0 0sinsin120 sin(60 ) MP NP MN θ θ = = − 10 3 sin3NP θ∴ = 010 3 sin(60 )3MN θ∴ = − 010 3 10 3 10 3 1 3sin sin(60 ) ( sin cos )3 3 3 2 3NP MN θ θ θ θ+ = + − = + 0°< <60°， 当 =30°时，折线段赛道 MNP 最长 亦即，将∠PMN 设计为 30°时，折线段道 MNP 最长 解法二： （Ⅰ）同解法一 （Ⅱ）在△MNP 中，∠MNP=120°，MP=5， 由余弦定理得 ∠MNP= 即 故 从而 ，即 当且仅当 时，折线段道 MNP 最长 注：本题第（Ⅱ）问答案及其呈现方式均不唯一，除了解法一、解法二给出的两种设计方式， 还可以设计为：① ；② ；③点 N 在线段 MP 的垂直 平分线上等 21.（2009 辽宁卷文）（本小题满分 12 分） 如图，A,B,C,D 都在同一个与水平面垂直的平面内，B，D 为两岛上的两座灯塔的塔顶。测量 船于水面 A 处测得 B 点和 D 点的仰角分别为 ， ，于水面 C 处测得 B 点和 D 点的仰角 均为 ，AC＝0.1km。试探究图中 B，D 间距离与另外哪两点距离相等，然后求 B，D 的距 离（计算结果精确到 0.01km， 1.414， 2.449） （18）解： 在 中， ＝30°， ＝60°－ ＝ 30°， 所以 CD＝AC＝0.1 又 ＝180°－60°－60°＝60°， 故 CB 是 底边 AD 的中垂线，所以 BD＝BA 5 分 在 中， ， 即 AB＝ 因此， 010 3 sin( 60 )3 θ= +  θ ∴ θ 2 2 2 cosMN NP MN NP+ −   2MP 2 2 25MN NP MN NP+ + = 2 2( ) 25 ( )2 MN NPMN NP MN NP ++ − = ≤ 23 ( ) 254 MN NP+ ≤ 10 3 3MN NP+ ≤ MN NP= 12 3 9 4 3( 2 6N + +， ） 12 3 9 4 3( 2 6N − −， ） 075 030 060 2 ≈ 6 ≈ ACD∆ DAC∠ ADC∠ DAC∠ BCD∠ CAD∆ ABC∆ ABC AC BCA AB ∠=∠ sinsin 20 623 51sin 60sin +=° °AC km33.020 623 ≈+=BD 故 B、D 的距离约为 0.33km。 12 分 22.（2009 辽宁卷理）（本小题满分 12 分） 如图，A,B,C,D 都在同一个与水平面垂直的平面内，B，D 为两岛上的两座灯塔的塔顶。测量 船于水面 A 处测得 B 点和 D 点的仰角分别为 ， ，于水面 C 处测得 B 点和 D 点的仰角 均为 ，AC=0.1km。试探究图中 B，D 间距离与另外哪两点间距离相等，然后求 B，D 的 距离（计算结果精确到 0.01km， 1.414， 2.449） (17)解: 在△ABC 中，∠DAC=30°, ∠ADC=60°－∠DAC=30, 所以 CD=AC=0.1 又∠BCD=180°－60°－60°=60°， 故 CB 是△CAD 底边 AD 的中垂线，所以 BD=BA， ……5 分 在△ABC 中， 即 AB= 因此，BD= 故 B，D 的距离约为 0.33km。 ……12 分 23.（2009 宁夏海南卷理）（本小题满分 12 分） 为了测量两山顶 M，N 间的距离，飞机沿水平方向在 A，B 两点进行测量，A，B，M，N 在 同一个铅垂平面内（如示意图），飞机能够测量的数据有俯角和 A，B 间的距离，请设计一 个方案，包括：①指出需要测量的数据（用字母表示，并在图中标出）；②用文字和公式写出 计算 M，N 间的距离的步骤。 (17) 解： 方案一：①需要测量的数据有：A 075 030 060 2 ≈ 6 ≈ , ABCsin C BCAsin ∠ = ∠ AAB , 20 623 15sin ACsin60 +=   。km33.0 20 623 ≈+ 点到 M，N 点的俯角；B 点到 M， N 的俯角 ；A，B 的距离 d （如图所示） . ……….3 分 ②第一步：计算 AM . 由正弦定理 　； 第二步：计算 AN . 由正弦定理 　； 第三步：计算 MN. 由余弦定理 . 方案二：①需要测量的数据有： A 点到 M，N 点的俯角 ， ；B 点到 M，N 点的府角 ， ；A，B 的距离 d （如 图所示）. ②第一步：计算 BM . 由正弦定理 　； 　　　第二步：计算 BN . 由正弦定理 　； 第三步：计算 MN . 由余弦定理 24.（2009 陕西卷文）（本小题满分 12 分） 已知函数 （其中 ）的周期为 ，且 图象上一个最低点为 . (Ⅰ)求 的解析式；（Ⅱ）当 ，求 的最值. 解析:（1）由最低点为 由 由点 在图像上得 即 所以 故 又 ，所以 所以 （Ⅱ）因为 所以当 时，即 x=0 时，f(x)取得最小值 1； ； 2 2,α β 2 1 2 sin sin( ) dAM α α α= + 2 2 1 sin sin( ) dAN β β β= − 2 2 1 12 cos( )MN AM AN AM AN α β= + − × − 1 α 1 β 2 α 2 β 1 1 2 sin sin( ) dBM α α α= + 1 2 1 sin sin( ) dBN β β β= − 2 2 2 22 cos( )MN BM BN BM BN β α= + − × + ( ) sin( ),f x A x x Rω ϕ= + ∈ 0, 0,0 2A πω ϕ> > < < π 2( , 2)3M π − ( )f x [0, ]12x π∈ ( )f x 2( , 2) 23M A π − =得 2 2 2T T π ππ ω π= = = =得 2( , 2)3M π − 42sin( ) 23 π ϕ+ = − 4sin( ) 13 π ϕ+ = − 4 23 2k π πϕ π+ = − 112 ( )6k k Z πϕ π= − ∈ (0, )2 πϕ ∈ 6 πϕ = ( ) 2sin(2 )6f x x π= + [0, ],2 [ , ]12 6 6 3x x π π π π∈ + ∈ 2x+ 6 6 π π= , ( )6 3 12x f x π π π= =当2x+ 即 时， 取得最大值 3 1 1,α β 25.(2009 陕西卷理)（本小题满分 12 分） 已知函数 （其中 ）的图象与 x 轴的 交点中，相邻两个交点之间的距离为 ，且图象上一个最低点为 . (Ⅰ)求 的解析式；（Ⅱ）当 ，求 的值域. 17、解（1）由最低点为 得 A=2. 由 x 轴上相邻的两个交点之间的距离为 得 = ，即 ， 由点 在图像上的 故 又 （2） 当 = ，即 时， 取得最大值 2；当 即 时， 取得最小值-1，故 的值域为[-1,2] 26.（2009 四川卷文）（本小题满分 12 分） 在 中 ， 为 锐 角 ， 角 所 对 的 边 分 别 为 ， 且 （I）求 的值； （II）若 ，求 的值。 【解析】（I）∵ 为锐角， ∴ ∵ ∴ …………………………………………6 分 ( ) sin( ),f x A x x Rω ϕ= + ∈ 0, 0,0 2A πω ϕ> > < < 2 π 2( , 2)3M π − ( )f x [ , ]12 2x π π∈ ( )f x 2( , 2)3M π − 2 π 2 T 2 π T π= 2 2 2T π πω π= = = 2( , 2)3M π − 2 42sin(2 ) 2, ) 13 3 π πϕ ϕ× + = − + = −即si n( 4 2 ,3 2k k Z π πϕ π+ = − ∈ 112 6k πϕ π∴ = − (0, ), , ( ) 2sin(2 )2 6 6f x x π π πϕ ϕ∈ ∴ = = +故 7[ , ], 2 [ , ]12 2 6 3 6x x π π π π π∈ ∴ + ∈ 2 6x π+ 2 π 6x π= ( )f x 72 6 6x π π+ = 2x π= ( )f x ( )f x ABC∆ A B、 A B C、 、 a b c、 、 5 10sin ,sin5 10A B= = A B+ 2 1a b− = − a b c、 、 A B、 5 10sin ,sin5 10A B= = 2 22 5 3 10cos 1 sin ,cos 1 sin5 10A A B B= − = = − = 2 5 3 10 5 10 2cos( ) cos cos sin sin .5 10 5 10 2A B A B A B+ = − = × − × = 0 A B π< + < 4A B π+ = （II）由（I）知 ，∴ 由 得 ，即 又∵ ∴ ∴ ∴ …………………………………………12 分 27.（2009 湖北卷文）（本小题满分 12 分） 在锐角△ABC 中，a、b、c 分别为角 A、B、C 所对的边，且 (Ⅰ)确定角 C 的大小： （Ⅱ）若 c＝ ,且△ABC 的面积为 ,求 a＋b 的值。 解（1）由 及正弦定理得， 是锐角三角形， （2）解法 1： 由面积公式得 由余弦定理得 由②变形得 解法 2：前同解法 1，联立①、②得 3 4C π= 2sin 2C = sin sin sin a b c A B C = = 5 10 2a b c= = 2 , 5a b c b= = 2 1a b− = − 2 2 1b b− = − 1b = 2, 5a c= = Aca sin23 = 7 2 33 3 2 sina c A= 2sin sin sin3 a A A c C = = 3sin 0, sin 2A C≠ ∴ = ABC∆ 3C π∴ = 7, .3c C π= = 1 3 3sin , 62 3 2ab ab π = =即 ① 2 2 2 22 cos 7, 73a b ab a b ab π+ − = + − =即 ② 25, 5a b= + =2（a+b) 故 2 2 2 27 6 6 a b ab a b ab ab  + − = +⇔ = =  ＝１３ 消去 b 并整理得 解得 所以 故 28.（2009 宁夏海南卷文）（本小题满分 12 分） 如图，为了解某海域海底构造，在海平面内一条直线上的 A，B，C 三点 进行测量，已知 ， ，于 A 处测得水深 ， 于 B 处测得水深 ，于 C 处测得水深 ，求∠DEF 的 余弦值。 (17) 解： 作 交 BE 于 N，交 CF 于 M． ， ， ．　．．．．．．6 分 在 中，由余弦定理， . ．．．．．．12 分 29.(2009 湖南卷理)（本小题满分 12 分） 在 ，已知 ，求角 A，B，C 的大小。 解：设 由 得 ，所以 又 因此 由 得 ，于是 所以 ， ，因此 4 213 36 0a a− + = 2 24 9a a= =或 2 3 3 2 a a b b = =   = =  或 5a b+ = 50AB m= 120BC m= 80AD m= 200BE m= 110CF m= //DM AC 2 2 2 230 170 10 198DF MF DM= + = + = 2 2 2 250 120 130DE DN EN= + = + = 2 2 2 2( ) 90 120 150EF BE FC BC= − + = + = DEF∆ 2 2 2 2 2 2130 150 10 298 16cos 2 2 130 150 65 DE EF DFDEF DE EF + − + − ×∠ = = =× × × ABC∆ 22 3 3AB AC AB AC BC⋅ = ⋅ =    , ,BC a AC b AB c= = = 2 3AB AC AB AC⋅ = ⋅    2 cos 3bc A bc= 3cos 2A = (0, ),A π∈ 6A π= 23 3AB AC BC⋅ =  23bc a= 2 3sin sin 3sin 4C B A⋅ = − 5 3sin sin( )6 4C C π⋅ − = 1 3 3sin ( cos sin )2 2 4C C C⋅ + = ，既 由 A= 知 ，所以 ， ，从而 或 ，既 或 故 或 。 30.（2009 天津卷理）（本小题满分 12 分） 在⊿ABC 中，BC= ，AC=3，sinC=2sinA (I) 求 AB 的值： (II) 求 sin 的值 本小题主要考查正弦定理、余弦定理、同角三角函数的基本关系、二倍角的正弦与余弦、两 角差的正弦等基础知识，考查基本运算能力。满分 12 分。 （Ⅰ）解：在△ABC 中，根据正弦定理， 于是 AB= （Ⅱ）解：在△ABC 中，根据余弦定理，得 cosA= 于是 sinA= 从而 sin2A=2sinAcosA= ,cos2A=cos2A-sin2A= 所以 sin(2A- )=sin2Acos -cos2Asin = 31.（2009 四川卷理）（本小题满分 12 分） 在 中 ， 为 锐 角 ， 角 所 对 应 的 边 分 别 为 ， 且 （I）求 的值； （II）若 ，求 的值。 本小题主要考查同角三角函数间的关系，两角和差的三角函数、二倍角公式、正弦定理等 基础知识及基本运算能力。 解：（Ⅰ） 、 为锐角， ， 22sin cos 2 3sin 3,sin 2 3 cos2 0C C C C C⋅ + = − = sin(2 ) 03C π− = 6 π 50 6C π< < 3 π− 42 3 3C π π− < 2 0,3C π− = 2 ,3C π π− = ,6C π= 2 ,3C π= 2, , ,6 3 6A B C π π π= = = 2, ,6 6 3A B C π π π= = = 5 2 4A π −   A BC C AB sinsin = 522sin sin == BCBCA C 5 52 2 222 =• −+ ACAB BDACAB 5 5cos1 2 =− A 5 4 5 3 4 π 4 π 4 π 10 2 ABC ,A B , ,A B C , ,a b c 3 10cos2 ,sin5 10A B= = A B+ 2 1a b+ = − , ,a b c A B 10sin 10B = 2 3 10cos 1 sin 10B b∴ = − = 又 ， ， ， …………………………………………6 分 （Ⅱ）由（Ⅰ）知 , . 由正弦定理 得 ，即 ， ， ， ……………………………………12 分 32.（2009 福建卷文）（本小题满分 12 分） 已知函数 其中 ， （I）若 求 的值； （Ⅱ）在（I）的条件下，若函数 的图像的相邻两条对称轴之间的距离等于 ，求 函数 的解析式；并求最小正实数 ，使得函数 的图像象左平移 个单位所对应 的函数是偶函数。 解法一： （I）由 得 即 又 （Ⅱ）由（I）得， 依题意， 2 3cos2 1 2sin 5A A= − = 5sin 5A∴ = 2 2 5cos 1 sin 5A A= − = 2 5 3 10 5 10 2cos( ) cos cos sin sin 5 10 5 10 2A B A B A B∴ + = − = × − × = 0 A B π< + < 4A B π∴ + = 3 4C π= 2sin 2C∴ = sin sin sin a b c A B C = = 5 10 2a b c= = 2a b= 5c b= 2 1a b− = − 2 2 1b b∴ − = − 1b∴ = 2, 5a c∴ = = ( ) sin( ),f x xω ϕ= + 0ω > | | 2 πϕ < cos cos, sin sin 0,4 4 π πϕ ϕ3− = ϕ ( )f x 3 π ( )f x m ( )f x m 3cos cos sin sin 04 4 π πϕ ϕ− = cos cos sin sin 04 4 π πϕ ϕ− = cos( ) 04 π ϕ+ = | | ,2 4 π πϕ ϕ< ∴ = ( ) sin( )4f x x πω= + 2 3 T π= 又 故 函数 的图像向左平移 个单位后所对应的函数为 是偶函数当且仅当 即 从而，最小正实数 解法二： （I）同解法一 （Ⅱ）由（I）得， 依题意， 又 ，故 函数 的图像向左平移 个单位后所对应的函数为 是偶函数当且仅当 对 恒成立 亦即 对 恒成立。 即 对 恒成立。 故 从而，最小正实数 33.（2009 重庆卷理）（本小题满分 13 分，（Ⅰ）小问 7 分，（Ⅱ）小问 6 分．） 2 ,T π ω= 3, ( ) sin(3 )4f x x πω = ∴ = + ( )f x m ( ) sin 3( ) 4g x x m π = + +   ( )g x 3 ( )4 2m k k Z π ππ+ = + ∈ ( )3 12 km k Z π π= + ∈ 12m π= ( ) sin( )4f x x πω= + 2 3 T π= 2T π ω= 3, ( ) sin(3 )4f x x πω = ∴ = + ( )f x m ( ) sin 3( ) 4g x x m π = + +   ( )g x ( ) ( )g x g x− = x R∈ sin( 3 3 ) sin(3 3 )4 4x m x m π π− + + = + + x R∈ sin( 3 )cos(3 ) cos( 3 )sin(3 )4 4x m x m π π∴ − + + − + sin3 cos(3 ) cos3 sin(3 )4 4x m x m π π= + + + 2sin3 cos(3 ) 04x m π+ = x R∈ cos(3 ) 04m π∴ + = 3 ( )4 2m k k Z π ππ+ = + ∈ ( )3 12 km k Z π π∴ = + ∈ 12m π= 设函数 ． （Ⅰ）求 的最小正周期． （Ⅱ）若函数 与 的图像关于直线 对称，求当 时 的最大值． 解：（Ⅰ） = = = 故 的最小正周期为 T = =8 (Ⅱ)解法一： 在 的图象上任取一点 ，它关于 的对称点 . 　　由题设条件，点 在 的图象上，从而 　　　　　　　　　 = = 当 时， ，因此 在区间 上的最大值为 　　　 　　解法二： 因区间 关于 x = 1 的对称区间为 ，且 与 的图象关于 　　x = 1 对称，故 在 上的最大值为 在 上的最大值 　　由（Ⅰ）知 ＝ 当 时， 2( ) sin( ) 2cos 14 6 8 x xf x π π π= − − + ( )f x ( )y g x= ( )y f x= 1x = 4[0, ]3x∈ ( )y g x= ( )f x sin cos cos sin cos4 6 4 6 4x x x π π π π π− − 3 3sin cos2 4 2 4x x π π− 3sin( )4 3x π π− ( )f x 2 4 π π ( )y g x= ( , ( ))x g x 1x = (2 , ( ))x g x− (2 , ( ))x g x− ( )y f x= ( ) (2 ) 3sin[ (2 ) ]4 3g x f x x π π= − = − − 3sin[ ]2 4 3x π π π− − 3 cos( )4 3x π π+ 30 4x≤ ≤ 2 3 4 3 3x π π π π≤ + ≤ ( )y g x= 4[0, ]3 max 33 cos 3 2g π= = 4[0, ]3 2[ ,2]3 ( )y g x= ( )y f x= ( )y g x= 4[0, ]3 ( )y f x= 2[ ,2]3 ( )f x 3sin( )4 3x π π− 2 23 x≤ ≤ 6 4 3 6 π π π π− ≤ − ≤ 　　　因此 在 上的最大值为 　　　　　　　 . 34.（2009 重庆卷文）（本小题满分 13 分，（Ⅰ）小问 7 分，（Ⅱ）小问 6 分．） 设函数 的最小正周期为 ． （Ⅰ）求 的最小正周期． （Ⅱ）若函数 的图像是由 的图像向右平移 个单位长度得到，求 的单调增区间． 解：（Ⅰ） 依题意得 ，故 的最小正周期为 . （Ⅱ）依题意得: 由 解得 故 的单调增区间为: 35.（2009 上海卷文）（本题满分 14 分）本题共有 2 个小题，第 1 小题满分 6 分，第 2 小题 满分 8 分 . 已知ΔABC 的角 A、B、C 所对的边分别是 a、b、c，设向量 ， 　　 ， . （1） 若 // ，求证：ΔABC 为等腰三角形； （2） 若 ⊥ ，边长 c = 2，角 C = ，求ΔABC 的面积 . 证明：（1） 即 ，其中 R 是三角形 ABC 外接圆半径， ( )y g x= 4[0, ]3 max 33sin 6 2g π= = 2 2( ) (sin cos ) 2cos ( 0)f x x x xω ω ω ω= + + > 2 3 π ω ( )y g x= ( )y f x= 2 π ( )y g x= 2 2 2 2( ) (sin cos ) 2cos sin cos sin 2 1 2cos2f x x x x x x x xω ω ω ω ω ω ω= + + = + + + + sin 2 cos2 2 2 sin(2 ) 24x x x πω ω ω= + + = + + 2 2 2 3 π π ω = ω 3 2 5( ) 2 sin 3( ) 2 2 sin(3 ) 22 4 4g x x x π π π = − + + = − +   52 3 2 ( )2 4 2k x k k Z π π ππ π− − + ∈≤ ≤ 2 2 7 ( )3 4 3 12k x k k Z π ππ π+ + ∈≤ ≤ ( )y g x= 2 2 7[ , ] ( )3 4 3 12k k k Z π ππ π+ + ∈ ( , )m a b= (sin ,sin )n B A= ( 2, 2)p b a= − − m n m p 3 π // , sin sin ,m n a A b B∴ =   2 2 a ba bR R ⋅ = ⋅ a b= 为等腰三角形 解（2）由题意可知 由余弦定理可知， ABC∴∆ // 0, ( 2) ( 2) 0m p a b b a= − + − =  即 a b ab∴ + = 2 2 24 ( ) 3a b ab a b ab= + − = + − 2( ) 3 4 0ab ab− − =即 4( 1)ab ab∴ = = −舍去 1 1sin 4 sin 32 2 3S ab C π∴ = = ⋅ ⋅ =