高考数学专题复习专题六平面向量教案文 7页

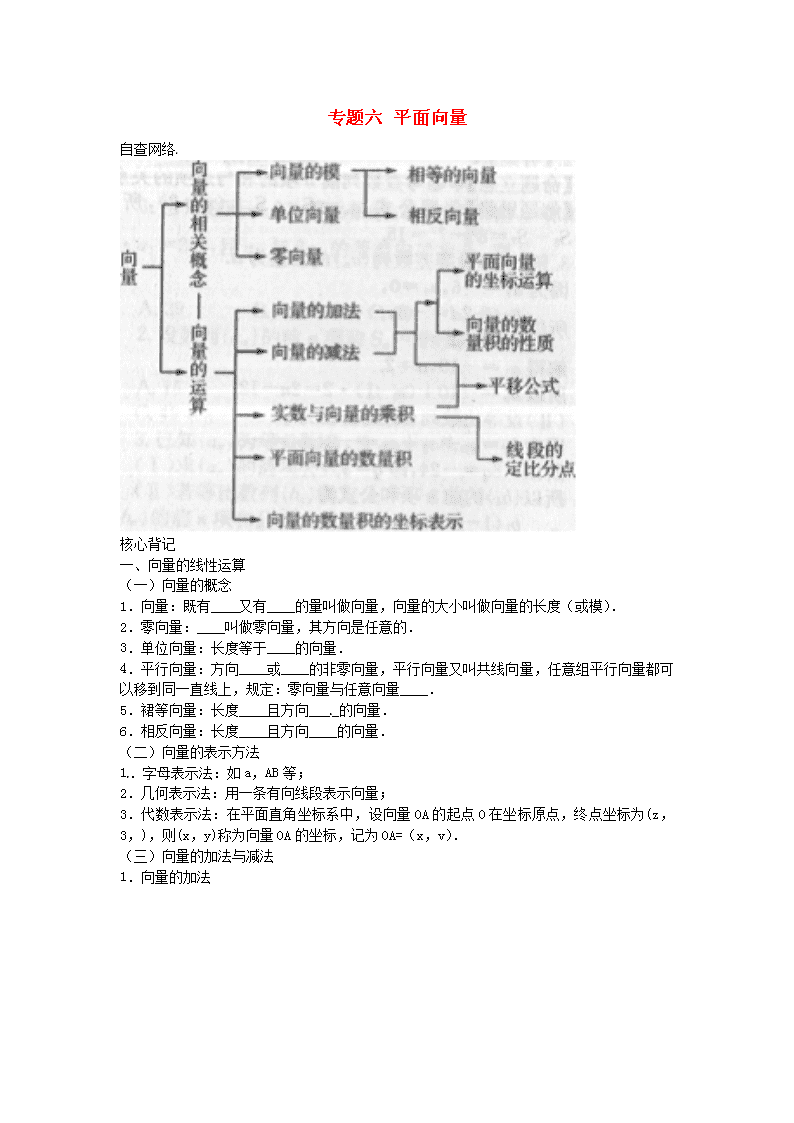
专题六 平面向量 自查网络 核心背记  一、向量的线性运算  （一）向量的概念  1．向量：既有____又有____的量叫做向量，向量的大小叫做向量的长度（或模）．  2．零向量：____叫做零向量，其方向是任意的．  3．单位向量：长度等于____的向量．  4．平行向量：方向____或____的非零向量，平行向量又叫共线向量，任意组平行向量都可以移到同一直线上，规定：零向量与任意向量____． 5．裙等向量：长度____且方向____的向量． 6．相反向量：长度____且方向____的向量． （二）向量的表示方法 1．字母表示法：如a，AB等；     2．几何表示法：用一条有向线段表示向量； 3．代数表示法：在平面直角坐标系中，设向量OA的起点0在坐标原点，终点坐标为(z，3，)，则(x，y)称为向量OA的坐标，记为OA=（x，v）． （三）向量的加法与减法 1．向量的加法  ‎ ‎ 则、平行四边形法则，有时也用向量减法的定义． (2)证明线段的垂直问题，如证明四边形是矩形、正  形，判断两直线（或线段）是否垂直等，常运用向量垂直  条件albgi____． (3)求与夹角有关的问题，往往利用向量的夹角公式  如判断三角形的形状，求三角形的面积等． (4)向量的坐标法，对于有些平面几何问题，如长方  形、正方形、直角三角形等，建立直角坐标系，把向量用坐  标表示，通过代数运算解决几何问题． (5)用向量方法解决平面几何问题的步骤      首先，建立平面几何与向量的联系，用向量表示问题  中涉及的几何元素，将平面几何问题转化为向量问题；其  次，通过向量运算，研究几何元素_之间的关系；最后，把运  算结果“翻译”成几何关系． 2.向量在解析几何中的应用( 1)直线的倾斜角、斜率与平行于该直线的向量之间    的关系：设直线Z的倾斜角为口，斜率为七，向量口一（口，，a。）  平行于2，则k2‎ ‎ tana2导；如果已知直线的斜率k-署，则  向量———一与向量（1，矗）一定都与Z平行． (2)与a= (ai，口2)平行且过P(xo，yo)的直线方程  ~J-;d点P(.ro，yo)且与向量a-（口，，口：）垂直的  直线方程为____．.． 向量在物理中的应用 (1)力向量：力向量是具有大小、方向和作用点的向  量，它与前面学习的自由向量不同，但力是具有大小和方  向的量，在不考虑作用点的情况下，可用向量求和的平行  四边形法则求两个力的合力． 2)速度向量：是具有大小和方向的向量，可用平行四边形法则求两个速度的合速度． (3)用向量方法解决物理问题的步骤：一是把物理问题中的相关量用向量表示； 二是转化为向量问题的模型，通过向量运算使问题得以解决； 三是将结果还原为物理问题． ‎ 参考答案 一、（一）1．大小方向 2．长度为零的向量 3.1个单位长度 4．相同相反平行 5．相等相同 6．相等相反 （四）1．相同相反0 （五）有且只有一个实数λ．使得b=λa 规律探究 1．向量是既有大小又有方向的量，从其定义可以看出向量既有代数特征又有几何特征，因此借助于向量，我们可以将某些代数问题转化为几何问题，又可将几何问题转化为代数问题，故向量能起到数形结合的桥梁作用（本节重点突出了数形结合的思想）．在一个复杂的几何图形中恰当地选择两个不共线向量来表示其他向量，然后进行运算是解决向量问题的基本方法． 2．对共线向量、相等向量的概念能否正确理解和牢固掌握很重要，它关系到我们今后在解决相关问题时能否灵活应用的问题． 3．两个向量的长度可以比较大小，但方向没有大小，因此“大于”和“小于”的概念对于向量无意义，如“a>b”没有意义，而laj>lbl则有意义． 4．两个向量的加法有三角形法则和平行四边形法则，向量的减法是向量加法的逆运算． 5．I lal - lblI≤l口±bl≤la[+lbl，探讨该式中等号成立的条件 ‎，可以解决许多相关的问题． 6．要区别两向量平行和两直线平行．两向量平行，即两向量共线，这和两直线平行不同，利用向量平行条件证明两条直线平行往往是通过“点的坐标”来实现的，利用向量运算可以解决平面几何问题，如：三点共线、线共点、两线平行．  7．平面向量的坐标运算法则是运算的关键，平面向量的坐标运算可将几何问题转化为代数问题，运用它可以解决平面几何、解析几何中的一些问题．   9．向量作为一种既有大小又有方向的量，既具有形的特性，又具有数的特性，因而成为联系数和形的有力纽带．由于向量具有数的特性，因而向量容易成为初等数学中的函数、三角、数列、不等式等许多重要内容的交汇点，而且我们也可以通过构造向量来处理许多代数问题，另外，平面向量在平面几何、解析几何中的应用也十分重要，平面向量与几何问题的综合及应用通常涉及长度、角度、平行、垂直、共线等问题的处理，目标是将几何问题坐标化、符号化、数量化，从而将推理转化为运算．一般研究夹角问题总是从数量积人手，研究长度则从模的运算性质入手，而研究共线、共点问题则多从实数与向量的积人手， 实际应用 ‎