空间几何体的表面积和体积最新高考试题汇编 32页

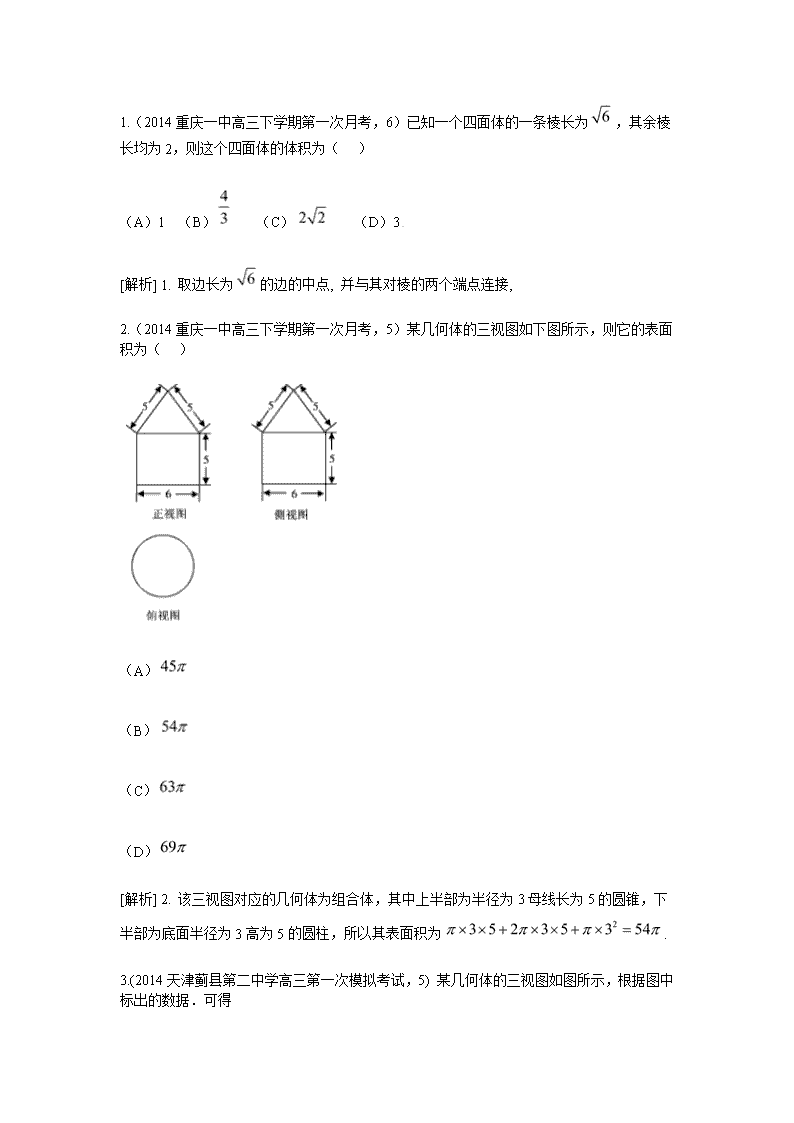
‎1.（2014重庆一中高三下学期第一次月考，6）已知一个四面体的一条棱长为，其余棱长均为2，则这个四面体的体积为（    ）‎ ‎（A）1    （B）     （C）     （D）3‎ ‎[解析] 1.  取边长为的边的中点, 并与其对棱的两个端点连接,‎ ‎2.（2014重庆一中高三下学期第一次月考，5）某几何体的三视图如下图所示，则它的表面积为（    ）‎ ‎（A）‎ ‎（B）‎ ‎（C）‎ ‎（D）‎ ‎[解析] 2.  该三视图对应的几何体为组合体，其中上半部为半径为3母线长为5的圆锥，下半部为底面半径为3高为5的圆柱，所以其表面积为.‎ ‎3.(2014天津蓟县第二中学高三第一次模拟考试，5) 某几何体的三视图如图所示，根据图中标出的数据．可得 这个几何体的表面积为(      )‎ A.     ‎ B. ‎ C.         ‎ D. 12‎ ‎[解析] 3.  从三视图中可以看出该几何体是正四棱锥，且其斜高为底面是边长为2的正方形，故其表面积为.‎ ‎4. (2014山西忻州一中、康杰中学、临汾一中、长治二中四校高三第三次联考，11) 三棱锥P—ABC的四个顶点均在同一球面上，其中△ABC是正三角形，PA⊥平面ABC，‎ PA＝2AB＝6，则该球的体积为(　)‎ ‎[解析] 4.  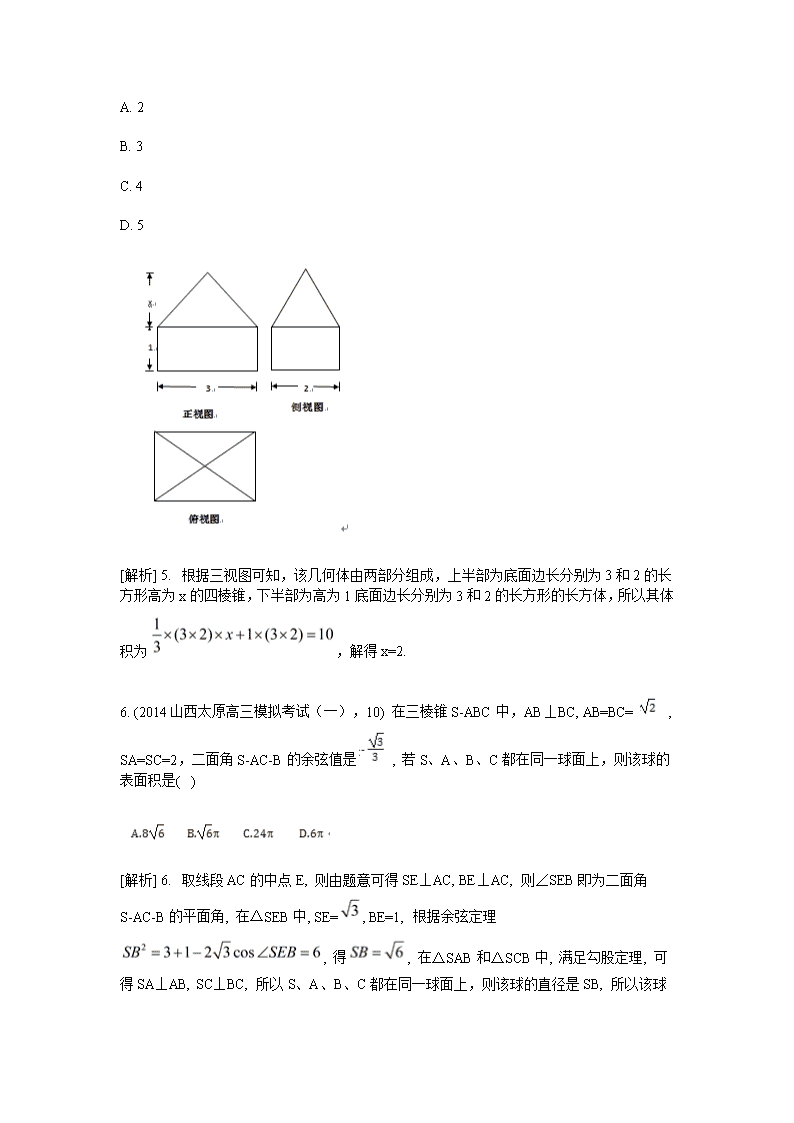三棱锥P－ABC的外接球与高为6底面边长为3的正三棱柱的外接球相同，即可把三棱锥P－ABC补成高为6底面边长为3的正三棱柱，由此可得球心O到底面ABC的距离为3，设底面ABC的外接圆圆心为O1, 连接OA, O1A、OO1, 则O1A =, OO1=3，所以OA2=O1A2+=，所以该求的体积为.‎ ‎5. (2014山西忻州一中、康杰中学、临汾一中、长治二中四校高三第三次联考，3) 下图是一个体积为10的空间几何体的三视图，则图中x的值为(  ) ‎ A. 2‎ B. 3　　　　　　      ‎ C. 4　　        ‎ D. 5‎ ‎[解析] 5.  根据三视图可知，该几何体由两部分组成，上半部为底面边长分别为3和2的长方形高为x的四棱锥，下半部为高为1底面边长分别为3和2的长方形的长方体，所以其体积为，解得x=2.‎ ‎6. (2014山西太原高三模拟考试（一），10) 在三棱锥S-ABC中，AB⊥BC, AB=BC= , SA=SC=2，二面角S-AC-B的余弦值是 , 若S、A、B、C都在同一球面上，则该球的表面积是(   ) ‎ ‎[解析] 6.  取线段AC的中点E, 则由题意可得SE⊥AC, BE⊥AC, 则∠SEB即为二面角S-AC-B的平面角, 在△SEB中, SE=, BE=1, 根据余弦定理, 得, 在△SAB和△SCB中, 满足勾股定理, 可得SA⊥AB, SC⊥BC, 所以S、A、B、C都在同一球面上，则该球的直径是SB, 所以该球 的表面积为.‎ ‎7. (2014山西太原高三模拟考试（一），8) 一个几何体的三视图如图所示（单位：cm），则该几何体的体积为(   ) ‎ A. （32+ ) ㎝3‎ B. （32+ ) ㎝3‎ C. （41+ ) ㎝3‎ D. （41+ ) ㎝3‎ ‎[解析] 7.  该三视图对应的几何体为由上中下三部分构成的组合体，其中上半部是长宽高分别为3、3、1的长方体；中半部为底面直径为1高为1的圆柱；下半部为长宽高分别为4、4、2的长方体，其体积为.‎ ‎8.(2014安徽合肥高三第二次质量检测，3) 某空间几何体的三视图如图所示，则该几何体的体积为（   ）‎ ‎  A.            ‎ B.            ‎ C. ‎ D. [‎ ‎   ‎ ‎[解析] 8.  由三视图知，原几何体是一个三棱柱，底面是等腰直角三角形，且腰长为2，‎ 所以该三棱柱的体积.‎ ‎9. (2014重庆杨家坪中学高三下学期第一次月考，6) 已知某几何体的三视图如图所示，若该几何体的体积为24，则该几何体的底面积是（  ）‎ A. 6‎ B. 12‎ C. 18‎ D. 24‎ ‎[解析] 9.  根据三视图可知，该几何体是一个有一条侧棱垂直于底面的四棱锥，该四棱锥的高为4，因为体积 为24，所以底面积.‎ ‎10. (2014河北石家庄高中毕业班复习教学质量检测（二），8) 点,  ，，在同一 个球的球面上，，, 若四面体体积的最大值为 , 则该球的表面积为(    ) ‎ ‎[解析] 10.  如图，当平面时，四面体体积的最大. 此时，，所以，设球半径为R，则,‎ 即，从而，故.‎ ‎11. (2014湖北黄冈高三4月模拟考试，6) 一个几何体的三视图如图所示，其中正视图是正三角形，则几何体的外接球的表面积为（    ）‎ ‎    A. ‎ B.          ‎ C.           ‎ D.  ‎ ‎[解析] 11.原几何体如图中三棱锥，由已知正视图、侧视图和俯视图均是三角形，可知该几何体有一个侧面垂直于底面，高为，底面是一个等腰直角三角形，则这个几何体的外接球的球心在高线上，且是等边三角形的中心，[学|科|网Z|X|X|K]‎ 所以这个几何体的外接球的半径为，‎ 所以这个几何体的外接球的表面积为.‎ ‎12. (2014河北唐山高三第一次模拟考试，9) 正三棱锥的高和底面边长都等于6，则其外接球的表面积为（    ）‎ ‎    A.          ‎ B.       ‎ C.          ‎ D. ‎ ‎[解析] 12.  设球半径为， 如图所示，可得，解得，所以表面积为.‎ ‎13. (2014河北唐山高三第一次模拟考试，7) 某几何体的三视图如图所示，则该几何体的体积为（    ）‎ A. 6        ‎ B. 2      ‎ C. 3          ‎ D.‎ ‎[解析] 13.  由三视图知，原几何体的体积为.‎ ‎14. (2014贵州贵阳高三适应性监测考试, 5) 下图是一个几何体的三视图，则该几何体的体积等于（    ）‎ ‎[]‎ ‎[解析] 14.该几何体是一三棱柱，qi 其体积为=4.‎ ‎15. (2014黑龙江哈尔滨第三中学第一次高考模拟考试，8) 如图所示，是一个空间几何体的三视图，且这个空间几何体的所有顶点都在同一个球面上，则这个球的表面积是（    ）‎ A.   ‎ B.  ‎ C.    ‎ D. ‎ ‎[解析] 15.  由三视图知，原几何体是一个三棱柱，其底边为边长为2的等边三角形，高为2，‎ 所以球心在三棱柱上下两底面的中心的连线的中点，‎ 球的半径为，球的表面积为.‎ ‎16.（2014山东潍坊高三3月模拟考试数学（理）试题，7）三棱锥S-ABC的所有顶点都在球O的表面上，SA平面ABC，ABBC，又SA=AB= BC=1，则球O的表面积为(  )‎ ‎  (A)   　(B) ‎ ‎  (C)  3  　 (D) 12‎ ‎[解析] 16.  三棱锥S－ABC的外接球与高为1底面边长为1等腰直角三角形的直三棱柱的外接球相同，即可把三棱锥P－ABC补成高为1底面边长为1等腰直角三角形的直三棱柱，由此可得球心O到底面ABC的距离为，设底面ABC的外接圆圆心为O1, 连接OA, O1A、OO1, 则O1A =, OO1=，所以OA2=O1A2+=，所以该求的体积为.‎ ‎17.（2014吉林实验中学高三年级第一次模拟，8）若某棱锥的三视图(单位：cm) 如图所示，‎ 则该棱锥的体积等于（    ）‎ A．10 cm3　　     B．20 cm3‎ C．30 cm3　　     D．40 cm3            ‎ ‎[解析] 17.  根据三视图可知，该几何体为如下图所示的四棱锥，其中PA⊥PB，底面ABCD为矩形且与侧面PAB垂直，过点P作线段AB的垂线，则该垂线即为四棱锥的高，其长度为cm，而矩形ABCD的边长AD=5，AB=5，所以其体积为 cm3.‎ ‎18.（2014湖北八校高三第二次联考数学（理）试题，4）已知某几何体的三视图（单位：cm）如图所示，则该几何体的体积是（  ）‎ ‎　A．48cm3           B．98cm3          C．88cm3           D．78cm3‎ ‎[解析] 18.  该三视图对应的几何体为长、宽、高分别为6 cm、3 cm、6 cm的长方体截去一个三棱锥后所得的几何体，其体积为6×3×6－98 cm3.‎ ‎19.(2014河南豫东豫北十所名校高中毕业班阶段性测试（四）数学（理）试题, 11) ‎ 如图所示，棱长为6的正方体无论从哪一个面看，都有两个直通的边长为l的正方形孔，则这个有孔正方体的表面积（含孔内各面）是(  )‎ ‎ ( A) 222　　(B) 258          　(C) 312           　(D) 324‎ ‎[解析] 19.  表面积等于正方体的表面积减去12个表面上的小正方形面积，加上6个棱柱的侧面积，减去6个通道的6个小正方体的表面积．则S=6×36-12+6×4×6-6×6=312．故选C．‎ ‎20.(2014河南豫东豫北十所名校高中毕业班阶段性测试（四）数学（理）试题, 4) 某几何体的三视图如图所示，其中正视图与侧视图均为矩形，俯视图上半部分为半，圆，则该几何体的体积为(  )‎ ‎     (A)           (B)            (C)        (D) ‎ ‎[解析] 20.  根据三视图可知，该几何题是由半圆柱和直三棱柱构成的组合体，其中半圆柱的底面半径为1，高为2；直三棱柱的底面是腰长为的等腰直角三角形，故该几何体的体积为.‎ ‎21.(2014吉林省长春市高中毕业班第二次调研测试，9) 某几何体的三视图如图所示，则它的表面积为（  ）‎ A．　　　　  B．‎ C．　　             D．‎ ‎[解析] 21.  由几何体的三视图可知，该几何体是一个沿旋转轴作截面，截取的半个圆锥，底面半径是1，高是2，所以母线长为，所以其表面积为底面半圆面积和圆锥的侧面积的一半以及截面三角形的面积的和，即，故选.‎ ‎22.(2014湖北武汉高三2月调研测试，8) 如图，在长方体ABCD-A1B1C1D1中，E，H分别是棱A1B1，D1C1上的点（点E与B1不重合），且EH∥A1D1，过EH的平面与棱BB1，CC1相交，交点分别为F，G．设AB＝2AA1＝2a．在长方体ABCD-A1B1C1D1内随机选取一点，记该点取自于几何体A1ABFE-D1DCGH内的概率为P，当点E，F分别在棱A1B1，BB1上运动且满足EF＝a时，则P的最小值为 ‎[解析] 22.  根据几何概型，‎ ‎=== ，‎ 其中“＝” 当且仅当时成立. 故选D.‎ ‎23.  (2014吉林高中毕业班上学期期末复习检测, 7) 某几何体的三视图（如图），则该几何体的体积是（    ）‎ A.          ‎ B.  ‎ C.           ‎ D.  ‎ ‎[解析] 23.   由三视图知，原几何体是由一个半圆柱与一个半圆锥构成，其体积为.‎ ‎24. (2014河南郑州高中毕业班第一次质量预测, 4) 如图，某几何体的正视图和俯视图都是矩形，侧视图是平行四边形，则该几何体的表面积为（    ）‎ A.        ‎ B.       ‎ C.        ‎ D. ‎ ‎[解析] 24.由已知，元几何体为四棱柱，其底面边长为，侧视图的高为，‎ 底面积为，又因为棱柱的高为3，侧面积为，‎ 故原几何体的表面积为.‎ ‎25. (2014河北衡水中学高三上学期第五次调研考试, 3) 一个几何体按比例绘制的三视图如图所示（单位：）, 则该几何体的体积为（　　）．　　‎ ‎[学#科#网]‎ A．　　B. 　　C．D. ‎ ‎[解析] 25.由三视图可知，该几何体是由三个棱长为1的正方体加半个正方体构成，所以体积为 ‎26.(2014成都高中毕业班第一次诊断性检测，8) 一个长方体被一个平面截去一部分后所剩几何体的三视图如下图所示（单位：cm) ，则该几何体的体积为（    ）‎ ‎(A) 120       (B) 80    (C) 100　　　 (D) 60 ‎ ‎[解析] 26.画出直观图可知，原几何体的体积.‎ ‎27. (2014北京东城高三12月教学质量调研) 一个空间几何体的三视图如图所示，则该几何体的体积为（    ）‎ ‎（A）　　　　（B）　　　　（C）　　　　（D）‎ ‎[解析] 27.  原几何体是由一个圆柱与一个圆锥构成，其体积为.‎ ‎28.13．(2014天津蓟县邦均中学高三第一次模拟考试，13) 如果一个几何体的三视图如图所示(单位长度: cm),  则此几何体的表面积是          。‎ ‎[解析] 28.  该三视图对应的几何体为组合体, 其中上半部为底面边长为2, 斜高为的正四棱锥, 下半部分是边长为2的正方体, 所以其表面积为.‎ ‎29. (2014福州高中毕业班质量检测, 14) 已知某几何体的三视图(单位: cm) 如图所示, 则该几何体的表面积为        . ‎ ‎[解析] 29.  由三视图知，原几何体是一个棱长为2的正方体削去一个三棱锥后剩下的一个七面体 ‎，截面三角形为边长为的等边三角形，截面的面积为，‎ 所以几何体的表面积为.‎ ‎30. (2014贵州贵阳高三适应性监测考试, 15) 已知四棱锥的顶点在球心，底面正方形的四个顶点在球面上，且四棱锥的体积为，，则球的体积为　　　　　. ‎ ‎[解析] 30.因为底面正方形的四个顶点在球面上，所以四个顶点在一个小圆面上，且与是小圆直径. 所以，，又，从而由+得：，故.‎ ‎31.（2014山东潍坊高三3月模拟考试数学（理）试题，11）已知某几何体的三视图如图所示，则该几何体的体积为       ‎ ‎[解析] 31.  根据三视图可知，该几何体是底面为以2和3为直角边的直角三角形高为4的三棱柱，其体积为.‎ ‎32. (2014广西桂林中学高三2月月考，16) 正三角形的边长为2，将它沿高翻折，使点与点间的距离为1，此时四面体外接球表面积为   ▲    ．‎ ‎[解析] 32.  根据题意知，三棱锥的三条侧棱，，底面是正三角形，它的外接球就是它扩展为正三棱柱的外接球，求出正三棱柱的底面中心连线到顶点的距离，就是球的半径，在正三棱柱中，底面边长为2，高为3，‎ 由题意得桑棱柱上下底面中点连线的中点到三棱柱顶点的距离相等，说明中心就是外接球的中心，所以，正三棱柱的外接球的球心为，外接球的半径为，表面积为，球心到底面的距离为1，‎ 底面中心到底面三角形的顶点的距离为，‎ 所以球的半径为，‎ 故外接球的表面积为.‎ ‎33.(2014湖北武汉高三2月调研测试，11) 已知某几何体的三视图如图所示，则该几何体的 表面积为        ．‎ ‎[解析] 33.  由三视图可知，该几何体是底面半径为1，高为，母线长为2的圆锥的一半. 其表面积是整个圆锥表面积的一半与轴截面的面积之和.‎ 所以，=.‎ ‎34. (2014周宁、政和一中第四次联考，15) 如图，平面四边形中，，，将其沿对角线 折成四面体，使平面平面，若四面体顶点在同一个球面上，则该球的体积为 　　             . ‎ ‎  ‎ ‎[解析] 34.   由题意，在平行四边形中，，，，将其沿对角线折成四面体，使平面平面，若四面体顶点在同一个球面上，可知，所以，是外接球的直径，所以，球的半径为，‎ 故球的体积为.‎ ‎35. (2014湖南株洲高三教学质量检测（一），11) 一几何体的三视图如下图所示，则它的体 积为            . ‎ ‎[解析] 35.   原几何体是一个正三棱柱截取一个三棱锥得到的，正三棱柱的底面三角形边长为2，底边上的高为，正三棱柱的高为2，体积为，截取的三棱锥底面积为，高为1，体积，故原几何体的体积为.‎ ‎36.(2014江苏苏北四市高三期末统考, 8) 若正三棱锥的底面边长为，侧棱长为1，则此三棱锥的体积为   ▲   ．‎ ‎[解析] 36.  正三棱锥的底面边长为，侧棱长为1，如图，过作平面，‎ 为底面正三角形的高，且，‎ 棱锥的高，‎ 三棱锥的体积为.‎ ‎37. (2014河南郑州高中毕业班第一次质量预测, 15) 已知三棱柱的侧棱垂直于底 面，各顶点都在同一球面上，若该棱柱的体积为. ，则此球的表面积等于_________. ‎ ‎[解析] 37.  三棱柱的侧棱垂直于底面，棱柱的体积为，，‎ ‎，解得，‎ 根据余弦定理得，，‎ 设外接圆的半径为，则，，‎ 外接球的半径为，球的表面积为.‎ ‎38. (2014江西七校高三上学期第一次联考, 13) 若正四棱锥的左视图如右图所示，则该正四棱锥体积为　　   . ‎ ‎[解析] 38.  依题意，这个四棱锥的底面是边长为2的正方形，侧面为等边三角形的正四棱锥，其体积 ‎.‎ 答案和解析 理数 ‎[答案] 1.  A ‎[解析] 1.  取边长为的边的中点, 并与其对棱的两个端点连接,‎ ‎[答案] 2.  B ‎[解析] 2.  该三视图对应的几何体为组合体，其中上半部为半径为3母线长为5的圆锥，下半部为底面半径为3高为5的圆柱，所以其表面积为.‎ ‎[答案] 3.  B ‎[解析] 3.  从三视图中可以看出该几何体是正四棱锥，且其斜高为底面是边长为2的正方形，故其表面积为.[学§科§网Z§X§X§K]‎ ‎[答案] 4.  B ‎[解析] 4.  三棱锥P－ABC的外接球与高为6底面边长为3的正三棱柱的外接球相同，即可把三棱锥P－ABC补成高为6底面边长为3的正三棱柱，由此可得球心O到底面ABC的距离为3，设底面ABC的外接圆圆心为O1, 连接OA, O1A、OO1, 则O1A =, OO1=3，所以OA2=O1A2+=，所以该求的体积为.‎ ‎[答案] 5.  A ‎[解析] 5.  根据三视图可知，该几何体由两部分组成，上半部为底面边长分别为3和2的长方形高为x的四棱锥，下半部为高为1底面边长分别为3和2的长方形的长方体，所以其体积为，解得x=2.‎ ‎[答案] 6.  D ‎[解析] 6.  取线段AC的中点E, 则由题意可得SE⊥AC, BE⊥AC, 则∠SEB即为二面角S-AC-B的平面角, 在△SEB中, SE=, BE=1, 根据余弦定理, 得, 在△SAB和△SCB中, 满足勾股定理, 可得SA⊥AB, SC⊥BC, 所以S、A、B、C都在同一球面上，则该球的直径是SB, 所以该球的表面积为.‎ ‎[答案] 7.  C ‎[解析] 7.  该三视图对应的几何体为由上中下三部分构成的组合体，其中上半部是长宽高分别为3、3、1的长方体；中半部为底面直径为1高为1的圆柱；下半部为长宽高分别为4、4、2的长方体，其体积为.‎ ‎[答案] 8.B ‎[解析] 8.  由三视图知，原几何体是一个三棱柱，底面是等腰直角三角形，且腰长为2，‎ 所以该三棱柱的体积.‎ ‎[答案] 9.  C ‎[解析] 9.  根据三视图可知，该几何体是一个有一条侧棱垂直于底面的四棱锥，该四棱锥的高为4，因为体积 为24，所以底面积.‎ ‎[答案] 10.  C ‎ ‎[解析] 10.  如图，当平面时，四面体体积的最大. 此时，，所以，设球半径为R，则,‎ 即，从而，故.‎ ‎[答案] 11.  D ‎[解析] 11.原几何体如图中三棱锥，由已知正视图、侧视图和俯视图均是三角形，可知该几何体有一个侧面垂直于底面，高为，底面是一个等腰直角三角形，则这个几何体的外接球的球心在高线上，且是等边三角形的中心，‎ 所以这个几何体的外接球的半径为，‎ 所以这个几何体的外接球的表面积为.‎ ‎[答案] 12.  D ‎ ‎[解析] 12.  设球半径为， 如图所示，可得，解得，所以表面积为.‎ ‎[答案] 13.D ‎ ‎[解析] 13.  由三视图知，原几何体的体积为.‎ ‎[答案] 14.D ‎[解析] 14.该几何体是一三棱柱，qi 其体积为=4.‎ ‎[答案] 15.  C ‎[解析] 15.  由三视图知，原几何体是一个三棱柱，其底边为边长为2的等边三角形，高为2，‎ 所以球心在三棱柱上下两底面的中心的连线的中点，‎ 球的半径为，球的表面积为.‎ ‎[答案] 16.  C ‎[解析] 16.  三棱锥S－ABC的外接球与高为1底面边长为1等腰直角三角形的直三棱柱的外接球相同，即可把三棱锥P－ABC补成高为1底面边长为1等腰直角三角形的直三棱柱，由此可得球心O到底面ABC的距离为，设底面ABC的外接圆圆心为O1, 连接OA, O1A、OO1, 则O1A =, OO1=，所以OA2=O1A2+=，所以该求的体积为.‎ ‎[答案] 17.  B ‎[解析] 17.  根据三视图可知，该几何体为如下图所示的四棱锥，其中PA⊥PB，底面ABCD为矩形且与侧面PAB垂直，过点P作线段AB的垂线，则该垂线即为四棱锥的高，其长度 为cm，而矩形ABCD的边长AD=5，AB=5，所以其体积为 cm3.‎ ‎[答案] 18.  B ‎[解析] 18.  该三视图对应的几何体为长、宽、高分别为6 cm、3 cm、6 cm的长方体截去一个三棱锥后所得的几何体，其体积为6×3×6－98 cm3.‎ ‎[答案] 19.  C ‎[解析] 19.  表面积等于正方体的表面积减去12个表面上的小正方形面积，加上6个棱柱的侧面积，减去6个通道的6个小正方体的表面积．则S=6×36-12+6×4×6-6×6=312．故选C．‎ ‎[答案] 20.  C[]‎ ‎[解析] 20.  根据三视图可知，该几何题是由半圆柱和直三棱柱构成的组合体，其中半圆柱的底面半径为1，高为2；直三棱柱的底面是腰长为的等腰直角三角形，故该几何体的体积为.‎ ‎[答案] 21.  ‎ ‎[解析] 21.  由几何体的三视图可知，该几何体是一个沿旋转轴作截面，截取的半个圆锥，底面半径是1，高是2，所以母线长为，所以其表面积为底面半圆面积和圆锥的侧面积的一半以及截面三角形的面积的和，即，故选.‎ ‎[答案] 22.  D ‎[解析] 22.  根据几何概型，‎ ‎=== ，‎ 其中“＝” 当且仅当时成立. 故选D.‎ ‎[答案] 23.  B ‎[解析] 23.   由三视图知，原几何体是由一个半圆柱与一个半圆锥构成，其体积为.‎ ‎[答案] 24.  C ‎[解析] 24.由已知，元几何体为四棱柱，其底面边长为，侧视图的高为，‎ 底面积为，又因为棱柱的高为3，侧面积为，‎ 故原几何体的表面积为.‎ ‎[答案] 25.C ‎[解析] 25.由三视图可知，该几何体是由三个棱长为1的正方体加半个正方体构成，所以体积为 ‎[答案] 26.  C ‎[解析] 26.画出直观图可知，原几何体的体积.‎ ‎[答案] 27.  C ‎[解析] 27.  原几何体是由一个圆柱与一个圆锥构成，其体积为.‎ ‎[答案] 28.  ‎ ‎[解析] 28.  该三视图对应的几何体为组合体, 其中上半部为底面边长为2, 斜高为的正四棱锥, 下半部分是边长为2的正方体, 所以其表面积为.‎ ‎[答案] 29.‎ ‎[解析] 29.  由三视图知，原几何体是一个棱长为2的正方体削去一个三棱锥后剩下的一个七面体 ‎，截面三角形为边长为的等边三角形，截面的面积为，‎ 所以几何体的表面积为.‎ ‎[答案] 30.‎ ‎[解析] 30.因为底面正方形的四个顶点在球面上，所以四个顶点在一个小圆面上，且与是小圆直径. 所以，，又，从而由+得：，故.‎ ‎[答案] 31.  12‎ ‎[解析] 31.  根据三视图可知，该几何体是底面为以2和3为直角边的直角三角形高为4的三棱柱，其体积为.‎ ‎[答案] 32.‎ ‎[解析] 32.  根据题意知，三棱锥的三条侧棱，，底面是正三角形，它的外接球就是它扩展为正三棱柱的外接球，求出正三棱柱的底面中心连线到顶点的距离，就是球的半径，在正三棱柱中，底面边长为2，高为3，‎ 由题意得桑棱柱上下底面中点连线的中点到三棱柱顶点的距离相等，说明中心就是外接球的中心，所以，正三棱柱的外接球的球心为，外接球的半径为，表面积为，球心到底面的距离为1，‎ 底面中心到底面三角形的顶点的距离为，‎ 所以球的半径为，‎ 故外接球的表面积为.‎ ‎[答案] 33.  ＋‎ ‎[解析] 33.  由三视图可知，该几何体是底面半径为1，高为，母线长为2的圆锥的一半. 其表面积是整个圆锥表面积的一半与轴截面的面积之和.‎ 所以，=.‎ ‎[答案] 34.  ‎ ‎[解析] 34.   由题意，在平行四边形中，，，，将其沿 对角线折成四面体，使平面平面，若四面体顶点在同一个球面上，可知，所以，是外接球的直径，所以，球的半径为，‎ 故球的体积为.‎ ‎[答案] 35.  ‎ ‎[解析] 35.   原几何体是一个正三棱柱截取一个三棱锥得到的，正三棱柱的底面三角形边长为2，底边上的高为，正三棱柱的高为2，体积为，截取的三棱锥底面积为，高为1，体积，故原几何体的体积为.‎ ‎[答案] 36.  ‎ ‎[解析] 36.  正三棱锥的底面边长为，侧棱长为1，如图，过作平面，‎ 为底面正三角形的高，且，‎ 棱锥的高，‎ 三棱锥的体积为.‎ ‎[答案] 37.  ‎ ‎[解析] 37.  三棱柱的侧棱垂直于底面，棱柱的体积为，，‎ ‎，解得，‎ 根据余弦定理得，，‎ 设外接圆的半径为，则，，‎ 外接球的半径为，球的表面积为.‎ ‎[答案] 38.  ‎ ‎[解析] 38.  依题意，这个四棱锥的底面是边长为2的正方形，侧面为等边三角形的正四棱锥，其体积 ‎.‎