高考直线方程题型归纳 8页

高考直线方程题型归纳 知识点梳理 ‎1．点斜式方程 ‎ 设直线l过点P0(x0，y0)，且斜率为k，则直线的方程为y－y0=k(x－x0)，‎ 由于此方程是由直线上一点P0(x0，y0)和斜率k所确定的直线方程，我们把这个方程叫做直线的点斜式方程.‎ 注意：利用点斜式求直线方程时，需要先判断斜率存在与否.‎ ‎（1）当直线l的倾斜角α=90°时，斜率k不存在，不能用点斜式方程表示，但这时直线l恰与y轴平行或重合，这时直线l上每个点的横坐标都等于x0，所以此时的方程为x=x0.‎ ‎（2）当直线l的倾斜角α=0°时，k=0，此时直线l的方程为y=y0，即y－y0=0.‎ ‎（3）当直线l的倾斜角不为0°或90°时，可以直接代入方程求解.‎ ‎2．斜截式方程：如果一条直线通过点(0，b)且斜率为k，则直线的点斜式方程为y=kx+ b 其中k为斜率，b叫做直线y=kx+b在y轴上的截距，简称直线的截距.‎ ‎ 注意：利用斜截式求直线方程时，需要先判断斜率存在与否.‎ ‎（1）并非所有直线在y轴上都有截距，当直线的斜率不存在时，如直线x=2在y轴上就没有截距，即只有不与y轴平行的直线在y轴上有截距，从而得斜截式方程不能表示与x轴垂直的直线的方程.‎ ‎（2）直线的斜截式方程y=kx+b是y关于x的函数，当k=0时，该函数为常量函数.x=b；当k≠0时，该函数为一次函数，且当k>0时，函数单调递增，当k<0时，函数单调递减.‎ ‎（3）直线的斜截式方程是直线的点斜式方程的特例。要注意它们之间的区别和联系及其相互转化.‎ ‎3．直线的两点式方程 若直线l经过两点A(x1，y1)，B(x2，y2)，(x1≠x2)，则直线l的方程为，这种形式的方程叫做直线的两点式方程.‎ ‎ 注意 ‎ （1）当直线没有斜率(x1=x2)或斜率为零(y1=y2)时，不能用两点式表示它的方程；‎ ‎ （2）可以把两点式的方程化为整式(x2－x1)(y－y1)= (y2－y1)(x－x1)，就可以用它来求过平面上任意两点的直线方程； 如过两点A(1，2)，B(1，3)的直线方程可以求得x=1，过两点A(1，3)，B(－2，3)的直线方程可以求得y=3.‎ ‎ （3）需要特别注意整式(x2－x1)(y－y1)= (y2－y1)(x－x1)与两点式方程的区别，前者对于任意的两点都适用，而后者则有条件的限制，两者并不相同，前者是后者的拓展。‎ ‎4．直线的截距式方程 若直线l在x轴上的截距是a，在y轴上的截距是b，且a≠0，b≠0，则直线l的方程为 ‎，这种形式的方程叫做直线的截距式方程。‎ ‎ 注意：‎ ‎ （1）方程的条件限制为a≠0，b≠0，即两个截距均不能为零，因此截距式方程不能表示过原点的直线以及与坐标轴平行的直线；‎ ‎ （2）用截距式方程最便于作图，要注意截距是坐标而不是长度；‎ ‎ （3）要注意“截距相等”与“截距绝对值相等”是两个不同的概念，截距式中的截距可正、可负，但不可为零。‎ ‎ 截距式方程的应用 ‎（1）与坐标轴围成的三角形的周长为：|a|+|b|+；‎ ‎（2）直线与坐标轴围成的三角形面积为：S= ；‎ ‎（3）直线在两坐标轴上的截距相等，则k=－1或直线过原点，常设此方程为x+y=a或y=kx.‎ ‎5．直线方程的一般形式 ‎ 方程Ax+By+C=0（A、B不全为零）叫做直线的一般式方程.‎ ‎ 注意 ‎（1）．两个独立的条件可求直线方程：‎ 求直线方程，表面上需求A、B、C三个系数，由于A、B不同时为零，‎ 若A≠0，则方程化为，只需确定的值；‎ 若B≠0，同理只需确定两个数值即可；‎ 因此，只要给出两个条件，就可以求出直线方程；‎ ‎（2）．直线方程的其他形式都可以化成一般式，解题时，如果没有特殊说明应把最后结果化为一般式，一般式也可以化为其他形式。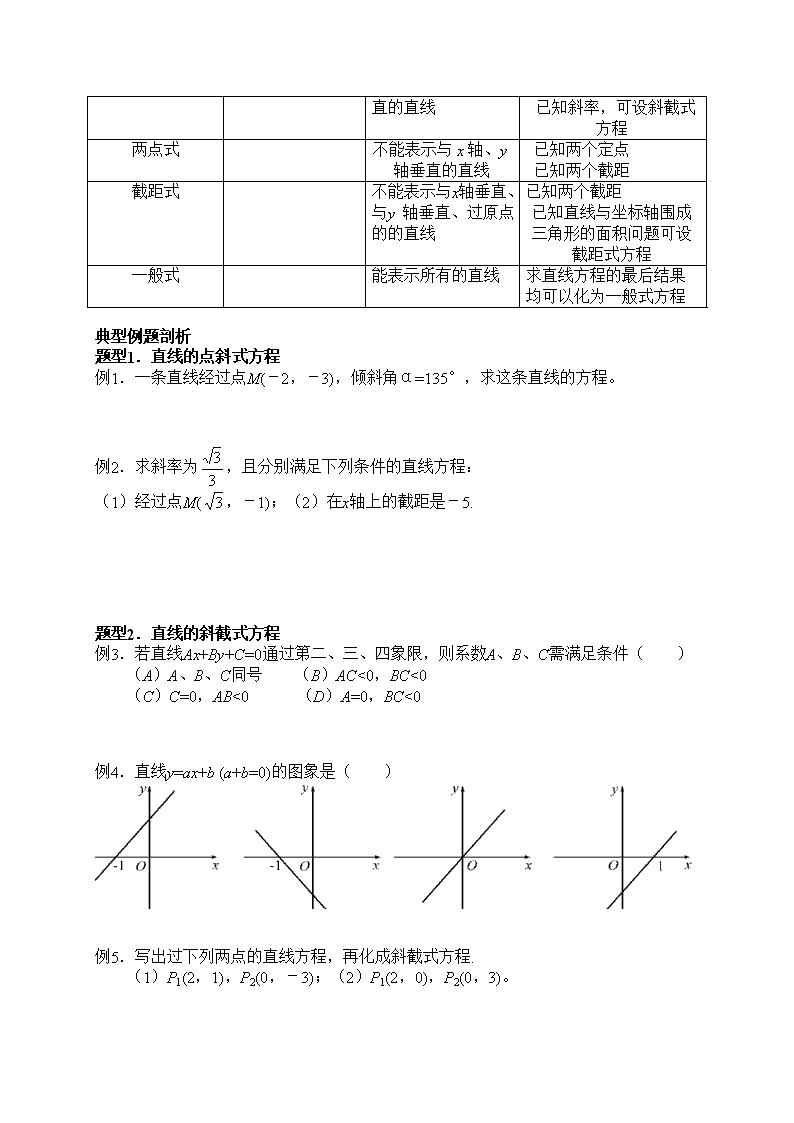‎ ‎（3）．在一般式Ax+By+C=0（A、B不全为零）中，‎ 若A=0，则y=，它表示一条与y轴垂直的直线；‎ 若B=0，则，它表示一条与x轴垂直的直线.‎ ‎6.直线方程的选择 ‎（1）待定系数法是求直线方程的最基本、最常用的方法，但要注意选择形式，一般地已知一点，可以待定斜率k，但要注意讨论斜率k不存在的情形，如果已知斜率可以选择斜截式待定截距等；‎ ‎（2）直线方程的几种特殊形式都有其使用的局限性，解题过程中要能够根据不同的题设条件，灵活选用恰当的直线形式求直线方程。请参看下表：‎ 直线形式 直线方程 局限性 选择条件 点斜式 不能表示与x轴垂直的直线 已知一个定点和斜率k ‎ 已知一点，可设点斜式方程 斜截式 不能表示与x 已知在y轴上的截距 轴垂直的直线 ‎ 已知斜率，可设斜截式方程 两点式 不能表示与x轴、y轴垂直的直线 已知两个定点 已知两个截距 截距式 不能表示与x轴垂直、与y 轴垂直、过原点的的直线 已知两个截距 已知直线与坐标轴围成三角形的面积问题可设截距式方程 一般式 能表示所有的直线 求直线方程的最后结果均可以化为一般式方程 典型例题剖析 题型1．直线的点斜式方程 例1．一条直线经过点M(－2，－3)，倾斜角α=135°，求这条直线的方程。‎ 例2．求斜率为，且分别满足下列条件的直线方程：‎ ‎（1）经过点M(，－1)；（2）在x轴上的截距是－5.‎ 题型2．直线的斜截式方程 例3．若直线Ax+By+C=0通过第二、三、四象限，则系数A、B、C需满足条件（ ）‎ ‎（A）A、B、C同号 （B）AC<0，BC<0 ‎ ‎（C）C=0，AB<0 （D）A=0，BC<0‎ 例4．直线y=ax+b (a+b=0)的图象是（ ）‎ 例5．写出过下列两点的直线方程，再化成斜截式方程.‎ ‎ （1）P1(2，1)，P2(0，－3)；（2）P1(2，0)，P2(0，3)。‎ 例6． 三角形的顶点是A(－5，0)、B(3，－3)、C(0，2)，求这个三角形三边所在的直线方程.‎ 题型4．直线的截距式方程 例7．已知直线的斜率为，且和坐标轴围成面积为3的三角形，求该直线的方程。‎ 例8．过点A(1，4)且纵截距与横截距的绝对值相等的直线共有的条数为（ ）‎ ‎ （A）1 （B）2 （C）3 （D）4‎ 题型5．直线的一般式方程 例9．已知直线经过点A(6，－4)，斜率为－，求直线的点斜式和一般式方程.‎ 例10．把直线l的方程x－2y+6=0化成斜截式，求出直线l的斜率和它在x轴与y轴上的截距，并画图.‎ 题型6.定点问题 例11、已知直线所过定点的横、纵坐标分别是等差数列{}的第一项与第二项，若，数列的前n项和为Tn，则T10=（    ）‎ ‎   A.      B.     C.      D.‎ 题型7.对称问题 例12、已知直线l1：y＝2x＋3，直线l2与l1关于直线y＝－x对称，则直线l2的斜率为(　　)‎ A.      B．－  C．2        D．－2‎ 例13、直线关于直线对称的直线方程是    （    ）‎ ‎    A．       B． ‎ ‎    C．       D． ‎ 例14、直线2x－y－4=0上有一点P，它与两定点A(4，－1)，B(3，4)的距离之差最大，则P点坐标是_________  ‎ 例15.(1)求点A(3,2)关于点B(－3,4)的对称点C的坐标；‎ ‎ (2)求直线3x－y－4＝0关于点P(2，－1)对称的直线l的方程；‎ ‎ (3)求点A(2,2)关于直线2x－4y＋9＝0的对称点的坐标．‎ 题型8.最值问题 例16、若点(m，n)在直线4x＋3y－10＝0上，则m2＋n2的最小值是(　　)‎ A．2       B．2  C．4       D．2‎ 例17、直线与直线互相垂直，则的最小值为（   ）‎ A．1       B．2        C．4   D．5 ‎ 例18.过点P(1，2)作直线l，交x，y轴的正半轴于A、B两点，求使△OAB 面积取得最小值时直线l的方程.‎ 题型9．创新问题 例19．已知两直线a1x+b1y+1=0和a2x+b2y+1=0的交点为P(2，3)，求过两点Q1(a1，b1)，Q2(a2，b2)的直线方程.‎ 例20、已知点A(－1,0)，B(1,0)，C(0,1)，直线y＝ax＋b(a>0)将△ABC分割为面积相等的两部分，则b的取值范围是(　　)‎ A．(0,1)     B. C.       D. ‎ 例21、在平面直角坐标系中，定义d（P，Q）=|x1﹣x2|+|y1﹣y2|为两点P（x1，y1），Q（x2，y2）之间的“折线距离”，在这个定义下，给出下列命题：‎ ‎①到原点的“折线距离”等于1的点的集合是一个圆；‎ ‎②到原点的“折线距离”小于等于2的点构成的区域面积为8；‎ ‎③到M（0，﹣2），N（0，2）两点的“折线距离”相等的点的轨迹方程是y=0；‎ ‎④直线y=x+1上的点到N（0，2）的“折线距离”的最小值为1．‎ 其中真命题有（　　）‎ ‎　‎ A．‎ ‎1个 B．‎ ‎2个 C．‎ ‎3个 D．‎ ‎4个 例22、已知两定点M（-2，0），N（2，0），若直线上存在点P，使得，则该称直线为“A型直线”.给出下列直线：‎ ‎①，    ②，    ③，    ④，‎ 其中是“A型直线”的序号是         .‎ 例23、已知直线l：(A，B不全为0)，两点，，若，且，则（   ）‎ A．直线l与直线P1P2不相交         B．直线l与线段P2 P1的延长线相交 C．直线l与线段P1 P2的延长线相交      D．直线l与线段P1P2相交 ‎ 例24. 已知实数x，y满足y＝x2－2x＋2(－1≤x≤1)．试求的最大值与最小值．‎ 强化训练 ‎1．下列说法中不正确的是（ ）‎ ‎（A）点斜式y－y0=k(x－x0)适用于不垂直于x轴的任何直线 ‎ ‎（B）斜截式y=kx+b适用于不垂直x轴的任何直线 ‎ ‎（C）两点式适用于不垂直于坐标轴的任何直线 ‎ ‎（D）截距式适用于不过原点的任何直线 ‎2．直线3x－2y=4的截距式方程为（ ）‎ ‎ （A） （B） （C） （D）‎ ‎3．过点(3，－4)且平行于x轴的直线方程是 ；过点(5，－2)且平行于y轴的直线方程是 。‎ ‎4．过点P(1，3)的直线分别与两坐标轴交于A、B两点，若P为AB的中点，求直线的方程. ‎ ‎5．已知△ABC中，A(1，－4)，B(6，6)，C(－2，0)，求：‎ ‎（1）△ABC的平行于BC边的中位线的一般式方程和截距式方程；‎ ‎（2）BC边的中线的一般式方程，并化为截距式方程.‎ ‎ ‎ ‎6．如果AC<0，BC<0，那么直线Ax+By+C=0不通过（ ）‎ ‎ （A）第一象限 （B）第二象限 （C）第三象限 （D）第四象限 ‎7．直线l过点P(1，3)，且与x，y轴正半轴所围成的三角形的面积等于6，则l的方程是（ ）‎ ‎ （A）3x+y－6=0 （B）x+3y－10=0 （C）3x－y=0 （D）x－3y+8=0‎ ‎8．若直线(2m2+m－3)x+(m2－m)y=4m－1在x轴上的截距为1，则实数m是（ ）‎ ‎ （A）1 （B）2 （C）－ （D）2或－‎ ‎9．已知直线l：Ax+By+C=0(A2+B2≠0)，点P(x0，y0)在l上，则l的方程可化为（ ）‎ ‎（A）A(x+x0)+B(y+y0)+C=0 （B）A(x+x0)+B(y+y0)=0 ‎ ‎（C）A(x－x0)+B(y－y0)+C=0 （D）A(x－x0)+B(y－y0)=0‎ ‎10．经过点(－3，－2)，在两坐标轴上截距相等的直线方程为 ‎ ‎ ‎ ‎11．若点(a，12)在过点(1，3)及点(5，7)的直线上，则a= .‎ ‎12．、在平面直角坐标系中，是坐标原点，设函数的图象为直线，且与轴、轴分别交于、两点，给出下列四个命题：‎ ‎①     存在正实数，使△的面积为的直线仅有一条；‎ ‎②     存在正实数，使△的面积为的直线仅有两条；‎ ‎③     存在正实数，使△的面积为的直线仅有三条；‎ ‎④     存在正实数，使△的面积为的直线仅有四条.‎ 其中所有真命题的序号是          .‎ 13、 在平面直角坐标系xOy中，设点、，定义：． 已知点，点M为直线上的动点，则使取最小值时点M的坐标是    ． ‎ ‎14（1）已知直线l：(2m2+m－3)x+(m2－m)y－4m+1=0，求m的取值范围#‎ ‎ （2）如果ab>0，bc<0，那么直线ax－by－c必经过第几象限？‎