新教材高中物理第3章圆周运动拓展课水平与竖直面内的圆周运动学案鲁科版必修第二册 12页

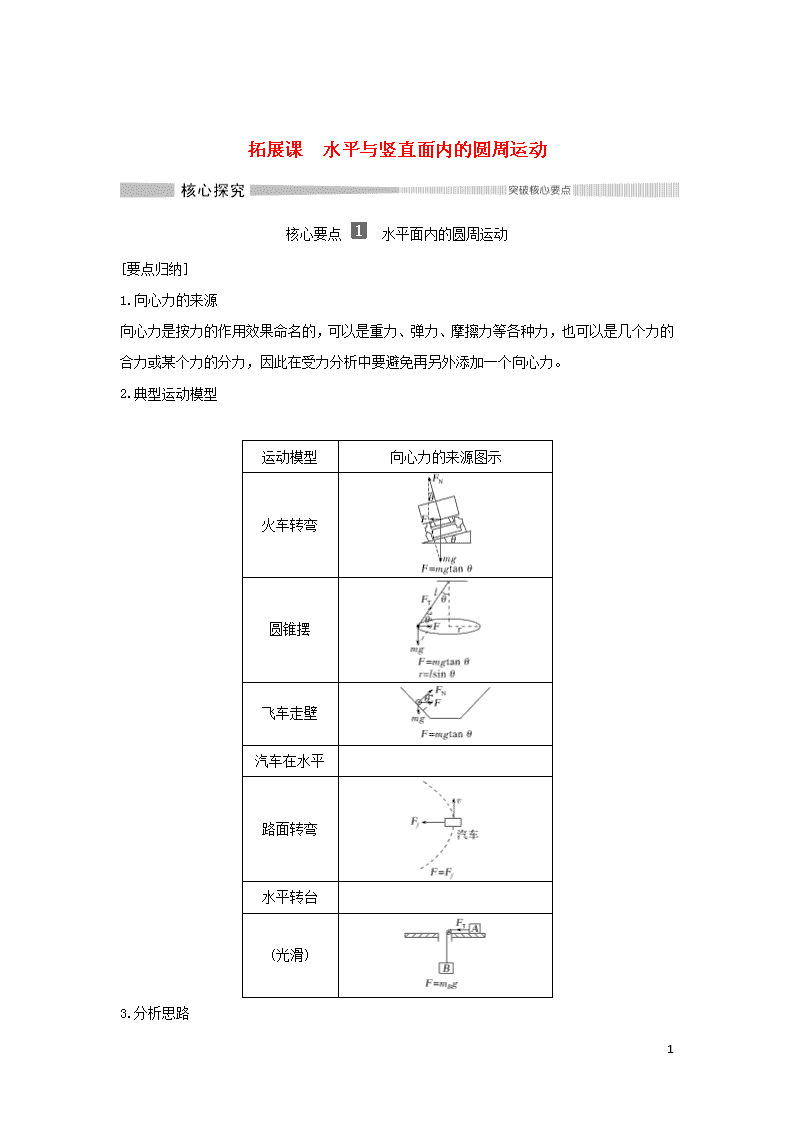
拓展课　水平与竖直面内的圆周运动 核心要点 　水平面内的圆周运动 ‎[要点归纳]‎ ‎1.向心力的来源 向心力是按力的作用效果命名的，可以是重力、弹力、摩擦力等各种力，也可以是几个力的合力或某个力的分力，因此在受力分析中要避免再另外添加一个向心力。‎ ‎2.典型运动模型 运动模型 向心力的来源图示 火车转弯 圆锥摆 飞车走壁 汽车在水平 路面转弯 水平转台 ‎(光滑)‎ ‎3.分析思路 12‎ ‎(1)选择研究对象，找出匀速圆周运动的圆心和半径。‎ ‎(2)分析物体受力情况，其合外力提供向心力。‎ ‎(3)由F＝m或F＝mrω2或F＝mr列方程求解。‎ ‎[经典示例]‎ ‎[例1] (多选)如图，两个质量均为m的小木块a和b(可视为质点)放在水平圆盘上，a与转轴OO′的距离为l，b与转轴的距离为2l，木块与圆盘的最大静摩擦力为木块所受重力的k倍，重力加速度大小为g。若圆盘从静止开始绕转轴缓慢地加速转动，用ω表示圆盘转动的角速度，下列说法正确的是(　　)‎ A.b一定比a先开始滑动 B.a、b所受的摩擦力始终相等 C.ω＝ 是b开始滑动的临界角速度 D.当ω＝ 时，a所受摩擦力的大小为kmg 解析　因圆盘从静止开始绕转轴缓慢加速转动，在某一时刻可认为，木块随圆盘转动时，其受到的静摩擦力的方向指向转轴，两木块转动过程中角速度相等，则根据牛顿第二定律可得f＝mω2R，由于小木块b的轨道半径大于小木块a的轨道半径，故小木块b做圆周运动需要的向心力较大，B项错误；因为两小木块的最大静摩擦力相等，故b一定比a先开始滑动，A项正确；当b开始滑动时，由牛顿第二定律可得kmg＝mω·2l，可得ωb＝ ，C项正确；当a开始滑动时，由牛顿第二定律可得kmg＝mωl，可得ωa＝，而转盘的角速度ω＝<，小木块a未发生滑动，其所需的向心力由静摩擦力来提供，由牛顿第二定律可得f＝mω2l＝kmg，D项错误。‎ 答案　AC ‎[针对训练1] (多选)在修筑铁路时，弯道处的外轨会略高于内轨。如图所示，当火车以规定的行驶速度转弯时，内、外轨均不会受到轮缘的挤压，设此时的速度大小为v，重力加速度大小为g，两轨所在面的倾角为θ，则(　　)‎ 12‎ A.该弯道的半径r＝ B.当火车质量改变时，规定的行驶速度大小不变 C.当火车速率大于v时，内轨将受到轮缘的挤压 D.当火车速率大于v时，外轨将受到轮缘的挤压 解析　火车转弯时不侧向挤压车轮轮缘，靠重力和支持力的合力提供向心力，根据牛顿第二定律得mgtan θ＝m，解得r＝，故A正确；根据牛顿第二定律得mgtan θ＝m，解得v＝，可知火车规定的行驶速度与质量无关，故B正确；当火车速率大于v时，重力和支持力的合力不足以提供向心力，此时外轨对火车有侧压力，轮缘挤压外轨，故C错误，D正确。‎ 答案　ABD 核心要点 　竖直面内的圆周运动 ‎[要点归纳]‎ 两类模型比较 球—绳模型 球—杆模型 实例 如球与绳连接、沿内轨道运动的球等 如球与轻杆连接、球在内壁光滑的圆管内运动等 图示 最高点无支撑 最高点有支撑 最高点 受力特征 重力、弹力，弹力方向向下或等于零 重力、弹力，弹力方向向下、等于零或向上 12‎ 受力示意图 力学特征 mg＋FN＝m mg±FN＝m 临界特征 FN＝0，vmin＝ 竖直向上的FN＝mg，v＝0‎ 过最高点条件 v≥ v≥0‎ 速度和弹力关系讨论分析 ‎①恰好过最高点时，v＝，mg＝m，FN＝0，绳、轨道对球无弹力 ‎②能过最高点时，v≥，FN＋mg＝m，绳、轨道对球产生弹力FN ‎③不能过最高点时，v<，在到达最高点前小球已经脱离了圆轨道做斜抛运动 ‎①当v＝0时，FN＝mg，FN为支持力，沿半径背离圆心 ‎②当0时，FN＋mg＝m，FN指向圆心并随v的增大而增大 ‎[经典示例]‎ ‎[例2] (多选)如图所示，竖直环A半径为r，固定在木板B上，木板B放在水平地面上，B的左、右两侧各有一挡板固定在地上，B不能左、右运动，在环的最低点静放有一小球C，A、B、C的质量均为m。现给小球一水平向右的瞬时速度v，小球会在环内侧做圆周运动。为保证小球能通过环的最高点，且不会使环在竖直方向上跳起(不计小球与环的摩擦阻力，重力加速度为g)，则瞬时速度v必须满足(　　)‎ A.最小值为 B.最大值为 C.最小值为 D.最大值为 12‎ 解析　要保证小球能通过环的最高点，在最高点最小速度满足mg＝m，由最低点到最高点由机械能守恒得mv＝mg·2r＋mv，可得小球在最低点瞬时速度的最小值为，A错误，C正确；为了使环不会在竖直方向上跳起，则在最高点球有最大速度时，对环的压力为2mg，满足3mg＝m，从最低点到最高点由机械能守恒得mv＝mg·2r＋mv，可得小球在最低点瞬时速度的最大值为，B错误，D正确。‎ 答案　CD ‎[针对训练2] 如图所示，长为3L的轻杆可绕水平转轴O转动，在杆两端分别固定质量均为m的球A、B(可视为质点)，球A距轴O的距离为L。现给系统一定动能，使杆和球在竖直平面内转动。当球B运动到最高点时，水平转轴O对杆的作用力恰好为零，忽略空气阻力。已知重力加速度为g，则球B在最高点时，下列说法正确的是(　　)‎ A.球B的速度为0 B.杆对球B的弹力为0‎ C.球B的速度为 D.球A的速度等于 解析　对B球：T＋mg＝m，对A球：T ′－mg＝m，同时vB＝2vA，要使轴O对杆作用力为0，即满足T＝T ′，解得vA＝，vB＝2，故只有D项正确。‎ 答案　D ‎1.(水平面内的圆周运动)(多选)公路急转弯处通常是交通事故多发地带。如图所示，某公路急转弯处是一圆弧，当汽车行驶的速率为vc时，汽车恰好没有向公路内、外两侧滑动的趋势，则在该弯道处(　　)‎ A.路面外侧高、内侧低 B.车速只要低于vc，车辆便会向内侧滑动 12‎ C.车速虽然高于vc，但只要不超出某一最高限度，车辆便不会向外侧滑动 D.当路面结冰时，与未结冰时相比，vc的值变小 解析　当汽车行驶的速率为vc时，路面对汽车没有摩擦力，路面对汽车的支持力与汽车重力的合力提供向心力，此时要求路面外侧高、内侧低，选项A正确；当速度稍大于vc时，汽车有向外侧滑动的趋势，因而受到向内侧的摩擦力，当摩擦力小于最大静摩擦力时，车辆不会向外侧滑动，选项C正确；同样，速度稍小于vc时，车辆不会向内侧滑动，选项B错误；vc的大小只与路面的倾斜程度和转弯半径有关，与路面的粗糙程度无关，D错误。‎ 答案　AC ‎2.(水平面内的圆周运动)如图所示，将一质量为m的摆球用长为L的细绳吊起，上端固定，使摆球在水平面内做匀速圆周运动，细绳就会沿圆锥面旋转，这样就构成了一个圆锥摆，则关于摆球的受力情况，(不计空气阻力)下列说法中正确的是(　　)‎ A.摆球受重力、拉力和向心力的作用 B.摆球受拉力和向心力的作用 C.摆球受重力和拉力的作用 D.摆球受重力和向心力的作用 解析　我们在进行受力分析时，“物体受到哪几个力的作用”中的力是指按照性质命名的力，显然，物体只受重力G和拉力FT的作用，而向心力F是重力和拉力的合力，如图所示。也可以认为向心力就是FT沿水平方向的分力FT2，显然，FT沿竖直方向的分力FT1与重力G平衡。所以，本题正确选项为C。‎ 答案　C ‎3.(竖直面内的圆周运动)如图所示，轻质且不可伸长的细绳一端系一质量为m的小球，另一端固定在天花板上的O点。则小球在竖直平面内摆动的过程中，以下说法正确的是(　　)‎ A.小球在摆动过程中受到的外力的合力即为向心力 12‎ B.在最高点A、B，因小球的速度为零，所以小球受到的合力为零 C.小球在最低点C所受的合力，即为向心力 D.小球在摆动过程中绳子的拉力使其速率发生变化 解析　小球摆动过程中，合力沿绳子方向的分力提供向心力，不是靠外力的合力提供向心力，故A错误；在最高点A和B，小球的速度为零，向心力为零，但是小球所受的合力不为零，故B错误；小球在最低点受重力和拉力，两个力的合力竖直向上，合力等于向心力，故C正确；小球在摆动的过程中，由于绳子的拉力与速度方向垂直，则拉力不做功，拉力不会使小球速率发生变化，故D错误。‎ 答案　C ‎4.(竖直面内的圆周运动)如图所示，某同学用硬塑料管和一个质量为m的铁质螺丝帽研究匀速圆周运动，将螺丝帽套在塑料管上，手握塑料管使其保持竖直并在水平方向做半径为r的匀速圆周运动，则只要运动角速度合适，螺丝帽恰好不下滑，假设螺丝帽与塑料管间的动摩擦因数为μ，认为最大静摩擦力近似等于滑动摩擦力。则在该同学转动塑料管使螺丝帽恰好不下滑时，重力加速度大小为g，下述分析正确的是(　　)‎ A.螺丝帽受的重力与最大静摩擦力平衡 B.螺丝帽受到杆的弹力方向水平向外，背离圆心 C.此时手转动塑料管的角速度ω＝ D.若杆的转动加快，螺丝帽有可能相对杆发生运动 解析　由于螺丝帽做圆周运动过程中恰好不下滑，则竖直方向上重力与最大静摩擦力平衡，杆对螺丝帽的弹力提供其做匀速圆周运动的向心力，选项A正确，选项B错误；由μFN＝mg 12‎ 和FN＝mrω2得ω＝，选项C错误；无论杆的转动速度增大多少，竖直方向受力始终平衡，故选项D错误。‎ 答案　A ‎1.如图所示，小物体P放在水平圆盘上随圆盘一起转动，下列关于小物体所受摩擦力f的叙述正确的是(　　)‎ A.f的方向总是指向圆心 B.圆盘匀速转动时f＝0‎ C.在物体与轴O的距离一定的条件下，f跟圆盘转动的角速度成正比 D.在转速一定的条件下，f跟物体到轴O的距离成正比 解析　物体随圆盘转动过程中，如果圆盘匀速转动，则摩擦力指向圆心，如果变速转动，则摩擦力的一个分力充当向心力，另一个分力产生切向加速度，摩擦力不指向圆心，A、B错误；根据公式F＝f＝mω2r可得在物体与轴O的距离一定的条件下，f跟圆盘转动的角速度的平方成正比，C错误；因为ω＝2πn，所以f＝m(2πn)2r，即转速一定的条件下，f跟物体到轴O的距离成正比，D正确。‎ 答案　D ‎2.如图所示，质量为m的物体，沿着半径为R的半球形金属壳内壁滑下，半球形金属壳竖直固定放置，开口向上，滑到最低点时速度大小为v，若物体与球壳之间的动摩擦因数为μ，重力加速度大小为g，则物体在最低点时，下列说法正确的是(　　)‎ A.受到的向心力为mg＋m B.受到的摩擦力为μm C.受到的摩擦力为μ(mg＋m)‎ D.受到的合力方向斜向左上方 12‎ 解析　物体做圆周运动经过最低点时，则有N－mg＝m，解得N＝mg＋m，故物体受到的滑动摩擦力f＝μN＝μ(mg＋m)，A、B错误，C正确；物体受到竖直向下的重力、水平向左的摩擦力和竖直向上的支持力(支持力大于重力)，故物体所受的合力斜向左上方，D正确。‎ 答案　CD ‎3.质量不计的轻质弹性杆P插入桌面上的小孔中，杆的另一端套有一个质量为m的小球，今使小球在水平面内做半径为R的匀速圆周运动，且角速度为ω，重力加速度大小为g，不计空气阻力。如图所示，则杆的上端受到球对其作用力的大小为(　　)‎ A.mω2R B.m C.m D.不能确定 解析　对小球进行受力分析，小球受两个力：一个是重力mg，另一个是杆对小球的作用力F，两个力的合力产生向心力。由平行四边形定则可得F＝m，再根据牛顿第三定律，可知杆受到球对其作用力的大小为F＝m。故选项C正确。‎ 答案　C ‎4.(多选)铁路在弯道处的内外轨道高低是不同的，已知内外轨道对水平面倾角为θ，弯道处的圆弧半径为R，若质量为m的火车以速度v通过某弯道时，内、外轨道均不受侧压力作用，重力加速度大小为g。下面分析正确的是(　　) ‎ A.轨道半径R＝ B.v＝ C.若火车速度小于v时，外轨将受到侧压力作用，其方向平行轨道平面向内 D.若火车速度大于v时，外轨将受到侧压力作用，其方向平行轨道平面向外 解析　火车转弯时受力如图所示，火车转弯的向心力由重力和支持力的合力提供，则mgtan ‎ 12‎ θ＝m，故转弯半径R＝；转弯时的速度v＝；若火车速度小于v时，需要的向心力小于mgtan θ，此时内轨对车轮产生一个向外的作用力，即车轮挤压内轨；若火车速度大于v时，需要的向心力大于mgtan θ，外轨对车轮产生一个向里的作用力，即车轮挤压外轨。‎ 答案　BD ‎5.轻杆一端固定有质量为m＝1 kg的小球，另一端安装在水平转轴上，转轴到小球的距离为50 cm，转轴固定在三角形的带电动机(电动机没画出来)的支架上，在电动机作用下，轻杆在竖直面内做匀速圆周运动，如图所示。若转轴达到某一恒定转速n时，在最高点，杆受到小球的压力为2 N，重力加速度g取10 m/s2。则(　　)‎ A.小球运动到最高点时，小球需要的向心力为12 N B.小球运动到最高点时，线速度v＝1 m/s C.小球运动到图示水平位置时，地面对支架的摩擦力为8 N D.把杆换成轻绳，同样转速的情况下，小球仍能通过图示的最高点 解析　小球运动到最高点时，杆受到小球的压力为2 N，由牛顿第三定律可知杆对小球的支持力FN＝2 N，在最高点，小球需要的向心力由重力和杆的支持力的合力提供，为F＝mg－FN＝8 N，故A错误；在最高点，由F＝m得，v＝＝ m/s＝2 m/s，故B错误；小球运动到图示水平位置时，设杆对小球的拉力为FT，则有FT＝m＝F＝8 N，则小球对杆的拉力FT′＝FT＝8 N，据题意知支架处于静止状态，由平衡条件可知地面对支架的摩擦力Ff＝FT′＝8 N，故C正确；把杆换成轻绳，设小球通过最高点的最小速度为v0，由mg＝m得，v0＝＝ m/s＝ m/s＞v，所以在同样转速的情况下，小球不能通过图示的最高点，故D错误。‎ 12‎ 答案　C ‎6.(多选)甲、乙两名溜冰运动员，m甲＝80 kg，m乙＝40 kg，面对面拉着弹簧测力计做圆周运动的溜冰表演，如图所示，两人相距0.9 m，弹簧测力计的示数为9.2 N，下列判断正确的是(　　)‎ A.两人的线速度相同，约为40 m/s B.两人的角速度相同，为 rad/s C.两人的运动半径相同，都是0.45 m D.两人的运动半径不同，甲为0.3 m，乙为0.6 m 解析　甲、乙两人绕共同的圆心做匀速圆周运动，他们间的拉力互为向心力，他们的角速度相同，半径之和为两人的距离。设甲、乙两人所需向心力为F向，角速度为ω，半径分别为r甲、r乙，则F向＝m甲ω2r甲＝m乙ω2r乙＝9.2 N，r甲＋r乙＝0.9 m，代入数据解得r甲＝0.3 m，r乙＝0.6 m，ω＝ rad/s，v＝ m/s，故选项B、D正确。‎ 答案　BD ‎7.有一种叫“飞椅”的游乐项目，示意图如图所示，长为L的钢绳一端系着座椅，另一端固定在半径为r的水平转盘边缘。转盘可绕穿过其中心的竖直轴转动，当转盘以角速度ω匀速转动时，钢绳与转轴在同一竖直平面内，与竖直方向的夹角为θ。不计钢绳的重力，求转盘转动的角速度ω与夹角θ的关系。‎ 解析　设转盘转动的角速度为ω，钢绳与竖直方向的夹角为θ，‎ 座椅到中心的距离为R＝r＋Lsin θ，‎ 对座椅分析有F＝mgtan θ＝mRω2，‎ 联立两式得ω＝。‎ 12‎ 答案　ω＝ ‎8.如图所示，一条不可伸长的轻绳上端悬挂于O点，下端系一质量m＝1.0 kg的小球。现将小球拉到A点(保持轻绳绷直)由静止释放，当它经过B点时轻绳恰好被拉断，小球平抛后落在水平地面上的C点，地面上的D点与OB在同一竖直线上。已知轻绳长L＝1.0 m，B点离地高度 H＝1.0 m，A、B两点的高度差h＝0.5 m，重力加速度g取10 m/s2，不计空气阻力，求：‎ ‎(1)地面上D、C两点间的距离s；‎ ‎(2)轻绳所受的最大拉力大小。‎ 解析　(1)小球从A点到B点机械能守恒，则 mgh＝mv 小球从B点到C点做平抛运动，则水平方向s＝vBt 竖直方向H＝gt2‎ 解得s≈1.41 m。‎ ‎(2)小球下摆到B点，轻绳的拉力和小球重力的合力提供向心力，由牛顿第二定律有F－mg＝m 解得F＝20 N 由牛顿第三定律得F′＝F＝20 N 即轻绳所受的最大拉力大小为20 N。‎ 答案　(1)1.41 m　(2)20 N 12‎