高中物理第八章气体第1节气体的等温变化导学案新人教版选修3-31 7页

1 气体的等温变化 内容 要求 等温变化 知道描述气体热学状态的参量及其物理意义，知道什么是等温变化，会 用等温变化的规律解释有关的物理现象。 玻意耳定律 掌握玻意耳定律的条件、内容、表达式，会用公式分析、计算有关问题； 理解气体等温变化的 p-V 图象。 在一个恒温池中，一串串气泡由池底慢慢升到水面，有趣的是气泡在上升过程中体积逐 渐增大，到达水面处破裂。同学们想一下，气泡在上升过程中体积为何会逐渐增大呢？ 提示：气泡在上升过程中可认为温度不变，由于在上升过程中压强不断变小，由玻意耳 定律可知，体积会逐渐变大。 一、等温变化 1．概念：一定____的气体，在____不变的条件下其压强与体积间发生的变化，叫做等 温变化。 2．实验探究 实验器材 铁架台、______、气压计等 研究对象 注射器内被封闭的一定质量的______ 数据收集 气体的压强由______读出，空气柱体积(长度)由______读出 数据处理 以______为纵坐标，以__________为横坐标，作出________图象 图象结果 p-1 V 图象是一条____________ 实验结论 一定质量的气体，在温度不变的条件下，其压强与__________成正比， 即压强与____成反比 思考 1：若实验数据呈现气体体积减小、压强增大的特点，能否断定压强与体积成反比？ 二、玻意耳定律 1．内容：一定____的某种气体，在____不变的情况下，压强 p 与体积 V 成____比。 2．公式：____＝C(常数)或 p1V1＝____(其中 p1、V1 和 p2、V2 分别表示气体在 1、2 两个 不同状态下的压强和体积)。 3．条件：气体的____一定，____不变。 三、气体等温变化的 p-V 图象 1．p-V 图象 一定质量的某种气体发生等温变化时的 p-V 图象为______的一支，如图所示。 2．p-1 V 图象 一定质量的某种气体发生等温变化时的 p-1 V 图象为延长线过____的________，如图所 示。 思考 2：如图所示有两条等温线，你能判断哪条等温线表示的温度比较高吗？为什么？ 答案：一、1.质量 温度 2．注射器 空气柱 气压计 刻度尺 压强 p 体积的倒数 p1 V 过原点的直线 体 积的倒数 体积 思考 1 提示：不能，也可能压强 p 与体积 V 的二次方(三次方)或与 V等成反比，只有作出 p 1 V 图象是直线，才能断定 p 与 V 成反比。 二、1.质量 温度 反 2．pV p2V2 3．质量 温度 三、1.双曲线 2．原点 倾斜直线 思考 2 提示：T2，因为它的 pV 乘积大。 一、封闭气体压强的计算 1．静止或匀速运动系统中封闭气体压强的确定 (1)液体封闭的气体的压强 ①平衡法：选与气体接触的液柱为研究对象，进行受力分析，利用它的受力平衡，求出 气体的压强。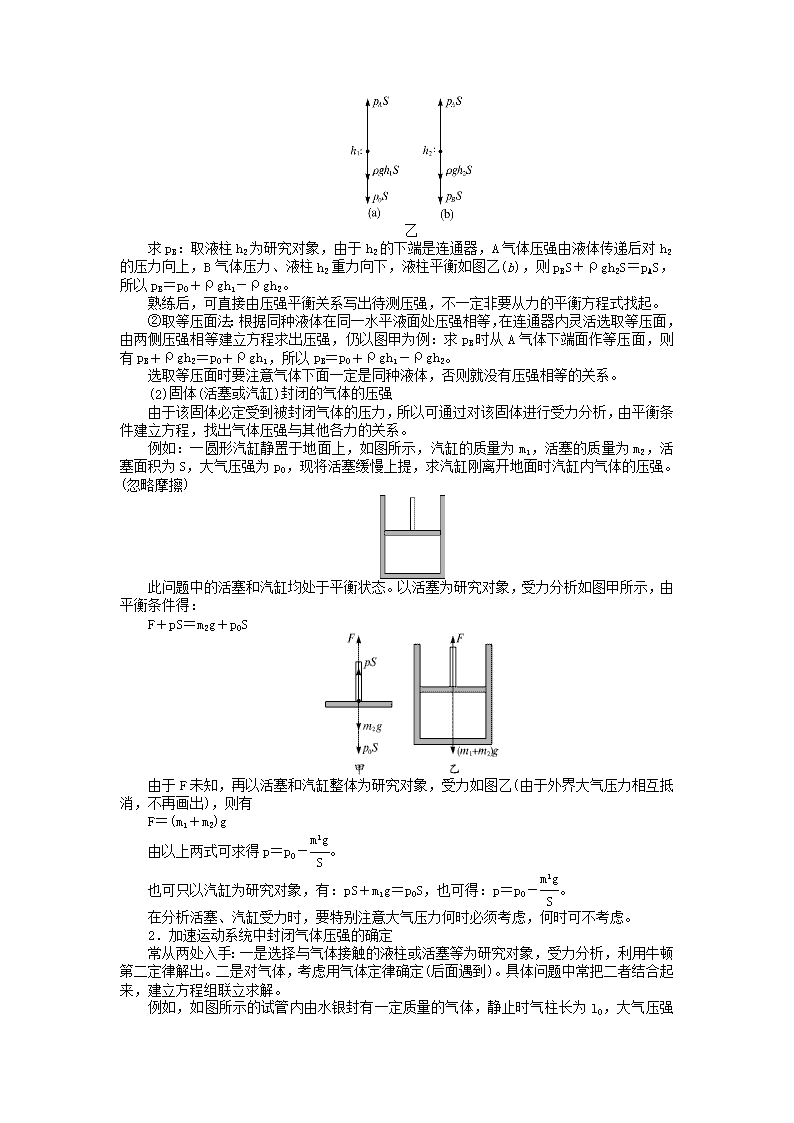 例如：在竖直放置的 U 形管内用密度为ρ的两部分液体封闭着两段空气柱。大气压强为 p0，各部分尺寸如图甲所示。求 A、B 气体的压强。 甲 求 pA：取液柱 h1 为研究对象，设管截面积为 S，大气压力和液柱重力向下，A 气体压力 向上，液柱 h1 静止，如图乙(a)，则 p0S＋ρgh1S＝pAS，所以 pA＝p0＋ρgh1。 乙 求 pB：取液柱 h2 为研究对象，由于 h2 的下端是连通器，A 气体压强由液体传递后对 h2 的压力向上，B 气体压力、液柱 h2 重力向下，液柱平衡如图乙(b)，则 pBS＋ρgh2S＝pAS，所 以 pB＝p0＋ρgh1－ρgh2。 熟练后，可直接由压强平衡关系写出待测压强，不一定非要从力的平衡方程式找起。 ②取等压面法：根据同种液体在同一水平液面处压强相等，在连通器内灵活选取等压面， 由两侧压强相等建立方程求出压强，仍以图甲为例：求 pB 时从 A 气体下端面作等压面，则 有 pB＋ρgh2＝p0＋ρgh1，所以 pB＝p0＋ρgh1－ρgh2。 选取等压面时要注意气体下面一定是同种液体，否则就没有压强相等的关系。 (2)固体(活塞或汽缸)封闭的气体的压强 由于该固体必定受到被封闭气体的压力，所以可通过对该固体进行受力分析，由平衡条 件建立方程，找出气体压强与其他各力的关系。 例如：一圆形汽缸静置于地面上，如图所示，汽缸的质量为 m1，活塞的质量为 m2，活塞 面积为 S，大气压强为 p0，现将活塞缓慢上提，求汽缸刚离开地面时汽缸内气体的压强。(忽 略摩擦) 此问题中的活塞和汽缸均处于平衡状态。以活塞为研究对象，受力分析如图甲所示，由 平衡条件得： F＋pS＝m2g＋p0S 由于 F 未知，再以活塞和汽缸整体为研究对象，受力如图乙(由于外界大气压力相互抵 消，不再画出)，则有 F＝(m1＋m2)g 由以上两式可求得 p＝p0－m1g S 。 也可只以汽缸为研究对象，有：pS＋m1g＝p0S，也可得：p＝p0－m1g S 。 在分析活塞、汽缸受力时，要特别注意大气压力何时必须考虑，何时可不考虑。 2．加速运动系统中封闭气体压强的确定 常从两处入手：一是选择与气体接触的液柱或活塞等为研究对象，受力分析，利用牛顿 第二定律解出。二是对气体，考虑用气体定律确定(后面遇到)。具体问题中常把二者结合起 来，建立方程组联立求解。 例如，如图所示的试管内由水银封有一定质量的气体，静止时气柱长为 l0，大气压强为 p0。当试管绕竖直轴以角速度ω在水平面内匀速转动时气柱长变为 l。其他尺寸如图所示。 求转动时的气体压强。(设温度不变，试管截面积为 S，水银密度为ρ) 选取水银柱为研究对象，转动所需向心力由液柱两侧气体压力差提供。 (p－p0)S＝mω2R 而 m＝ρl1S，R＝l2＋l1 2 所以 p＝p0＋ρl1ω2(l2＋l1 2 )。 (1)在考虑与气体接触的液柱所产生的附加压强 p＝ρgh 时，应特别注意 h 是表示液面 间的竖直高度，不一定是液柱长度。 (2)连通器原理：在连通器中，同一种液体(中间液体不间断)的同一水平液面上的压强 相等，如图中同一液面 C、D 处压强相等，则 pA＝p0＋ph。 二、对玻意耳定律的理解及应用 1．成立条件：玻意耳定律 p1V1＝p2V2 是实验定律。只有在气体质量一定、温度不变的条 件下才成立。 2．恒量的定义：p1V1＝p2V2＝恒量 C。 该恒量 C 与气体的种类、质量、温度有关，对一定质量的气体，温度越高，该恒量 C 越大。 3．两种等温变化图象 两种图象 内容 p- 1 V 图象 p-V 图象 图象特点 物理意义 一定质量的气体，温度不变时，pV＝恒量， p 与 V 成反比，p 与1 V 就成正比，在 p-1 V 图 上的等温线应是过原点的直线 一定质量的气体，在温度不变 的情况下 p 与 V 成反比，因此 等温过程的 p-V 图象是双曲线 的一支 温度高低 直线的斜率为 p 与 V 的乘积，斜率越大， pV 乘积越大，温度就越高，图中 T2＞T1 一定质量的气体，温度越高， 气体压强与体积的乘积必然越 大，在 p-V 图上的等温线就越 高，图中 T2＞T1 4.利用玻意耳定律解题的基本思路 (1)明确研究对象，根据题意确定所研究的是哪部分封闭气体，注意其质量和温度应不 变。 (2)明确状态参量，找准所研究气体初、末状态的 p、V 值。 (3)根据玻意耳定律列方程求解。 利用玻意耳定律解题时，经常使用 p1V1＝p2V2 或p1 p2 ＝V2 V1 这两种形式，单位要求使用同一单 位即可。 类型一 气体压强的计算 【例 1】 如图所示，一个横截面积为 S 的圆筒形容器竖直放置，金属圆板的上表面是水平的，下 表面是倾斜的，下表面与水平面的夹角为θ，圆板的质量为 m，不计圆板与容器内壁的摩擦。 若大气压强为 p0，则被圆板封闭在容器中的气体的压强等于( )。 A.p0＋mgcos θ S B. p0 cos θ ＋ mg Scos θ C．p0＋mgcos2θ S D．p0＋mg S 点拨：对封闭气体的圆板进行受力分析，然后根据平衡条件即可求出封闭气体的压强。 解析：为求气体的压强，应以封闭气体的圆板为研究对象，分析其受力，如图所示。由 物体的平衡条件得 p S cos θ ·cos θ＝p0S＋mg 解得：p＝p0＋mg S 所以正确选项为 D。 答案：D 题后反思：由本例题可以看出，当由液体或固体(活塞)封闭一部分气体，而且处于平衡 状态时，可以封闭气体的液体或固体为研究对象，分析其受力情况，画出受力图，由平衡条 件列出方程，从而求得气体压强。这是描述气体状态参量时经常采用的方法，应该熟练掌握。 触类旁通：若整体向上匀加速，加速度为 a，则封闭在容器中的气体的压强是多少？ 类型二 玻意耳定律的应用 【例 2】 粗细均匀的玻璃管内封闭一段长为 12 cm 的空气柱。一个人手持玻璃管开口 向下潜入水中，当潜到水下某深度时看到水进入玻璃管口 2 cm，求人潜入水中的深度。(玻 璃管内气体温度视为不变，取水面上大气压强为 p0＝1.0×105 Pa，g＝10 m/s2) 点拨：由于玻璃管内气体温度不变，被封闭气体的质量也不变，所以根据玻意耳定律问 题即可解决。 解析：确定研究对象为被封闭的一部分气体，玻璃管下潜的过程中气体的状态变化为等 温过程。 设潜入水下的深度为 h，玻璃管的横截面积为 S。气体的初末状态参量分别为 初状态：p1＝p0，V1＝12S。 末状态：p2＝p0＋ρgh，V2＝10S。 由玻意耳定律 p1V1＝p2V2，得 p0 p0＋ρgh ＝10S 12S 。 解得：h＝2 m。 答案：2 m 题后反思：应用玻意耳定律分析问题时要明确研究对象，确认温度不变，找准初、末状 态，分析并确定状态参量(p1，V1，p2，V2)，注意单位要统一，其中正确确定压强是运用玻意 耳定律的前提。 答案：触类旁通 答案：以活塞为研究对象，根据牛顿第二定律得 p S cos θ ·cos θ－p0S－mg＝ma 解得：p＝p0＋m(g＋a) S 。 1．有一段 12 cm 长的汞柱，在均匀玻璃管中封住一定质量的气体，若开口向上将玻璃 管放置在倾角为 30°的光滑斜面上，在下滑过程中被封气体的压强为(大气压强 p0＝76 cmHg)( )。 A．76 cmHg B．82 cmHg C．88 cmHg D．70 cmHg 2．(2010·广东理综)如图所示，某种自动洗衣机进水时，与洗衣缸相连的细管中会封 闭一定质量的空气，通过压力传感器感知管中的空气压力，从而控制进水量。设温度不变， 洗衣缸内水位升高，则细管中被封闭的空气( )。 A．体积不变，压强变小 B．体积变小，压强变大 C．体积不变，压强变大 D．体积变小，压强变小 3．如图所示为一定质量的气体在不同温度下的两条 p- 1 v 图线。由图可知( )。 A．一定质量的气体在发生等温变化时，其压强与体积成正比 B．一定质量的气体在发生等温变化时，其 p- 1 v 图线延长后经过坐标原点 C．T1＞T2 D．T1＜T2 4．如图所示，两端开口的均匀玻璃管竖直插入水银槽中，管中有一段水银柱 h1 封闭一 定质量的气体，这时管下端开口处内外水银面高度差为 h2，若保持环境温度不变，当外界压 强增大时，下列分析正确的是( )。 A．h2 变长 B．h2 变短 C．h1 上升 D．h1 下降 5．(2011·海南单科)如图，容积为 V1 的容器内充有压缩空气。容器与水银压强计相连， 压强计左右两管下部由软胶管相连，气阀关闭时，两管中水银面等高，左管中水银面上方到 气阀之间空气的体积为 V2。打开气阀，左管中水银面下降；缓慢地向上提右管，使左管中水 银面回到原来高度，此时右管与左管中水银面的高度差为 h。已知水银的密度为ρ，大气压 强为 p0，重力加速度为 g；空气可视为理想气体，其温度不变。求气阀打开前容器中压缩空 气的压强 p1。 答案：1.A 水银柱所处的状态不是平衡状态，因此不能用平衡条件来处理。水银柱的 受力分析如图所示，因玻璃管和水银柱组成系统的加速度 a=gsin θ，所以对水银柱，由牛 顿第二定律得： p0S+mgsin θ-pS=ma 故 p=p0。 2．B 水位升高，封闭气体体积减小，由玻意耳定律 pV＝C 可知压强变大，选项 B 正确。 3．BD 因为一定质量的气体温度不变时，pV＝C，所以其 p -1 V 图线延长后经过坐标原 点，所以 B 项正确；对同一部分气体来说，体积一定时，温度越高压强越大，所以 T2＞T1， D 项正确。 4．D 被封闭气体的压强为 p＝p0＋h1，或 p＝p0＋h2，始终有 h1＝h2；当 p0 增大时，被 封闭气体的压强增大，由玻意耳定律知，封闭气体的体积应减小。 5．解析：先选体积为 V2 的那部分气体为研究对象。其初状态的压强为 p0，末状态的压 强为(p0＋ρgh)，设末状态的体积为 V2′，由玻意耳定律得 p0V2＝(p0＋ρgh)V2′ 再研究容器内的压缩空气，其初状态的压强为 p1，体积为 V1；末状态的压强为 p0＋ρgh， 体积为(V1＋V2－V2′)。由玻意耳定律得 p1V1＝(p0＋ρgh)(V1＋V2－V2′) 联立两个方程解得 p1＝ 0 1 2 0 2 1 ( )( ) )p gh V V p V V ＋ ＋ － 。 答案： 0 1 2 0 2 1 ( )( ) )p gh V V p V V ＋ ＋ －