高中物理第三章万有引力定律3万有引力定律的应用课件-65张 65页

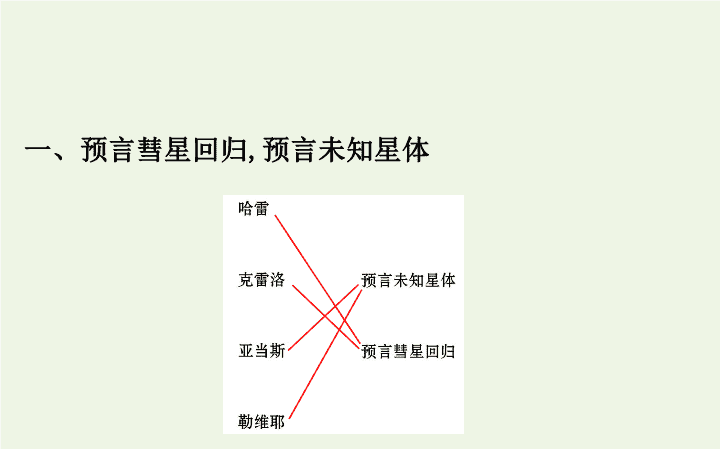
3.万有引力定律的应用 一、预言彗星回归 , 预言未知星体 二、计算天体的质量 【 思考 】 已知一个人的重力 , (1) 如何求出地球的质量 ? (2) 如何求地球的密度 ? 提示 : (1) 地面上物体的重力等于万有引力或卫星所受的万有引力等于向心力。 (2) 地球的质量除以地球的体积。 1. 地球质量的计算 : (1) 思路 : 地球表面的物体 , 忽略地球 _____ 影响 , 物体的 重力等于 _____________________ 。 (2) 关系式 :mg=_______ 。 自转 地球对物体的万有引力 (3) 结果 :M=____, 只要知道 g 、 R 、 G 的值 , 就可计算出 地球的质量。 2. 太阳质量的计算 : (1) 思路 : 绕中心天体运动的其他天体或卫星做 _____ _________, 向心力等于它与中心天体的万有引力 , 利 用此关系建立方程求中心天体的质量。 (2) 关系式 : 匀速 圆周运动 (3) 结论 :M=______, 只要知道了行星绕太阳运动的周期 T 和半径 r, 就可以计算出太阳的质量。 (4) 推广 : 若已知卫星绕行星运动的周期 T 和卫星与行星 之间的距离 r, 就可以计算行星的质量 M, 公式即 M= _______ 。 3. 其他行星的质量计算 : 若已知卫星绕行星的环绕周期 T 及环绕半径 r, 就可以计 算行星的质量 M=_______ 。 一　天体质量和密度的计算 任务 1 天体质量的计算 “ 自力更生法” “ 借助外援法” 情景 已知天体 ( 如地球 ) 的半径 R 和天体 ( 如地球 ) 表面的重力加速度 g 行星或卫星绕中心天体做匀速圆周运动 “ 自力更生法” “ 借助外援法” 思路 物体的重力近似等 于天体 ( 如地球 ) 与 物体间的万有引力 : 行星或卫星受到的万 有引力充当向心力 : “ 自力更生法” “ 借助外援法” 结果 天体 ( 如地球 ) 质量 : 中心天体质量 : 【 典例示范 1】 (2019· 遂宁高一检测 )2018 年 12 月 12 日 16 时 45 分 ,“ 嫦娥四号”成功实施近月制动 , 进入 环月轨道。如果“嫦娥四号”卫星在月球上空绕月球 做匀速圆周运动 , 经过时间 t, 卫星的路程为 s, 卫星与月 球球心连线转过的角度为 忽略月球的自转 , 万有引 力常量为 G 。试求月球的质量 M 。 【 解析 】 “ 嫦娥四号”的线速度、角速度分别为 又 v=ωr, 所以轨道半径为 根据万有引力提供向心力 解得 : 答案 : 任务 2 天体密度的计算 1. 一般思路 : 若天体半径为 R, 则天体的密度 将质量代入可求得密度。 2. 特殊情况 : 当卫星环绕天体表面运动时 , 其轨道半径 r 可认为等于天体半径 R, 依据 R=r, 可 得 : 【 思考 · 讨论 】 (1) 一卫星以 r 的半径绕质量为 M 的中心天体做周期为 T 的匀速圆周运动 , 如何求中心天体的质量 ? ( 模型建构 ) 提示 : (2) 在其他条件均不变的情况下 , 中心天体的密度越小 , 中心天体的半径越大 , 中心天体的半径能大于卫星的轨道半径 r 吗 ? ( 模型建构 ) 提示 : 不能 【 典例示范 2】 (2018· 全国卷 Ⅱ)2018 年 2 月 , 我国 500 m 口径射电望远镜 ( 天眼 ) 发现毫秒脉冲星 “ J0318+0253”, 其自转周期 T=5.19 ms 。假设星体为 质量均匀分布的球体 , 已知万有引力常量为 6.67× 10 -11 N·m 2 /kg 2 。以周期 T 稳定自转的星体的密度 最小值约为 【 解析 】 选 C 。星体自转的最小周期发生在其赤道上的 物质所受向心力正好全部由引力提供时 , 根据牛顿第二 定律 : 又因为 联立可得 ρ= ≈5×10 15 kg/m 3 , 选项 C 正确。 【 定向训练 】 1.( 多选 )(2018· 天津高考 )2018 年 2 月 2 日 , 我国成功将 电磁监测试验卫星“张衡一号”发射升空 , 标志我国成 为世界上少数拥有在轨运行高精度地球物理场探测卫 星的国家之一。通过观测可以得到卫星绕地球运动的 周期 , 并已知地球的半径和地球表面处的重力加速度。若将卫星绕地球的运动看作是匀速圆周运动 , 且不考虑地球自转的影响 , 根据以上数据可以计算出卫星的 ( 　　 ) A. 密度 B. 向心力的大小 C. 离地高度 D. 线速度的大小 【 解析 】 选 C 、 D 。根据题意 , 已知卫星运动的周期 T, 地 球的半径 R, 地球表面的重力加速度 g, 卫星受到的万有 引力充当向心力 , 故有 卫星的质量被消去 , 则不能计算卫星的密度 , 更不能计算卫星的向心力大 小 ,A 、 B 错误 ; 由 解得 而 r=R+h, 故可计算卫星距离地球表面的高度 ,C 正确 ; 根据 公式 , 轨道半径可以求出 , 周期已知 , 故可以计 算出卫星绕地球运动的线速度 ,D 正确。 2.(2019· 绵阳高一检测 ) 若嫦娥某型号探月卫星绕月球飞行 , 在靠近月球表面的圆轨道飞行时 , 绕行一周所用的时间为 T, 着陆月球后宇航员用弹簧秤测出质量为 m 的物体的重力为 F, 已知引力常量为 G 。求月球的半径和质量。 【 解析 】 设月球半径为 R, 月球质量为 M, 飞船质量为 m′ 月球表面的重力加速度为 月球表面万有引力等于重力 万有引力等于向心力 解得 : 答案 : 【 补偿训练 】 　　 1. 一个行星 , 其半径比地球的半径大 2 倍 , 质量是地球的 25 倍 , 则它表面的重力加速度是地球表面重力加速度的 ( 　　 ) A.6 倍　　　 B.4 倍　　　 C. 倍　　　 D.12 倍 【 解析 】 选 C 。根据 得 :g= , 因为行星 的质量是地球质量的 25 倍 , 半径是地球半径的 3 倍 , 则行 星表面的重力加速度是地球表面的重力加速度的 倍。故 C 正确 ,A 、 B 、 D 错误。 2.( 多选 ) 由下列哪一组物理量可以计算地球的质量 ( 　　 ) A. 月球的轨道半径和月球的公转周期 B. 月球的半径和月球的自转周期 C. 卫星的质量和卫星的周期 D. 卫星离地面的高度、卫星的周期和地球的半径 【 解析 】 选 A 、 D 。只要知道天体的一颗卫星或行星的 周期和轨道半径 , 利用公式 就可以计算出 中心天体的质量 , 故选项 A 、 D 正确。 二　天体运动的分析和计算 任务 1 天体运动的分析 1. 解决天体运动问题的基本思路 : 一般行星或卫星的运 动可看作匀速圆周运动 , 所需要的向心力都由中心天体 对它的万有引力提供 , 所以研究天体时可建立基本关系 式 : =ma, 式中 a 是向心加速度。 2. 常用的关系式 : (1) 万有引力全部用来提供行 星或卫星做圆周运动的向心力。 (2)mg= 即 gR 2 =GM, 物体在天体表面时受到的引力 等于物体的重力。该公式通常被称为黄金代换式。 3. 四个重要结论 : 设质量为 m 的天体绕另一质量为 M 的中 心天体做半径为 r 的匀速圆周运动。 (1) 由 r 越大 , 天体的 v 越小。 (2) 由 r 越大 , 天体的 ω 越小。 (3) 由 r 越大 , 天体的 T 越大。 (4) 由 r 越大 , 天体的 a n 越小。 以上结论可总结为“一定四定 , 越远越慢”。 【 思考 · 讨论 】 　情境 : 在电影 《 流浪地球 》 中 , 太阳即将毁灭 , 人类将要灭绝。为了人类的文明得以维系 , 流浪地球计划得以实施 , 刘培强等人连续在太空舱生活了 17 年。 讨论 :(1) 太空舱绕地球做圆周运动时 , 受力平衡吗 ? 什么力提供向心力 ? ( 科学思维 ) 提示 : 不平衡 , 万有引力 (2) 太空舱的运行周期是否可以求得 ? ( 科学思维 ) 提示 : 在知道中心天体质量和运动半径的情况下 , 可以利用万有引力的关系式求得运行周期。 【 典例示范 1】 (2019· 全国卷 Ⅲ) 金星、地球和火星绕太阳的公转均可视为匀速圆周运动 , 它们的向心加速度大小分别为 a 金 、 a 地 、 a 火 , 它们沿轨道运行的速率分别为 v 金 、 v 地 、 v 火 。已知它们的轨道半径 R 金 a 地 >a 火 B.a 火 >a 地 >a 金 C.v 地 >v 火 >v 金 D.v 火 >v 地 >v 金 【 解析 】 选 A 。由万有引力提供向心力 可知 轨道半径越小 , 向心加速度越大 , 故知 A 项正确 ,B 错误 ; 由 可知轨道半径越小 , 运行速率 越大 , 故 C 、 D 都错误。 任务 2 天体运动的计算 1. 比较围绕同一个中心天体做匀速圆周运动的行星或卫星的 v 、 ω 、 T 、 a n 等物理量的大小时 , 可考虑口诀“越远越慢” (v 、 ω 、 T) 、“越远越小” (a n ) 。 2. 涉及绕同一个中心天体做匀速圆周运动的行星或卫 星的计算问题时 , 若已知量或待求量中涉及重力加速度 g, 则应考虑黄金代换式 gR 2 =GM(mg= ) 的应用。 3. 若已知量或待求量中涉及 v 或 ω 或 T, 则应考虑从 中选择相应公式应用。 【 典例示范 2】 (2019· 攀枝花高一检测 ) 2018 年 5 月 4 日 凌晨 0 时 06 分，中国在西昌卫星发射中心用“长征三号 乙”运载火箭， 成功将亚太 6C 卫星送入东经 134 度的地 球同步轨道（卫星周期等于地球自转周期）。 ① 已知亚 太 6C 卫星轨道距地面高度为 h ，地球半径为 R ， ② 赤道上 物体随地球做圆周运动的加速度为 a ③ ，求亚太 6C 卫星在轨道上运行的周期和速度大小。 【 审题关键 】 序号 信息提取 ① 亚太 6C 卫星的周期为 24 小时 ② 卫星轨道半径为 h+R ③ 加速度 a 对应的半径为 R, 周期为 24 小时 【 解析 】 对赤道上随地球做圆周运动的物体 , 有 :a= ω 2 R, 同步卫星与赤道上的物体的周期都等于地球的自转 周期 , 得 : 对亚太 6C 卫星 , 有 : 答案 : 　 【 定向训练 】 1.2019 年是北斗系统加速组网的一年 , 完成组网后系统更稳定 , 分辨率更高。理论和实践表明 : 卫星离地面越近 , 分辨率就越高 , 那么分辨率越高的卫星 ( 　　 ) A. 线速度一定越小　　 B. 角速度一定越小 C. 周期一定越大 D. 向心加速度一定越大 【 解析 】 选 D 。根据万有引力提供向心力 =mω 2 r, 得 分辨率越高 ,r 越小 ,v 越大 , 故 A 错误 ; 角速度 分辨率越高 ,r 越小 ,ω 越大 , 故 B 错误 ; 分辨率越高 ,r 越小 ,T 越小 , 故 C 错 误 ; 分辨率越高 ,r 越小 ,a 越大 , 故 D 正确。 2.(2019· 资阳高一检测 ) 英国某媒体推测 : 在 2020 年 之前 , 人类有望登上火星 , 而登上火星的第一人很可能 是中国人。假如你有幸成为人类登陆火星的第一人 , 乘 坐我国自行研制的、代表世界领先水平的神舟 x 号宇宙 飞船 , 通过长途旅行 , 可以亲眼目睹美丽的火星。为了 熟悉火星的环境 , 你的飞船绕火星做匀速圆周运动 , 离火星表面的高度为 H, 飞行了 n 圈 , 测得所用的时间为 t 。已知火星半径为 R 、引力常量为 G 。 (1) 求火星表面重力加速度 g 。 (2) 求火星的平均密度 ρ 。 【 解析 】 (1) 设火星和飞船的质量分别为 M 、 m, 飞船绕 火星做匀速圆周运动的周期为 : 火星对飞船的万有引力提供飞船做匀速圆周运动的向 心力 对放在火星表面质量为 m 0 的物体有 : 联立得 : (2) 火星的质量为 火星半径为 R, 体积为 可以求得密度 答案 : (1) 　 (2) 【 补偿训练 】 　　 ( 多选 ) 假如一颗做匀速圆周运动的人造地球卫星 的轨道半径增大到原来的 2 倍 , 仍做匀速圆周运动 , 则 ( 　　 ) A. 根据公式 v=ωr, 可知卫星运动的线速度将增大到原来的 2 倍 B. 根据公式 F= 可知卫星所需的向心力将减少到原 来的 C. 根据公式 F= 可知地球提供的向心力将减少到 原来的 D. 根据上述 B 和 C 给出的公式 , 可知卫星运动的线速度将 减少到原来的 【 解析 】 选 C 、 D 。人造卫星绕地球运动时万有引力提 供向心力 , 即 F 向心 = 所以 当轨道半径 r 增加时 ,v 和 ω 都减小 , 故 A 错误 ; 由 可知 ,r 增大到原来的 2 倍时 , 向心力将减少 到原来的 , 选项 B 错误、 C 正确 ; 由 可知 , 当 r 增大 到原来的 2 倍时 , 线速度将减小到原来的 , 选项 D 正确。 【 课堂回眸 】