- 350.00 KB
- 2021-06-10 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
2.1.2 指数函数及其性质(一)
课时目标 1.理解指数函数的概念,会判断一个函数是否为指数函数.2.掌握指
数函数的图象和性质.
1.指数函数的概念
一般地,__________________叫做指数函数,其中 x 是自变量,函数的定义
域是____.
2.指数函数 y=ax(a>0,且 a≠1)的图象和性质
a>1 00 时,________;
当 x<0 时,________
当 x>0 时,________;
当 x<0 时,________
单调性 是 R 上的__________ 是 R 上的__________
一、选择题
1.下列以 x 为自变量的函数中,是指数函数的是( )
A.y=(-4)xB.y=πx
C.y=-4xD.y=ax+2(a>0 且 a≠1)
2.函数 f(x)=(a2-3a+3)ax 是指数函数,则有( )
A.a=1 或 a=2B.a=1
C.a=2D.a>0 且 a≠1
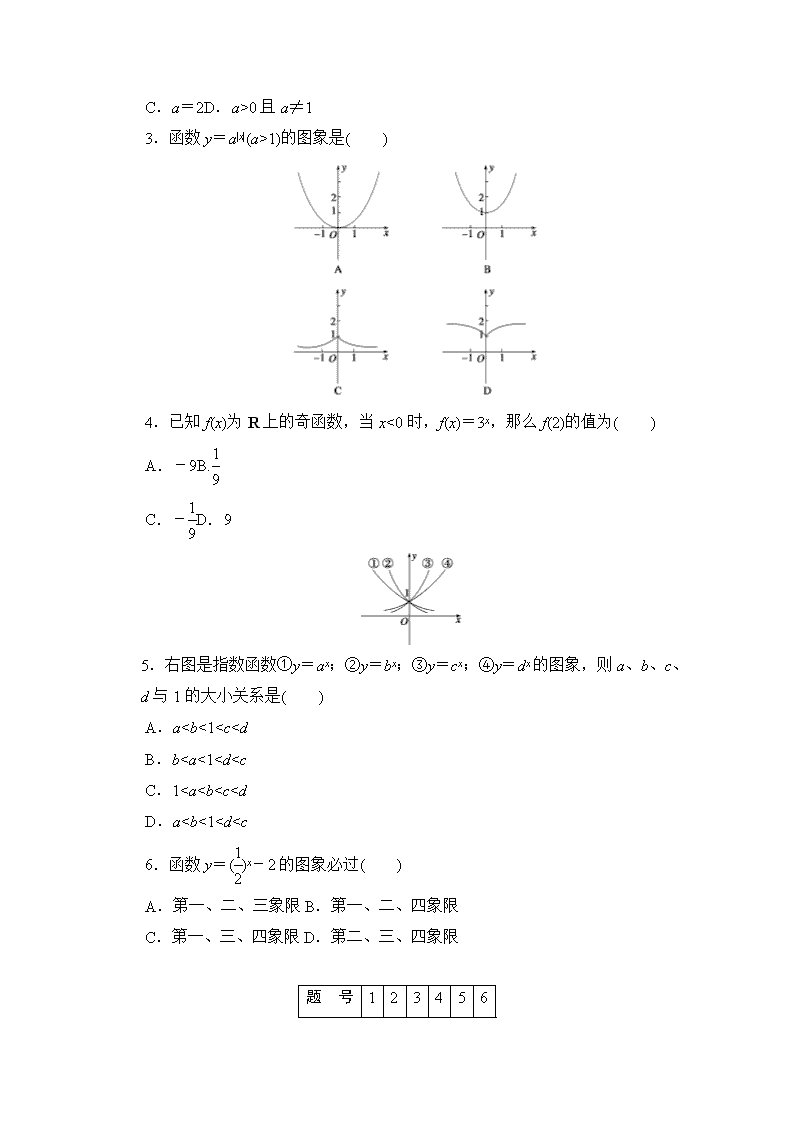
3.函数 y=a|x|(a>1)的图象是( )
4.已知 f(x)为 R 上的奇函数,当 x<0 时,f(x)=3x,那么 f(2)的值为( )
A.-9B.1
9
C.-1
9D.9
5.右图是指数函数①y=ax;②y=bx;③y=cx;④y=dx 的图象,则 a、b、c、
d 与 1 的大小关系是( )
A.a0,a≠1)的图象不经过第二象限,则 a,b 必满足
条件________________.
9.函数 y=8-23-x(x≥0)的值域是________.
三、解答题
10.比较下列各组数中两个值的大小:
(1)0.2-1.5 和 0.2-1.7;
(2)
1
31
4
和
2
31
4
;
(3)2-1.5 和 30.2.
11.2000 年 10 月 18 日,美国某城市的日报以醒目标题刊登了一条消息:“市
政委员会今天宣布:本市垃圾的体积达到 50000m3”,副标题是:“垃圾的体
积每三年增加一倍”.如果把 3 年作为垃圾体积加倍的周期,请你完成下面关
于垃圾的体积 V(m3)与垃圾体积的加倍的周期(3 年)数 n 的关系的表格,并回答
下列问题.
周期数 n 体积 V(m3)
0 50000×20
1 50000×2
2 50000×22
… …
n 50000×2n
(1)设想城市垃圾的体积每 3 年继续加倍,问 24 年后该市垃圾的体积是多少?
(2)根据报纸所述的信息,你估计 3 年前垃圾的体积是多少?
(3)如果 n=-2,这时的 n,V 表示什么信息?
(4)写出 n 与 V 的函数关系式,并画出函数图象(横轴取 n 轴).
(5)曲线可能与横轴相交吗?为什么?
能力提升
12.定义运算 a⊕b= aa≤b
ba>b
,则函数 f(x)=1⊕2x 的图象是( )
13.定义在区间(0,+∞)上的函数 f(x)满足对任意的实数 x,y 都有 f(xy)=yf(x).
(1)求 f(1)的值;
(2)若 f(1
2)>0,解不等式 f(ax)>0.(其中字母 a 为常数).
1.函数 y=f(x)与函数 y=f(-x)的图象关于 y 轴对称;函数 y=f(x)与函数 y=
-f(x)的图象关于 x 轴对称;函数 y=f(x)与函数 y=-f(-x)的图象关于原点对
称.
2.函数图象的平移变换是一种基本的图象变换.一般地,函数 y=f(x-a)的图
象可由函数 y=f(x)的图象向右(a>0)或向左(a<0)平移|a|个单位得到.
2.1.2 指数函数及其性质(一)
知识梳理
1.函数 y=ax(a>0,且 a≠1) R 2.(0,1) 0 1 y>1
01 增函数 减函数
作业设计
1.B [A 中-4<0,不满足指数函数底数的要求,C 中因有负号,也不是指数
函数,D 中的函数可化为 y=a2·ax,ax 的系数不是 1,故也不是指数函数.]
2.C [由题意得 a2-3a+3=1,
a>0 且 a≠1.
解得 a=2.]
3.B [该函数是偶函数.可先画出 x≥0 时,y=ax 的图象,然后沿 y 轴翻折过
去,便得到 x<0 时的函数图象.]
4.C [当 x>0 时,-x<0,∴f(-x)=3-x,
即-f(x)=(1
3)x,
∴f(x)=-(1
3)x.
因此有 f(2)=-(1
3)2=-1
9.]
5.B [作直线 x=1 与四个指数函数图象交点的坐标分别为(1,a)、(1,b)、(1,
c)、(1,d),由图象可知纵坐标的大小关系.]
6.D [函数 y=(1
2)x 的图象上所有的点向下平移 2 个单位,就得到函数 y=(1
2)x
-2 的图象,所以观察 y=(1
2)x-2 的图象知选 D.]
7.1
8
解析 由题意 a2=4,∴a=2.
f(-3)=2-3=1
8.
8.a>1,b≥2
解析 函数 y=ax-(b-1)的图象可以看作由函数 y=ax 的图象沿 y 轴平移|b-
1|个单位得到.若 01 时,由于 y=ax 的图象必过定点(0,1),当 y=ax 的图象
沿 y 轴向下平移 1 个单位后,得到的图象不经过第二象限.由 b-1≥1,得 b≥2.
因此,a,b 必满足条件 a>1,b≥2.
9.[0,8)
解析 y=8-23-x=8-23·2-x=8-8·(1
2)x
=8[1-(1
2)x].
∵x≥0,∴0<(1
2)x≤1,
∴-1≤-(1
2)x<0,
从而有 0≤1-(1
2)x<1,因此 0≤y<8.
10.解 (1)考查函数 y=0.2x.
因为 0<0.2<1,
所以函数 y=0.2x 在实数集 R 上是单调减函数.
又因为-1.5>-1.7,
所以 0.2-1.5<0.2-1.7.
(2)考查函数 y=(1
4)x.因为 0<1
4<1,
所以函数 y=(1
4)x 在实数集 R 上是单调减函数.
又因为1
3<2
3
,所以
(3)2-1.5<20,即 2-1.5<1;30<30.2,即 1<30.2,
所以 2-1.5<30.2.
11.解 (1)由于垃圾的体积每 3 年增加 1 倍,24 年后即 8 个周期后,该市垃
圾的体积是 50000×28=12800000(m3).
(2)根据报纸所述的信息,估计 3 年前垃圾的体积是 50000×2-1=25000(m3).
(3)如果 n=-2,这时的 n 表示 6 年前,V 表示 6 年前垃圾的体积.
(4)n 与 V 的函数关系式是 V=50000×2n,图象如图所示.
(5)因为对任意的整数 n,2n>0,所以 V=50000×2n>0,因此曲线不可能与横轴
相交.
12.A [由题意 f(x)=1⊕2x= 1, x≥0;
2x,x<0.
]
13.解 (1)令 x=1,y=2,可知 f(1)=2f(1),故 f(1)=0.
(2)设 0t,又 f(1
2)>0,
∴f(x1)-f(x2)=f[(1
2)s]-f[(1
2)t]
=sf(1
2)-tf(1
2)=(s-t)f(1
2)>0,
∴f(x1)>f(x2).
故 f(x)在(0,+∞)上是减函数.
又∵f(ax)>0,x>0,f(1)=0,
∴00 时,00 时,不等式解集为{x|0
相关文档
- 高中数学必背公式——立体几何与空2021-06-106页
- 2020高中数学 第二章 基本初等函数2021-06-104页
- 2012高中数学 3_2第4课时课时同步2021-06-106页
- 2020高中数学 第1章 立体几何初步 2021-06-105页
- 高中数学人教a版必修五第二章数列2021-06-106页
- 高中数学:新人教A版选修1-2 4_2结构2021-06-103页
- 人教a版高中数学选修1-1课时提升作2021-06-109页
- 高中数学 综合测试题1 新人教A版选2021-06-1013页
- 2020_2021学年高中数学第三章不等2021-06-1036页
- 2020年高中数学新教材同步必修第一2021-06-107页