- 1.73 MB
- 2021-06-10 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
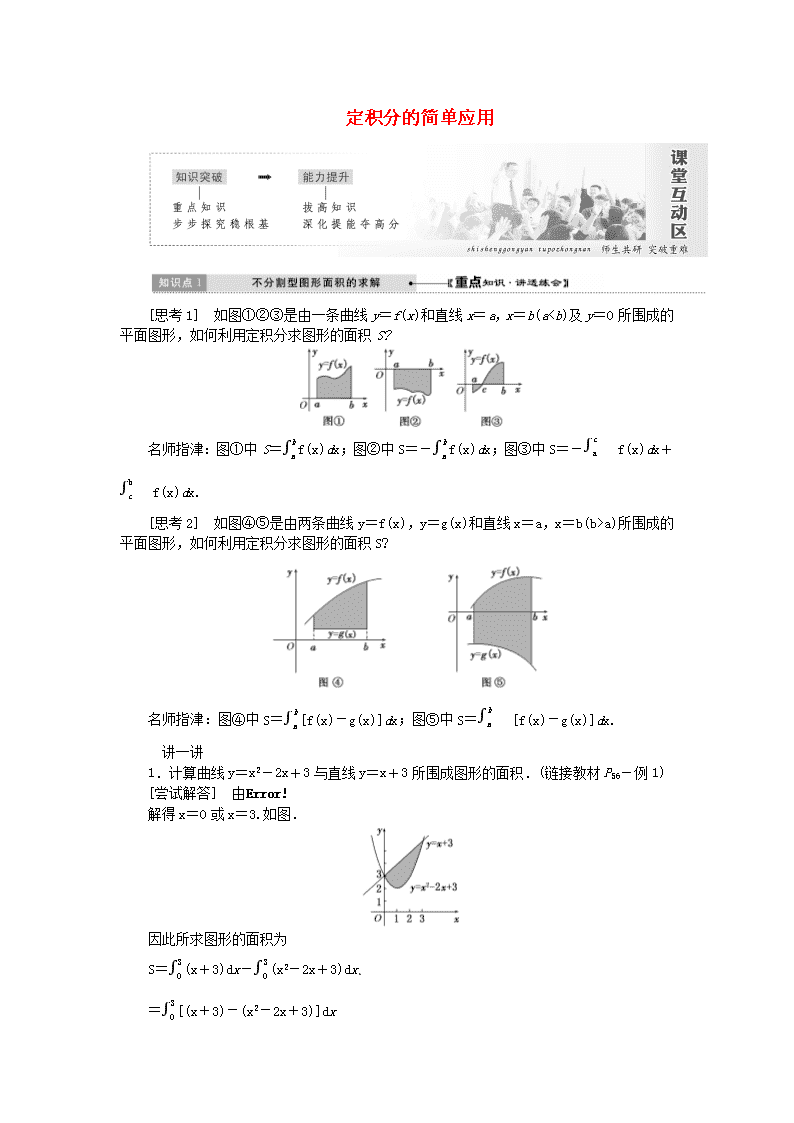
定积分的简单应用
[思考 1] 如图①②③是由一条曲线 y=f(x)和直线 x=a,x=b(aa)所围成的
平面图形,如何利用定积分求图形的面积 S?
名师指津:图④中 S=错误![f(x)-g(x)]dx;图⑤中 S=错误![f(x)-g(x)]dx.
讲一讲
1.计算曲线 y=x2-2x+3 与直线 y=x+3 所围成图形的面积.(链接教材 P56-例 1)
[尝试解答] 由
y=x+3,
y=x2-2x+3,
解得 x=0 或 x=3.如图.
因此所求图形的面积为
S=错误!(x+3)dx-错误!(x2-2x+3)dx
=错误![(x+3)-(x2-2x+3)]dx
=错误!(-x2+3x)dx
=
-1
3
x3+3
2
x2
3
0
=9
2
.
求不分割型图形面积的一般步骤如下:
同时,要注意被积函数是图形上边界对应的函数与下边界对应的函数的差.否则,有可
能得面积是负的.
练一练
1.求曲线 y=ex,y=e-x 及 x=1 所围成的图形面积.
解:
作图,并由
y=ex,
y=e-x,
解得交点(0,1).所求面积为错误!(ex-e-x)dx
=(ex+e-x)|1
0=e+1
e
-2.
[思考] 下图是由三条曲线 y=f(x)、y=g(x)和 y=h(x)围成的图形,且在[a,c]上,
f(x)≥g(x),在[c,b]上,f(x)≥h(x).
还能用[讲 1]的方法求该图形的面积吗?如果不能,该如何求解?
名师指津:不能.S=错误![f(x)-g(x)]dx+错误![f(x)-h(x)]dx.
讲一讲
2.(链接教材 P57-例 2)求曲线 y= x,y=2-x,y=-1
3
x 所围成的图形的面积.
[尝试解答] 画出草图,如图所示.
解方程组 y= x,
x+y=2,
y= x,
y=-1
3
x,
及
x+y=2,
y=-1
3
x, 得交点分别为(1,1),(0,0),(3,-1).
=错误!
x+1
3
x
dx+错误!
2-2
3
x
dx
=
2
3
x3
2
+1
6
x2
|1
0+
2x-1
3
x2
|3
1
=2
3
+1
6
+6-1
3
×9-2+1
3
=13
6
.
法二:若选y 为积分变量,则三个函数分别为 x=y2,
x=2-y,x=-3y.
因为它们的交点分别为(1,1),(0,0),(3,-1).
=-(-2+1)+2-1
2
-1
3
=13
6
.
由两条或两条以上的曲线围成的较为复杂的图形,在不同的区间内位于上方和下方的曲
线有所变化,通过解方程组求出曲线的不同的交点坐标,可以将积分区间进行细化分段,然
后对各个区间分别求面积进而求和,在每个区间上被积函数均是由上减下.若积分变量选取
x 运算较为复杂,可以选 y 为积分变量,被积函数改为 y 的函数,同时更改积分的上下限.
练一练
2.求曲线 xy=1 及直线 y=x,y=3 所围成图形的面积.
解:如图所示,由
xy=1,
y=x,
得 A 点坐标为(1,1);由
xy=1,
y=3,
得 B 点坐标为
1
3
,3
;
由
y=x,
y=3,
得 C 点坐标为(3,3).
法一:以 x 为积分变量,所求阴影部分的面积为
=2-ln 3+2
=4-ln 3.
法二:以 y 为积分变量,所求阴影部分的面积为
S=错误!
y-1
y dy=
1
2
y2-ln y |3
1
=4-ln 3.
[思考] 若做变速直线运动的物体的速度函数为 v=v(t)(v(t)≥0),则它在 t=a 到 t
=b(b>a)的时间段内所经过的路程 s 是多少?
提示:s=错误!v(t)dt.
讲一讲
3.(链接教材 P58-例 3)有一动点 P 沿 x 轴运动,在时间 t 时的速度为 v(t)=8t-2t2(速
度的正方向与 x 轴正方向一致).求:
(1)P 从原点出发,当 t=6 时,求点 P 移动的路程和离开原点的位移;
(2)P 从原点出发,经过时间 t 后又返回原点时的 t 值.
[尝试解答] (1)由 v(t)=8t-2t2≥0 得 0≤t≤4,
即当 0≤t≤4 时,P 点向 x 轴正方向运动,
当 t>4 时,P 点向 x 轴负方向运动.
故 t=6 时,点 P 移动的路 程
=
4t2-2
3
t3
|4
0-
4t2-2
3
t3
|6
4=128
3
.
当 t=6 时,点 P 的位移为
即 4t2-2
3
t3=0,
解得 t=0 或 t=6,
t=0 对应于 P 点刚开始从原点出发的情况,t=6 是从原点出发,又返回原点所用的时
间.
做变速直线运动的物体,从时刻 t=a 到时刻 t=b(a0 时,若 00,所以 a=2.
若 a>2,不符合题意.
综上,a=-1 或 2.
题组 2 分割型图形面积的求解
5.如图,阴影部分是由曲线 y=1
x
,y2=x 与直线 x=2,y=0 围成,则其面积为________.
解析:S=错误! xdx+错误!
1
x
dx
=2
3
+ln 2.
答案:2
3
+ln 2
6.求抛物线 y2=2x 和直线 y=-x+4 所围成的图形的面积.
解:先求抛物线和直线的交点,解方程组
y2=2x,
y=-x+4,
求出交点坐标为 A(2,2)和 B(8,-4).
法一:选x 为积分变量,变化区间为[0,8],将图形分割成两部分(如图),则面积为
S=S1+S2=2错误! 2xdx+错误!( 2x-x+4)dx
法二:选 y 作积分变量,则 y 的变化区间为[-4,2],如图得所求的面积为
=18.
题组 3 求变速直线运动的路程
7.一辆汽车以 v=3t2 的速度行驶,这辆汽车从 t=0 到 t=3 这段时间内所行驶的路程
为( )
错误! B.1 C.3 D.27
8.A、B 两站相距 7.2 km,一辆电车从 A 站开往 B 站,电车开出 t s 后到达途中 C 点,
这一段的速度为 m/s,到 C 点的速度为 24 m/s,从 C 点到 B 点前的 D 点以等速行驶,从 D
点开始刹车,速度为(24-m/s,经 t s 后,在 B 点恰好停车,试求:
(1)A、C 间的距离;
(2)B、D 间的距离.
解:(1)设 A 到 C 的时间为 t1,
则=24,t1=20 (s),
(2)设 D 到 B 的时间为 t2,
则 24-=0,t2=20(s),
则|DB|=∫20
0 (24-dt
=(24t-︱20
0 =240(m).
题组 4 求变力做功
9.做直线运动的质点在任意位置 x 处,所受力 F(x)=1+ex,则质点沿着与 F(x)相同
的方向,从点 x1=0 处运动到点 x2=1 处,力 F(x)所做的功是( )
A.1+e B.e
错误! D.e-1
解析:选 B W=错误!(1+ex)dx=(x+ex)︱1
0=e.
10.一物体在力 F(x)(单位:N)的作用下沿与力 F 相同的方向运动,力—位移曲线如图
所示.求该物体从 x=0 处运动到 x=4(单位:m)处力 F(x)做的功.
解:由力—位移曲线可知 F(x)=
10,0≤x≤2,
3x+4,2sin x.在
π
4
,5π
4 上,sin x>cos x.
8.已知函数 f(x)=ex-1,直线 l1:x=1,l2:y=et-1(t 为常数,且 0≤t≤1),直线
l1,l2 与函数 f(x)的图象围成的封闭图形,以及直线 l2,y 轴与函数 f(x)的图象围成的封闭
图形如图中阴影部分所示.求当 t 变化时,阴影部分的面积的最小值.
解:S1 +S2 =错误!(et -1-ex +1)dx+错误!(ex -1-et +1)dx=错误!(et -ex)dx+
错误!(ex-et)dx=(xet-ex)︱t
0+(ex-xet)︱1
t=(2t-3)et+e+1,取 g(t)=(2t-3)et+e+
1(0≤t≤1),令 g′(t)=0,解得 t=1
2
.当 t∈
0,1
2 时,g′(t)<0,g(t)是减函数;当
t∈
1
2
,1
时,g′(t)>0,g(t)是增函数,因此 g(t)的最小值为 g
1
2 =e+1-2e1
2
=( e-1)2.
故阴影部分面积的最小值为( e-1)2.
相关文档
- 2020_2021学年新教材高中数学第四2021-06-1043页
- 高中数学必修2教案:4_3_2 空间两点2021-06-102页
- 2020学年度高中数学 第一章 :第一课2021-06-104页
- 高中数学必修1课时作业与单元检测2021-06-107页
- 2020年高中数学第五章数系的扩充与2021-06-102页
- 2020高中数学函数的概念2021-06-106页
- 高中数学人教a版选修4-1课时跟踪检2021-06-105页
- 高中数学人教a版必修四课时训练:1.62021-06-106页
- 2019-2020学年高中数学课时作业122021-06-1010页
- 高中数学:3_1《直线的倾斜角与斜率2021-06-106页