高中数学人教a版必修四课时训练：1.6 三角函数模型的简单应用 6页

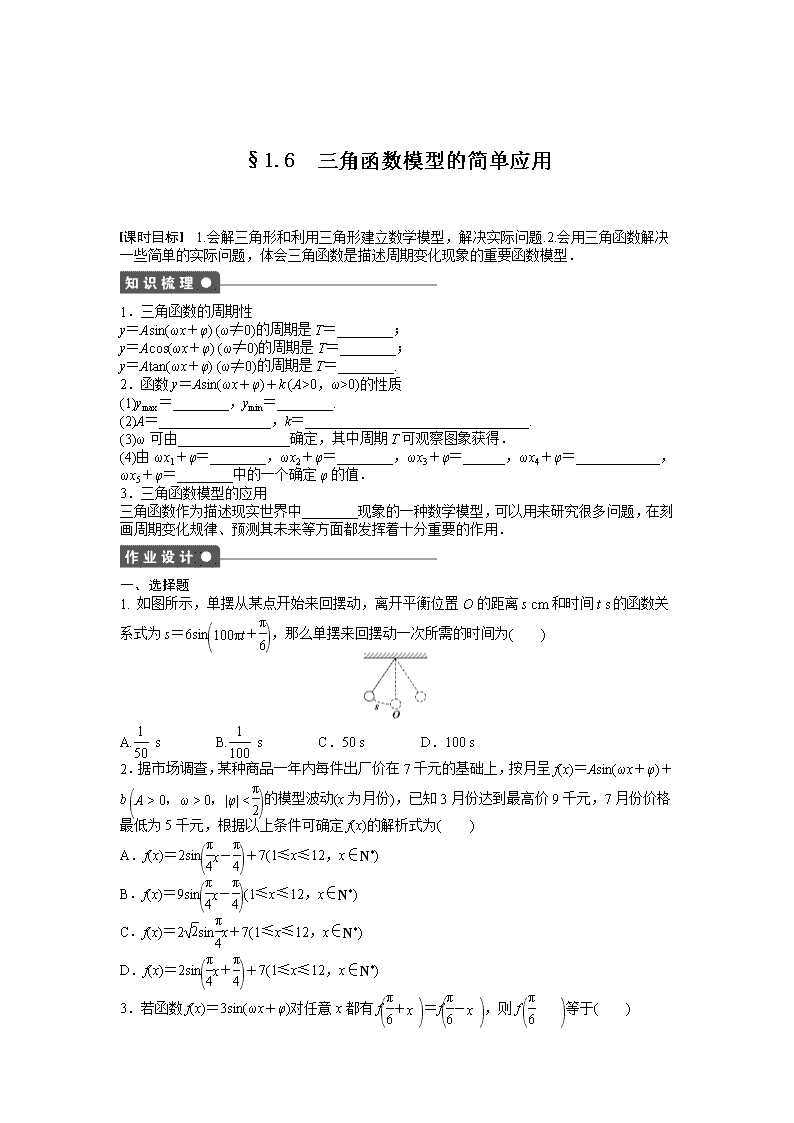
§1.6 三角函数模型的简单应用 课时目标 1.会解三角形和利用三角形建立数学模型，解决实际问题.2.会用三角函数解决 一些简单的实际问题，体会三角函数是描述周期变化现象的重要函数模型． 1．三角函数的周期性 y＝Asin(ωx＋φ) (ω≠0)的周期是 T＝________； y＝Acos(ωx＋φ) (ω≠0)的周期是 T＝________； y＝Atan(ωx＋φ) (ω≠0)的周期是 T＝________. 2．函数 y＝Asin(ωx＋φ)＋k (A>0，ω>0)的性质 (1)ymax＝________，ymin＝________. (2)A＝________________，k＝________________________________. (3)ω可由________________确定，其中周期 T 可观察图象获得． (4)由ωx1＋φ＝________，ωx2＋φ＝________，ωx3＋φ＝______，ωx4＋φ＝____________， ωx5＋φ＝________中的一个确定φ的值． 3．三角函数模型的应用 三角函数作为描述现实世界中________现象的一种数学模型，可以用来研究很多问题，在刻 画周期变化规律、预测其未来等方面都发挥着十分重要的作用． 一、选择题 1. 如图所示，单摆从某点开始来回摆动，离开平衡位置 O 的距离 s cm 和时间 t s 的函数关 系式为 s＝6sin 100πt＋π 6 ，那么单摆来回摆动一次所需的时间为( ) A. 1 50 s B. 1 100 s C．50 s D．100 s 2．据市场调查，某种商品一年内每件出厂价在 7 千元的基础上，按月呈 f(x)＝Asin(ωx＋φ) ＋b A>0，ω>0，|φ|<π 2 的模型波动(x 为月份)，已知 3 月份达到最高价 9 千元，7 月份价格 最低为 5 千元，根据以上条件可确定 f(x)的解析式为( ) A．f(x)＝2sin π 4x－π 4 ＋7(1≤x≤12，x∈N*) B．f(x)＝9sin π 4x－π 4 (1≤x≤12，x∈N*) C．f(x)＝2 2sinπ 4x＋7(1≤x≤12，x∈N*) D．f(x)＝2sin π 4x＋π 4 ＋7(1≤x≤12，x∈N*) 3．若函数 f(x)＝3sin(ωx＋φ)对任意 x 都有 f π 6 ＋x ＝f π 6 －x ，则 f π 6 等于( ) A．3 或 0 B．－3 或 0 C．0 D．－3 或 3 4. 如图所示，设点 A 是单位圆上的一定点，动点 P 从点 A 出发在圆上按逆时针方向旋转一 周，点 P 所旋转过的弧 AP 的长为 l，弦 AP 的长为 d，则函数 d＝f(l)的图象大致是( ) 5．设 y＝f(t)是某港口水的深度 y(米)关于时间 t(时)的函数，其中 0≤t≤24.下表是该港口某 一天从 0 时至 24 时记录的时间 t 与水深 y 的关系： t 0 3 6 9 12 15 18 21 24 y 12 15.1 12.1 9.1 11.9 14.9 11.9 8.9 12.1 经长期观察，函数 y＝f(t)的图象可以近似地看成函数 y＝k＋Asin(ωt＋φ)的图象．下面的函数 中，最能近似表示表中数据间对应关系的函数是( ) A．y＝12＋3sin π 6t，t∈[0,24] B．y＝12＋3sin π 6t＋π ，t∈[0,24] C．y＝12＋3sin π 12t，t∈[0,24] D．y＝12＋3sin π 12t＋π 2 ，t∈[0,24] 题 号 1 2 3 4 5 答 案 二、填空题 6．函数 y＝2sin m 3x＋π 3 的最小正周期在 2 3 ，3 4 内，则正整数 m 的值是________． 7．设某人的血压满足函数式 p(t)＝115＋25sin(160πt)，其中 p(t)为血压(mmHg)，t 为时间(min)， 则此人每分钟心跳的次数是________． 8．一根长 l cm 的线，一端固定，另一端悬挂一个小球，小球摆动时离开平衡位置的位移 s(cm) 与时间 t(s)的函数关系式时 s＝3cos g lt＋π 3 ，其中 g 是重力加速度，当小球摆动的周期是 1 s 时，线长 l 等于________． 三、解答题 9. 如图，一个水轮的半径为 4 m，水轮圆心 O 距离水面 2 m，已知水轮每分钟转动 5 圈，如 果当水轮上点 P 从水中浮现时(图中点 P0)开始计算时间． (1)将点 P 距离水面的高度 z(m)表示为时间 t(s)的函数； (2)点 P 第一次到达最高点大约需要多少时间？ 10．某港口水深 y(米)是时间 t (0≤t≤24，单位：小时)的函数，下面是水深数据： t(小时) 0 3 6 9 12 15 18 21 24 y(米) 10.0 13.0 9.9 7.0 10.0 13.0 10.1 7.0 10.0 据上述数据描成的曲线如图所示，经拟合，该曲线可近似的看成正弦函数型 y＝Asin ωt＋B 的图象． (1)试根据数据表和曲线，求出 y＝Asin ωt＋B 的解析式； (2)一般情况下，船舶航行时船底与海底的距离不小于 4.5 米是安全的，如果某船的吃水度(船 底与水面的距离)为 7 米，那么该船在什么时间段能够安全进港？若该船欲当天安全离港， 它在港内停留的时间最多不能超过多长时间？(忽略离港所用的时间) 能力提升 11．如图，质点 P 在半径为 2 的圆周上逆时针运动，其初始位置为 P0( 2，－ 2)，角速度 为 1，那么点 P 到 x 轴距离 d 关于时间 t 的函数图象大致为( ) 12．某时钟的秒针端点 A 到中心点 O 的距离为 5 cm，秒针均匀地绕点 O 旋转，当时间 t＝0 时，点 A 与钟面上标 12 的点 B 重合，将 A、B 两点的距离 d(cm)表示成 t(s)的函数，则 d＝ __________，其中 t∈[0,60]. 1．三角函数模型是研究周期现象最重要的数学模型．三角函数模型在研究物理、生物、自 然界中的周期现象(运动)有着广泛的应用． 2．三角函数模型构建的步骤 (1)收集数据，观察数据，发现是否具有周期性的重复现象． (2)制作散点图，选择函数模型进行拟合． (3)利用三角函数模型解决实际问题． (4)根据问题的实际意义，对答案的合理性进行检验． §1.6 三角函数模型的简单应用 答案 知识梳理 1.2π |ω| 2π |ω| π |ω| 2．(1)A＋k －A＋k (2)ymax－ymin 2 ymax＋ymin 2 (3)ω＝2π T (4)0 π 2 π 3 2π 2π 3．周期 作业设计 1．A 2.A 3．D [因为 f π 6 ＋x ＝f π 6 －x ，所以直线 x＝π 6 是函数 f(x)图象的对称轴．所以 f π 6 ＝ 3sin π 6ω＋φ ＝3sin kπ＋π 2 ＝±3.因此选 D.] 4．C [d＝f(l)＝2sin l 2.] 5．A [在给定的四个选项 A、B、C、D 中，我们不妨代入 t＝0 及 t＝3，容易看出最能近似 表示表中数据间对应关系的函数是 A.] 6．26,27,28 解析 ∵T＝6π m ，又∵2 3<6π m<3 4 ， ∴8π