2021届高考数学一轮复习第二章函数概念及基本初等函数Ⅰ第7节函数的图象课件新人教A版 48页

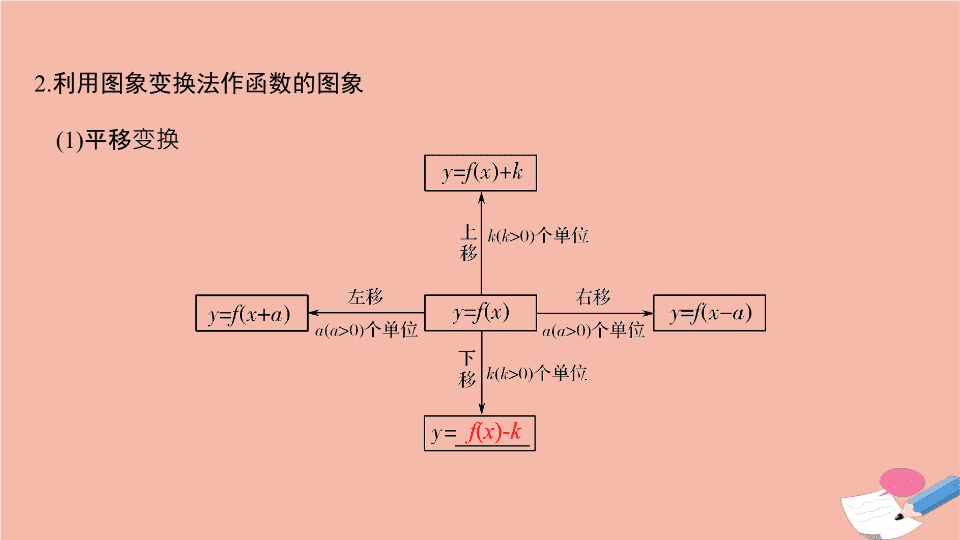
第 7 节　函数的图象 考试要求　 1. 在实际情境中，会根据不同的需要选择恰当的方法 ( 如图象法、列表法、解析法 ) 表示函数； 2. 会运用基本初等函数的图象分析函数的性质，解决方程解的个数与不等式解的问题 . 知 识 梳 理 1. 利用描点法作函数的图象 步骤： (1) 确定函数的定义域； (2) 化简函数解析式； (3) 讨论函数的性质 ( 奇偶性、单调性、周期性、对称性等 ) ； (4) 列表 ( 尤其注意特殊点、零点、最大值点、最小值点、与坐标轴的交点等 ) ，描点，连线 . 2. 利用图象变换法作函数的图象 (1) 平移变换 f ( x )- k － f ( x ) f ( － x ) － f ( － x ) log a x | f ( x )| f (| x |) [ 常用结论与微点提醒 ] 1. 记住几个重要结论 (1) 函数 y ＝ f ( x ) 与 y ＝ f (2 a － x ) 的图象关于直线 x ＝ a 对称 . (2) 函数 y ＝ f ( x ) 与 y ＝ 2 b － f (2 a － x ) 的图象关于点 ( a ， b ) 中心对称 . (3) 若函数 y ＝ f ( x ) 对定义域内任意自变量 x 满足： f ( a ＋ x ) ＝ f ( a － x ) ，则函数 y ＝ f ( x ) 的图象关于直线 x ＝ a 对称 . 2. 图象的左右平移仅仅是相对于 x 而言，如果 x 的系数不是 1 ，常需把系数提出来，再进行变换 . 3. 图象的上下平移仅仅是相对于 y 而言的，利用 “ 上减下加 ” 进行 . 诊 断 自 测 1. 判断下列结论正误 ( 在括号内打 “√” 或 “×” ) (1) 当 x ∈ (0 ，＋ ∞ ) 时，函数 y ＝ | f ( x )| 与 y ＝ f (| x |) 的图象相同 .( 　　 ) (2) 函数 y ＝ af ( x ) 与 y ＝ f ( ax )( a >0 且 a ≠ 1) 的图象相同 .( 　　 ) (3) 函数 y ＝ f ( x ) 与 y ＝－ f ( x ) 的图象关于原点对称 .( 　　 ) (4) 若函数 y ＝ f ( x ) 满足 f (1 ＋ x ) ＝ f (1 － x ) ，则函数 f ( x ) 的图象关于直线 x ＝ 1 对称 .( 　　 ) 解析　 (1) 令 f ( x ) ＝－ x ，当 x ∈ (0 ，＋ ∞ ) 时， y ＝ | f ( x )| ＝ x ， y ＝ f (| x |) ＝－ x ，两者图象不同， (1) 错 . (2) 中两函数当 a ≠ 1 时， y ＝ af ( x ) 与 y ＝ f ( ax ) 是由 y ＝ f ( x ) 分别进行振幅与周期变换得到，两图象不同， (2) 错 . (3) y ＝ f ( x ) 与 y ＝－ f ( x ) 图象关于 x 轴对称， (3) 错 . (4) 中， f (2 － x ) ＝ f [1 ＋ (1 － x )] ＝ f [1 － (1 － x )] ＝ f ( x ) ，所以 y ＝ f ( x ) 的图象关于直线 x ＝ 1 对称， (4) 正确 . 答案　 (1) × 　 (2) × 　 (3) × 　 (4) √ 解析 　其图象是由 y ＝ x 2 图象中 x <0 的部分和 y ＝ x － 1 图象中 x ≥ 0 的部分组成 . 答案 　 C 3. ( 新教材必修第一册 P140 习题 4.4T6) 在 2 h 内将某种药物注射进患者的血液中，在注射期间，血液中的药物含量呈线性增加；停止注射后，血液中的药物含量呈指数衰减，能反映血液中药物含量 Q 随时间 t 变化的图象是 ( 　　 ) 解析　 依题意，在 2 h 内血液中药物含量 Q 持续增加，停止注射后， Q 呈指数衰减，图象 B 适合 . 答案　 B 4. ( 一题多解 )(2018· 全国 Ⅲ 卷 ) 下列函数中，其图象与函数 y ＝ ln x 的图象关于直线 x ＝ 1 对称的是 ( 　　 ) A. y ＝ ln(1 － x ) B. y ＝ ln(2 － x ) C. y ＝ ln(1 ＋ x ) D. y ＝ ln(2 ＋ x ) 解析　法一　 设所求函数图象上任一点的坐标为 ( x ， y ) ，则其关于直线 x ＝ 1 的对称点的坐标为 (2 － x ， y ) ，由对称性知点 (2 － x ， y ) 在函数 f ( x ) ＝ ln x 的图象上，所以 y ＝ ln(2 － x ). 法二　 由题意知，对称轴上的点 (1 ， 0) 在函数 y ＝ ln x 的图象上也在所求函数的图象上，代入选项中的函数表达式逐一检验，排除 A ， C ， D ，选 B. 答案　 B ∴ f ( x ) 为奇函数，排除 A. 答案　 D 答案　 (2 ， 8] 考点一　作函数的图象 【例 1 】 作出下列函数的图象： (2) 将函数 y ＝ log 2 x 的图象向左平移一个单位，再将 x 轴下方的部分沿 x 轴翻折上去，即可得到函数 y ＝ |log 2 ( x ＋ 1)| 的图象，如图 ② . 规律方法　 作函数图象的一般方法 (1) 直接法 . 当函数解析式 ( 或变形后的解析式 ) 是熟悉的基本函数时，就可根据这些函数的特征描出图象的关键点直接作出 . (2) 图象变换法 . 若函数图象可由某个基本函数的图象经过平移、翻折、对称得到，可利用图象变换作出，并应注意平移变换与伸缩变换的顺序对变换单位及解析式的影响 . 【训练 1 】 分别作出下列函数的图象： (1) y ＝ |lg x | ； (2) y ＝ sin | x |. 解　 (1) 先作出函数 y ＝ lg x 的图象，再将 x 轴下方的部分沿 x 轴翻折上去，即可得函数 y ＝ |lg x | 的图象，如图 ① 实线部分 . (2) 当 x ≥ 0 时， y ＝ sin| x | 与 y ＝ sin x 的图象完全相同，又 y ＝ sin| x | 为偶函数，图象关于 y 轴对称，其图象如图 ② . 考点二　函数图象的辨识 所以 f ( x ) 是奇函数，排除选项 C. 所以 f ( x ) 的定义域为 ( － 1 ， 0) ∪ (0 ， 1) ，关于原点对称 . 又 f ( x ) ＝ f ( － x ) ，所以函数 f ( x ) 是偶函数，图象关于 y 轴对称，排除 A ； 当 0< x <1 时， lg | x |<0 ， f ( x )<0 ，排除 C ； 当 x >0 且 x → 0 时， f ( x ) → 0 ，排除 D ，只有 B 项符合 . 答案　 (1)B 　 (2)B 规律方法　 1. 抓住函数的性质，定性分析： (1) 从函数的定义域，判断图象的左右位置；从函数的值域，判断图象的上下位置； (2) 从函数的单调性，判断图象的变化趋势； (3) 从周期性，判断图象的循环往复； (4) 从函数的奇偶性，判断图象的对称性 . 2. 抓住函数的特征，定量计算： 从函数的特征点，利用特征点、特殊值的计算分析解决问题 . 法二　 当 x ＝ 1 时， f (1) ＝ 1 ＋ 1 ＋ sin 1 ＝ 2 ＋ sin 1>2 ，排除 A ， C ；又当 x → ＋ ∞ 时， y → ＋ ∞ ，排除 B ，而 D 满足 . 答案　 (1)B 　 (2)D 考点三　函数图象的应用　 多维探究 角度 1 　研究函数的性质 【例 3 － 1 】 已知函数 f ( x ) ＝ x | x | － 2 x ，则下列结论正确的是 ( 　　 ) A. f ( x ) 是偶函数，递增区间是 (0 ，＋ ∞ ) B. f ( x ) 是偶函数，递减区间是 ( － ∞ ， 1) C. f ( x ) 是奇函数，递减区间是 ( － 1 ， 1) D. f ( x ) 是奇函数，递增区间是 ( － ∞ ， 0) 答案　 C 角度 2 　函数图象在不等式中的应用 【例 3 － 2 】 (1) (2020· 哈尔滨模拟 ) 已知函数 f ( x ) ＝ 2 － | x | ，若关于 x 的不等式 f ( x ) ≥ x 2 － x － m 的解集中有且仅有 1 个整数，则实数 m 的取值范围为 ( 　　 ) A.[ － 3 ，－ 1) B.( － 3 ，－ 1) C.[ － 2 ，－ 1) D.( － 2 ，－ 1) 解析　 (1) 在同一平面直角坐标系中作出函数 y ＝ f ( x ) ， y ＝ x 2 － x － m 的图象如图所示 . 由图可知，不等式 f ( x ) ≥ x 2 － x － m 的解集中的整数解为 x ＝ 0 ， 角度 3 　求参数的取值范围 【例 3 － 3 】 设函数 f ( x ) ＝ | x 2 － 2 x | － ax － a ，其中 a >0 ，若只存在两个整数 x ，使得 f ( x )<0 ，则 a 的取值范围是 ______. 解析　 f ( x ) ＝ | x 2 － 2 x | － ax － a <0 ，则 | x 2 － 2 x |< ax ＋ a ， 分别画出 y ＝ | x 2 － 2 x | 与 y ＝ a ( x ＋ 1) 的图象，如图所示 . ∵ 只存在两个整数 x ，使得 f ( x )<0 ， 当 x ＝ 1 时， |1 2 － 2| ＝ 1 ，令 2 a ＝ 1 ， 规律方法　 1. 利用函数的图象研究函数的性质 对于已知或易画出其在给定区间上图象的函数，其性质 ( 单调性、奇偶性、周期性、最值 ( 值域 ) 、零点 ) 常借助于图象研究，但一定要注意性质与图象特征的对应关系 . 2. 利用函数的图象可解决某些方程和不等式的求解问题，方程 f ( x ) ＝ g ( x ) 的根就是函数 f ( x ) 与 g ( x ) 图象交点的横坐标；不等式 f ( x )< g ( x ) 的解集是函数 f ( x ) 的图象位于 g ( x ) 图象下方的点的横坐标的集合，体现了数形结合思想 . A. 函数 f ( x ) 的图象关于点 (1 ， 0) 中心对称 B. 函数 f ( x ) 在 ( － ∞ ， 1) 上是增函数 C. 函数 f ( x ) 的图象关于直线 x ＝ 1 对称 D. 函数 f ( x ) 的图象上至少存在两点 A ， B ，使得直线 AB ∥ x 轴 (2) ( 角度 2) 已知函数 y ＝ f ( x ) 的图象是如图所示的折线 ACB ，且函数 g ( x ) ＝ log 2 ( x ＋ 1) ，则不等式 f ( x ) ≥ g ( x ) 的解集是 ( 　　 ) A.{ x | － 1< x ≤ 0} B.{ x | － 1 ≤ x ≤ 1} C.{ x | － 1< x ≤ 1} D.{ x | － 1< x ≤ 2} (2) 令 g ( x ) ＝ y ＝ log 2 ( x ＋ 1) ，作出函数 g ( x ) 的图象如图， ∴ 结合图象知不等式 f ( x ) ≥ log 2 ( x ＋ 1) 的解集为 { x | － 1< x ≤ 1}. 答案　 (1)A 　 (2)C 　 (3)B 直观想象 —— 函数图象的活用 直观想象是发现和提出问题，分析和解决问题的重要手段，在数学研究的探索中，通过直观手段的运用以及借助直观展开想象，从而发现问题、解决问题的例子比比皆是，并贯穿于数学研究过程的始终，而数形结合思想是典型的直观想象范例 . 类型 1 　根据函数图象特征，确定函数解析式 函数解析式与函数图象是函数的两种重要表示法，图象形象直观，解析式易于研究函数性质，可根据需要，相互转化 . 【例 1 】 (2020· 长沙模拟 ) 如图，已知函数 f ( x ) 的图象关于坐标原点对称，则函数 f ( x ) 的解析式可能是 ( 　　 ) 答案　 C 类型 2 　利用函数的图象研究函数的性质 对于已知或易画出其在给定区间上图象的函数，其性质 ( 单调性、奇偶性、周期性、最值 ( 值域 ) 、零点 ) 常借助图象研究，但一定要注意性质与图象特征的对应关系 . 【例 2 】 已知 f ( x ) ＝ 2 x － 1 ， g ( x ) ＝ 1 － x 2 ，规定：当 | f ( x )| ≥ g ( x ) 时， h ( x ) ＝ | f ( x )| ；当 | f ( x )| ＜ g ( x ) 时， h ( x ) ＝－ g ( x ) ，则 h ( x )( 　　 ) A. 有最小值－ 1 ，最大值 1 B. 有最大值 1 ，无最小值 C. 有最小值－ 1 ，无最大值 D. 有最大值－ 1 ，无最小值 解析　 画出 y ＝ | f ( x )| ＝ |2 x － 1| 与 y ＝ g ( x ) ＝ 1 － x 2 的图象，它们交于 A ， B 两点 . 由 “ 规定 ” ，在 A ， B 两侧， | f ( x )| ≥ g ( x ) ，故 h ( x ) ＝ | f ( x )| ；在 A ， B 之间， | f ( x )|< g ( x ) ，故 h ( x ) ＝－ g ( x ). 综上可知， y ＝ h ( x ) 的图象是图中的实线部分，因此 h ( x ) 有最小值－ 1 ，无最大值 . 答案　 C A.5 B.6 C.7 D.8 答案　 C 思维升华　 求解图象交点横、纵坐标之和的问题，常利用图象的对称性求解，即找出两图象的公共对称轴或对称中心，从而得出各交点的公共对称轴或对称中心，由此得出定值求解 . 类型 3 　利用函数的图象求解方程或不等式 若研究的方程 ( 不等式 ) 不能用代数法求解，但其与基本初等函数有关，常将方程 ( 不等式 ) 问题转化为两函数图象的交点或图象的上下位置关系，然后由图象的几何直观数形结合求解 . 解析　 f ( x ) ＝ 2sin x cos x － x 2 ＝ sin 2 x － x 2 ，函数 f ( x ) 的零点个数可转化为函数 y 1 ＝ sin 2 x 与 y 2 ＝ x 2 图象的交点个数，在同一坐标系中画出 y 1 ＝ sin 2 x 与 y 2 ＝ x 2 的图象如图所示： 由图可知两函数图象有 2 个交点，则 f ( x ) 的零点个数为 2. 答案　 2