- 957.98 KB
- 2021-06-10 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
第六章 数列
二、重难点击
本章重点:数列的概念,等差数列,等比数列的定义,通项公式和前 n 项和公式及运用,等差数列、等比数
列的有关性质。注重提炼一些重要的思想和方法,如:观察法、累加法、累乘法、待定系数法、倒序相加求
和法、错位相减求和法、裂项相消求和法、函数与方程思想、分类与讨论思想、化归与转化思想等。
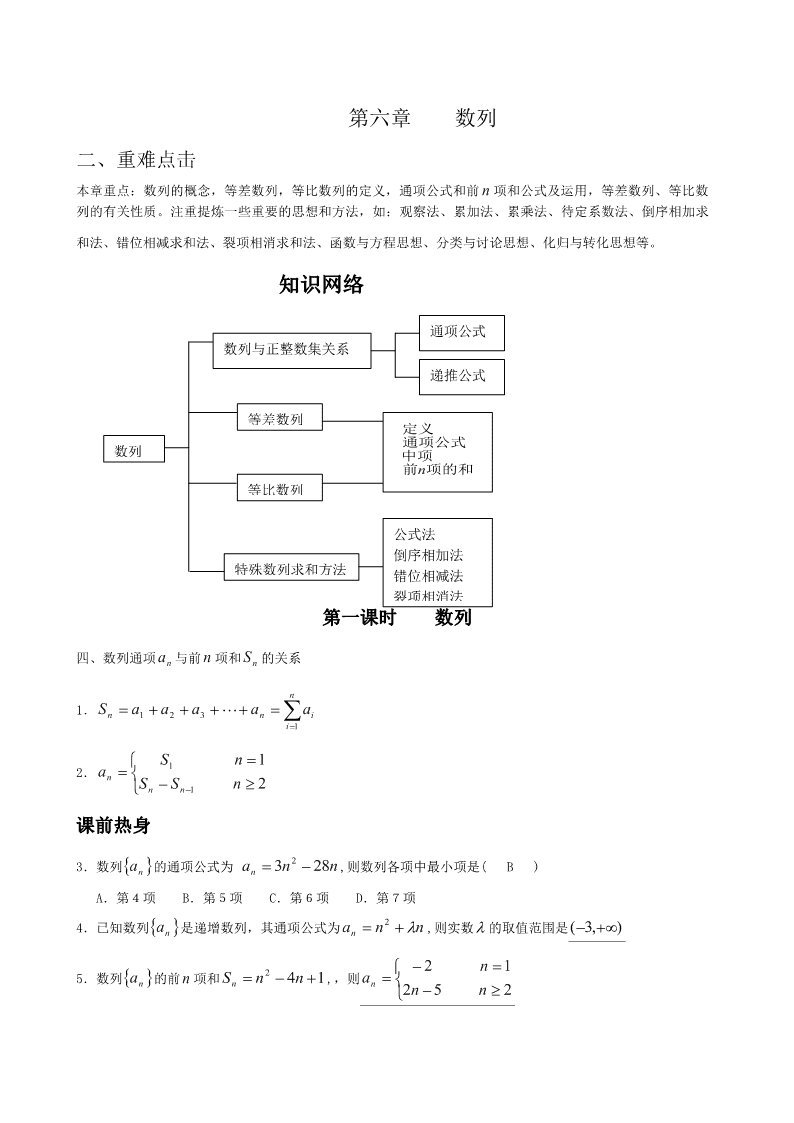
知识网络
第一课时 数列
四、数列通项 na 与前 n 项和 nS 的关系
1.
n
i
inn aaaaaS
1
321
2.
2
1
1
1
nSS
nSa
nn
n
课前热身
3.数列 na 的通项公式为 nnan 283 2 ,则数列各项中最小项是( B )
A.第4项 B.第5项 C.第6项 D.第7项
4.已知数列 na 是递增数列,其通项公式为 nnan 2 ,则实数 的取值范围是 ),3(
5.数列 的前 项和 142 nnSn ,,则
252
12
nn
nan
数列与正整数集关系
等差数列
等比数列
特殊数列求和方法
公式法
倒序相加法
错位相减法
裂项相消法
n
定义
通项公式
中项
前 项的和
递推公式
通项公式
数列
题型一 归纳、猜想法求数列通项
【例 1】根据下列数列的前几项,分别写出它们的一个通项公式
⑴7,77,777,7777,…
⑶1,3,3,5,5,7,7,9,9…
解析:⑴将数列变形为 ),110(9
7 ),110(9
7 2 )110(9
7 3 , , )110(9
7 n
⑶将已知数列变为 1+0,2+1,3+0,4+1,5+0,6+1,7+0,8+1,9+0,…。可得数列的通项公式为
2
)1(1 n
n na
点拨:本例的求解关键是通过分析、比较、联想、归纳、转换获得项与项数的一般规律,从而求得通项。
题型二 应用
)2(
)1(
1
1
nSS
nSa
nn
n 求数列通项
例 2.已知数列 na 的前 n 项和 nS ,分别求其通项公式.
⑴ 23 n
nS
解析:⑴当 123,1 1
11 San 时 ,
当 )23()23(,2 1
1
nn
nnn SSan 时
132 n
又 11 a 不适合上式,故
)2(32
)1(1
1 n
na nn
三、利用递推关系求数列的通项
【例 3】根据下列各个数列 的首项和递推关系,求其通项公式
⑴
14
1,2
1
211 naaa nn
解析:⑴因为
14
1
21 naa nn ,所以
)12
1
12
1(2
1
14
1
21 nnnaa nn
所以 )3
1
1
1(2
1
12 aa
)5
1
3
1(2
1
23 aa
43
1 1 1()2 5 7aa
…,…,
1
1 1 1()2 2 3 2 1nnaa nn
以上 )1( n 个式相加得
)12
11(2
1
1 naan
即:
24
34
24
11
n
n
nan
点 拨 : 在 递 推 关 系中若 ),(1 nfaa nn 求 na 用 累 加 法 , 若 ),(1 nfa
a
n
n 求 na 用 累 乘 法 , 若
qpaa nn 1 ,求 用待定系数法或迭代法。
课外练习
3 设
12
1
2
1
1
1
nnnan ,( Nn ),则 nn aa 与1 的大小关系是( C )
A. nn aa 1 B. nn aa 1
C. nn aa 1 D.不能确定
解:因为
022
1
32
1
1
1
32
1
22
1
1
nn
nnnaa nn
所以 ,选C.
二、填空题
5.已知数列 na 的前 n 项和 ,142 nnSn 则
)2(,52
)1(,2
nn
nan
7.已知数列 的通项
99
98
n
n ( ),则数列 的前 30 项中最大项和最小项分别是 910 aa ,
解:构造函数
99
98991
99
98
xx
xy
由函数性质可知,函数在 )99( , 上递减,且 1y
函数在 ),+99( 上递增且 1y
最小最大,
),又
910
9
2130121110 1
109(99
aa
a
aaaaaa
三、解答题
6.2 等差数列
知识要点
2.递推关系与通项公式
mn
aad
n
aad
dnaa
dmnaa
dnaa
daa
mn
n
n
mn
n
nn
1
;)1(
)(
)1(
1
1
1
1
变式:
推广:
通项公式:
递推关系:
为常数)即:
特征:
mkmknnfa
dadna
n
n
,(,)(
),( 1
), 为常数,( mkmknan 是数列 na 成
等差数列的充要条件。
3.等差中项:
若 cba ,, 成等差数列,则 b 称 ca与 的等差中项,
且
2
cab ; cba ,, 成等差数列是 cab 2 的充
要条件。
4.前 n 项和公式
2
)( 1 naaS n
n
;
2
)1(
1
dnnnaSn
),(
)(
,)2(2
2
2
1
2
为常数
即
特征:
BABnAnS
BnAnnfS
ndandS
n
n
n
是数列 成等差数列的充要条件。
5.等差数列 的基本性质 ),,,( Nqpnm其中
⑴ qpnm aaaaqpnm ,则若 反
之,不成立。
⑵ dmnaa mn )(
⑶ mnmnn aaa 2
⑷ nnnnn SSSSS 232 ,, 仍成等差数列。
6.判断或证明一个数列是等差数列的方法:
①定义法:
)常数)(
Nndaa nn (1 是等
差数列
②中项法:
)2 21
Nnaaa nnn ( 是等差数
列
③通项公式法:
),( 为常数bkbknan 是等差数
列
④前 项和公式法:
),(2 为常数BABnAnSn 是等
差数列
课前热身
2.等差数列 中,
)(3
1
,120
119
1210864
Caa
aaaaa
的值为则
A.14 B.15 C.16 D.17
165
120
3
2
3
2)(3
2
)2(3
1
3
1
89
99119
ada
daaaa
解
。
3.等差数列 na 中, 1291 0 SSa , ,则前 10
或 11 项的和最大。
解: 0912129 SSSS ,
00
030
111
11121110
aa
aaaa
,又
,,
∴ 为递减等差数列∴ 1110 SS 为最大。
4.已知等差数列 的前 10 项和为 100,前 100 项和
为 10,则前 110 项和为-110
解:∵
,,,,, 1001102030102010 SSSSSSS
成等差数列,公差为 D 其首项为
10010 S ,前 10 项的和为 10100 S
110221010100
10
22102
91010100
110
10100110
)(
又
,
S
DSSS
DD
10210
102)10(2
98402
42
)1(129850
max
2
2
yn
n
nn
nnnny
时,所以当
6.设等差数列 的前 n 项和为 nS ,已知
0012 13123 SSa ,,
①求出公差 d 的范围,
②指出 1221 SSS ,,, 中哪一个值最大,并说
明理由。
)(nfan na "2" n
解:① )(6)(6 10312112 aaaaS
37
24
30824
0)82(2
13
)(2
13
2
)(13
7
240724
0)72(6
3
113
131
13
3
d
dd
da
aaaaS
dd
da
从而
又
②
最大。, 667
713
7612
00
013
0)(6
Saa
aS
aaS
课外练习
一、 选择题
1. 已知 na 数列是等差数列, 1010 a ,其前 10
项的和 7010 S ,则其公差 等于( D )
3
2
3
1
3
1
3
2
..
..
DC
BA
2. 已知等差数列na 中,
12497 116 aaaa ,则, 等于( A )
A.15 B.30 C.31 D.64
1512
12497
a
aaaa解:
二、填空题
3. 设 为等差数列 的前 项和,
97104 3014 SSSS ,则, =54
4. 已 知 等 差 数 列 的前 项 和 为 ,若
1185212 21 aaaaS ,则
5. 设 F 是椭圆 167
22
yx 的右焦点,且椭圆上至
少有 21 个不同点
,
),2,1(
321 FPFPFP
iPi
,,
使
组 成 公 差 为 d 的 等 差 数 列 , 则 的 取 值 范 围 为
10
10010
1 ,,
解:椭圆的焦点 F 到椭圆上的点最大、最小距离分别
为 )和( 17)17( ,由题意得:
10
10010
1
010
1
2011
2
17)117
dd
dd
nnd
dn
或
,又
()(
三、解答题
6. 等 差 数 列 na 的前 n 项 和 记 为 nS , 已 知
5030 2010 aa ,
①求通项 na ;②若 =242,求
解: dnaan )1(1
1022
12
5019
309
5030
1
1
1
2010
nad
a
da
da
aa
n
解方程组
,
由
2
)1(
1
dnnnaSn
, =242
舍去)或解得 (2211
24222
)1(12
nn
nnn
7. 甲、乙两物体分别从相距 70 m 的两处同时相向运
动,甲第一分钟走 2 m ,以后每分钟比前一分钟多
走 1 ,乙每分钟走 5 ,①甲、乙开始运动后几
分钟相遇?②如果甲乙到对方起点后立即折返,甲
继续每分钟比前一分钟多走 1 ,乙继续每分钟走
5 ,那么,开始运动几分钟后第二次相遇?
解:①设 分钟后第一次相遇,依题意有:
舍去),解得 (207
7052
)1(2
nn
nnnn
故第一次相遇是在开始运动后 7 分钟。
②设 分钟后第二次相遇,则:
舍去),解得 (2815
70352
)1(2
nn
nnnn
故第二次相遇是在开始运动后 15 分钟
10 .已知数列 中, ,31a 前 和
1)1)(1(2
1 nn anS
①求证:数列 是等差数列
②求数列 的通项公式
③设数列
1
1
nnaa
的前 项和为 nT ,是否存在实
数 M ,使得 MTn 对一切正整数 都成立?若存
在,求 M 的最小值,若不存在,试说明理由。
解:①∵ 1)1)(1(2
1 nn anS
nnnn
nn
nn
nn
nnn
nn
anannaan
anan
anna
anan
SSa
anS
)1()2()1(
1)2()1(
1)1(
)1)(1()1)(2(2
1
1)1)(2(2
1
112
12
1
1
11
11
整理得,
nnn
nnn
aaa
aanan
21
21
2
))(1()1(2
∴数列 为等差数列。
② 1)1(3 11 nn annaa ,
12
2)1(3)1(
2
2
512
1
12
12
n
ndnaa
a
aa
aa
n
n 的公差为即等差数列
③
)32)(12(
11
1
nnaa nn
6
1
)32
1
3
1(2
1
)32
1
12
1
7
1
5
1
5
1
3
1(2
1
32
1
12
1
2
1
n
n
TNn
n
nnT
nn
时,又当
要使得 MTn 对一切正整数 n 恒成立,只要 M ≥
6
1 ,所以存在实数 使得 对一切正整数
都成立, 的最小值为
6
1 。
6.3 等比数列
知识要点
1. 定义:如果一个数列从第二项起,每一项与它的
前一项的比等于同一个常数,那么这个数列叫做等比
数列,这个常数叫做等比数列的公比,记为
)0qq,( 。
2. 递推关系与通项公式
mn
mn
n
n
nn
qaa
qaa
qaa
推广:
通项公式:
递推关系:
1
1
1
3. 等比中项:若三个数 cba ,, 成等比数列,则称 b 为
ca与 的等比中项,且为 acbacb 2,注:
是成等比数列的必要而不充分条件。
4. 前 项和公式
)1(
11
)1(
)1(
11
1
q
q
qaa
q
qa
qna
S n
n
n
5. 等比数列的基本性质, ),,,( Nqpnm其中
① qpnm aaaaqpnm ,则若 反之
不真!
② )(2
Nnaaaa
aq mnmnn
m
nmn ,
③ na 为等比数列,则下标成等差数列的对应项
成等比数列。
④ ,,,时, nnnnn SSSSSq 2321 仍
成等比数列。
6. 等比数列与等比数列的转化
① 是等差数列 )10( ccc na , 是
等比数列;
② 是 正 项 等 比 数 列
)10(log ccanc , 是等差数列;
③ 既是等差数列又是等比数列 是各
项不为零的常数列。
7. 等比数列的判定法
①定义法: (常数)qa
a
n
n 1 na 为等比数列;
②中项法: )0(2
2
1 nnnn aaaa 为
等比数列;
③通项公式法: 为常数)qkqka n
n ,(
为等比数列;④ 前 n 项和法:
为常数)( qkqkS n
n ,)1( 为 等 比 数
列。
1. 1031074 22222)( nnf 设
)18(7
2)18(7
2
)18(7
2)18(7
2
)()(
43
1
nn
nn
DC
BA
DnfNn
..
..
)(等于,则
2. 已知数列 是 等 比 数 列 , 且
mmm SSS 32 3010 ,则, 70 (问题引入)
猜想: nb 是等比数列,公比为
2
1 。
证明如下:∵
4
1
2
1
4
1
2121 nnn aab
nn
n
ba
a
2
1)4
1(2
1
4
1)4
1(2
1
12
12
即:
2
11
n
n
b
b ,∴ 是首项为
4
1a ,公比
为
2
1 的等比数列。
二、性质运用
例 2 : ⑴ 在 等 比 数 列 中,
14361 3233 nn aaaaaa ,,
①求 na ,
②若 nnn TaaaT 求,lglglg 21
⑵在等比数列 中,若 015 a ,则有等式
nn aaaaaa 292121
)29( Nnn , 成立,类比上述性质,相应的
在等比数列 中,若 119 b 则有等式 成
立。
解:⑴①由等比数列的性质可知:
nn
na
qqa
a
aa
aaaa
aaaa
61
5
1
6
61
6161
4361
2)2
1(32
2
1
32
1
32
1
132
33
32
所以
,,即所以
,解得
,又
②由等比数列的性质可知, nalg 是等差数
列,因为
2lg2
)11(
2
)lg(lg
2lg5lg2lg)6(2lglg
1
1
6
nnnaaT
ana
n
n
n
n
所以
,
⑵ 由题设可知,如果 0ma 在等差数列中有
nmn aaaaaa 122121
)12( Nnmn , 成 立 , 我 们 知 道 , 如 果
qpnm aaaaqpnm ,则若 ,而对于
等 比 数 列 ,则有
qpnm aaaaqpnm ,则若 所以可以得
出结论,若
nmnm bbbbbbb 1221211 ,则有
)12( Nnmn , 成立,在本题中
nn bbbbbb 372121 则有
)37( Nnn ,
点拨:历年高考对性质考查较多,主要是利用“等积
性”,题目“小而巧”且背景不断更新,要熟练掌握。
典例精析
一、 错位相减法求和
例 1:求和: nn a
n
aaaS 32
321
解:⑴
2
)1(3211 nnnSa n 时,
⑵ 01 aa 时,因为
①
132
1211
nnn a
n
a
n
aaSa ②
由①-②得:
)1)1(
)1()1(
)1(2
)1(
)1(
)1()1(
11
)11(1
111)11(
2
2
1
12
aaa
anaa
ann
S
aa
anaaS
a
n
a
aa
a
n
aaaSa
n
nn
n
n
n
n
n
nnn
综上所述,
所以
点拨:①若数列 na 是等差数列, nb 是等比数列,
则求数列 nn ba 的前 n 项和时,可采用错位
相减法;
②当等比数列公比为字母时,应对字母是否为
1 进行讨论;
③当将 nS 与 q 相减合并同类项时,注意错
位及未合并项的正负号。
二、 裂项相消法求和
例 2 :数列 满足 1a =8 ,
022 124 nnn aaaa ,且 ( Nn )
①求数列 的通项公式;
则 214
14
aad
所以, na =8+( -1)×(-2)=―10-2
②
32)2(4
1
)1(4
1
8
3
)2
1
1
1
2
11(4
1
)2
11()4
1
2
1()3
1
1
1(4
1
)2
11(4
1
)2(2
1
)14(
1
21
m
nn
nn
nn
bbbT
nn
nnanb
nn
n
n
所以
对一切 恒成立。
3
16
3
16
21
8
11
812
)2
8
1
812
2
8
1
812
min
m
nnNn
Nnnnm
所以
,(对
恒成立。对一切
故
m 的最大整数值为 5。
点拨:① 若 数 列 的 通 项 能 转 化 为
)()1( nfnf 的形式,常采用裂项相消法求和。
②使用裂项消法求和时,要注意正负项相消时,
消去了哪些项,保留了哪些项。
三、 奇偶分析法求和
例 3:设二次函数 1)( 2 nnxxxxf ,,当
1. 在等差数列 na 中, 1a =1,前 n 项和 nS 满足
,,, 211
242
nn
n
S
S
n
n
①求数列 的通项公式
②记 )0( ppab na
nn ,求数列 nb 的前
项和 nT 。
解:① 设数列 的公差为 d ,由
1
)1(2
2
)(
2
2)(
1
24
1
23
1
1
2
12
2
1
21
n
n
n
n
n
n
a
na
naa
nanda
S
S
n
n
aad
aa
aa
又
即
,所以得
所以 na =
②由 )0( ppab na
nn ,有 n
n npb
所以 n
n nppppT 32 32 ①
2
)1(1 nnTp n时,当
时,当 1p
132 )1(2 nn
n nppnpppT ②
①-②得
)1(1)1(
)1(
)1(2
)1(
1)1(
)1(
1
)1(
)1(
1
2
1
2
1
12
pp
np
p
pp
pnn
T
p
np
p
ppT
npp
pp
nppppTp
nnn
nn
n
n
n
nn
n
即:
所以
课外练习
1. 数列 的前 项 和 为 ,若
5)1(
1 Snnan ,则
等于( B )
6
5
)6
1
5
1()3
1
2
1()2
1
1
1(
1
11
)1(
1
30
1
6
1
6
51
5
S
nnnna
DCBA
n
所以
解:因为
....
4. )(xf 的定义域为 R ,且 )(xf 是以 2 为周期的
周期函数,数列 是首项为 )( Naa ,公差为
1 的等差数列,那么 )()()( 1021 afafaf 的
值为( C )
A.-1 B.1 C.0 D.10 a
解:因为函数 的定义域为 R ,且 是
以 2 为周期的周期函数,
所以 )()2(00( xfxff ,且)
又数列 是首项为 ,公差为 1 的等差数列
0)1()1()1(
)1()21()1(
)1(5)1()0(5
)1(5)(5
)()()(
)1(
)()(
1
1021
fff
fff
fff
afaf
afafaf
naf
nafaf
Nanaa
n
n
即所以
又
所以
为偶数)(
为奇数)(
,又所以
故原式=0,选 C。
二、填空题
5.设等比数列 na 的公比与前 n 项和分别为 q 和
nS ,且 ≠1, 818 10
20
10 q
SS ,则
8
1
)1(
8)1(1(
)1(
1
821
)1(
1010
20
10
1010
10
10
2012111020
10
20
1
10
20
10
1
S
q
S
qSSqS
aaaSS
qq
qa
q
S
qa
所以
方法二、
)
方法一、
6.数列 满足 12
1 2 1n
na n n n
,
1
2
n
nn
b aa
又 ,则数列 nb 的前 项和为
1
8
n
n
1 (1 2 )12n
nann
解:
1
28
( 1)n
nn
b a a n n
= 118( 1nn
)
12
1 1 1 1 1 18 ( ) ( ) ( )1 2 2 3 1
1881 11
nb b b
nn
n
nn
所以
7.数列 ,,,,,,,,,,
4
1
4
1
4
1
4
1
3
1
3
1
3
1
2
1
2
11 的前 100 项
的和为
14
913 。( Nn )
典例精析
一、 函数与数列的综合问题
的等差数列。,公差为是首项为
,,,设
,且:已知例
24
)()()()(
)10(log)(1
21
Nnafafaf
aaxxf
n
a
①设 a 是常数,求证: na 成等差数列;
②若 )( nnn afab , nb 的前 n 项和是 nS ,当 2a 时,求
解:① 222)1(4)( nnaf n ,
为等比数列。所以
为定值所以
,所以即
n
n
n
n
n
n
nna
a
na
a
a
a
a
aana
)2(
22log
2
2
22
1
22
② )( nnn afab
3
3
14
32543
3254
2543
222
222222
2
2)1(21
)21(216
2)1(22222
2)1(223222
2)1(242322
2)1()2()22(
2
)22(log
n
n
n
n
nn
n
nn
n
n
n
nn
n
nn
a
n
nS
n
nS
nnS
nS
nnb
a
anaa
所以
两式相减得
时,当
点 拨 : 本 例 是 数 列 与 函 数 综 合 的 基 本 题 型 之 一 , 特
征是以函数为载体构建数列的递推关系,通过由函数的解析式获知数列的通项公式,从而问题得到求解。
1. 已知正项数列 的前 项和为 , 2)1(4
1 nn aS 与是 的等比中项,
①求证:数列 是等差数列;
②若 n
n
n
ab
2
,数列 的前 项和为 nT ,求
③在②的条件下,是否存在常数 ,使得数列
2n
n
a
T 为等比数列?若存在,试求出 ;若不存在,说明理由。
解:① 2)1(4
1 nn aS 与是 的等比中项,
0)2)((
)22(4
1
)1(4
12
1)1(4
11
)1(4
1
11
1
2
1
2
1
2
11
1
2
11
2
nnnn
nnnn
nnn
nn
nn
aaaa
aaaa
SSa
aSn
aaan
aS
即
所以
时,当
,时,当
所以
2
020
1
1
nn
nnn
aa
aaa
即:
,所以因为
所以数列 na 是等差数列。
② nn
nT 2
323
32
1)2
323(
2
n
n
a
T
n
n
n
nn 2
1
32
3
所以当且仅当 3+ =0,即 =-3 时,数列
2n
n
a
T 为等比数列。
2. 已知在正项数列 中, 1a =2,且
), 1( nnn aaA 在双曲线 122 xy 上,
数列 nb 中,
点( nb , nT )在直线 12
1 xy 上,其中 是数列 的前 n 项和,①求数列 的通项公式;②求证:数列 是
等比数列。③若 nnnnn CCbaC 1,求证: 。
解:①由已知带点 ), 1( nnn aaA 在 上知,
1na - na =1,所以数列 是以 2 为首项,以 1 为公差的等差数列。
所以 1)1(1 ndnaan
②因为点( , )在直线 上,
11
11
1 121 12
11
22
nn
nn
n n n n n
Tb
Tb
b T T b b
所以
所以
两式相减得:
1
1 1 1
1
1
3 1211232
31
3 2 1 2()3 3 3
nn
n
n
n n
bb
n b b b
b
b
所以 ,
令 得 ,所以
所以 是一个以 为首项,
以 为公比的等比数列。
所以
③ nnnn nbaC 3
2)1(
nn
n
nnnn
CC
n
nnCC
1
1
11
0)12(3
2
3
2)1(
3
2)2(
所以
所以
一、选择题
1. ( 2009 广东卷理 ) 已 知 等 比 数 列 {}na 满足 0, 1,2,nan ,且
2
5 2 5 2 ( 3)n
na a n , 则 当 1n 时,
2 1 2 3 2 2 1log log logna a a
A. (2 1)nn B.
2( 1)n C. 2n D.
2( 1)n
【解析】由 得
n
na 22 2 , 0na ,则
n
na 2 , 3212 loglog aa
2
122 )12(31log nna n ,选 C.
答案 C
2.(2009 辽宁卷理)设等比数列{ na }的前 n 项和为 nS ,若
6
3
S
S =3 ,则 6
9S
S =
A. 2 B.
7
3 C.
8
3 D.3
【解析】设公比为 q ,则
3
63
33
(1 )S q S
SS
=1+q3=3 q3=2
于是 6
36
9
3
1 1 2 4 7
1 1 2 3
S qq
Sq
【答案】B
14.(2009 湖北卷理)已知数列 na 满足: 1
a =m (m 为正整数),
1
,2
3 1,
n
n
n
nn
a aa
aa
当 为偶数时,
当 为奇数时。若 6a =1,则 m 所有
可能的取值为__________。
答案 4 5 32
解析 (1)若 1am 为偶数,则
1
2
a
为偶, 故
2
23 a2 2 4
amma
①当 4
m
仍为偶数时, 468 32
mmaa
故
1 3232
m m
②当 为奇数时, 43
33 1 14a a m 6
3 14
4
m
a
故
3 14 14
m
得 m=4。
(2)若 为奇数,则 213 1 3 1a a m 为偶数,故 3
31
2
ma
必为偶数
6
31
16
ma
,所以
31
16
m
=1 可得 m=5
16.(2009 陕西卷文)设等差数列 na 的前 n 项和为 ns ,若 6312as,则 na .
解析:由 可得 的公差 d=2,首项 1a =2,故易得 2n.
答案:2n
17.(2009 陕西卷理)设等差数列 的前 n 项和为 nS ,若 6312aS,则 2lim n
n
S
n
.
6 1 1
22
31
12 5 12 2 11( 1) lim lim 112 12 2
nn
n nn
a ad a SSnnS n ns a d d n n n n
解析:
答案:1
22.(2009 全国卷Ⅰ理)在数列{}na 中, 11
111, (1 ) 2nnn
na a an
(I)设
n
n
ab n
,求数列{}nb 的通项公式
(II)求数列{}na 的前 n 项和 nS
分析:(I)由已知有
1 1
12
nn
n
aa
nn
1
1
2nnnbb
利用累差迭加即可求出数列 的通项公式: 1
12 2n nb
( *nN )
(II)由(I)知 12 2n n
nan
,
=
1
1
(2 )2
n
k
k
kk
1
11
(2 ) 2
nn
k
kk
kk
而 1
(2 ) ( 1)
n
k
k n n
,又
1
1 2
n
k
k
k
是一个典型的错位相减法模型,
易得
11
1
2422
n
kn
k
kn
= ( 1)nn 1
2 42n
n
23.(2009 北京理)已知数集 1 2 1 2, , 1 , 2nnA a a a a a a n 具有性质 P ;对任意的
,1i j i j n , ijaa 与
j
i
a
a 两数中至少有一个属于 A .
(Ⅰ)分别判断数集 1,3,4 与 1,2,3,6 是否具有性质 P ,并说明理由;
(Ⅱ)证明: 1 1a ,且
12
1 1 1
12
n
n
n
a a a aa a a
;
(Ⅲ)证明:当 5n 时, 1 2 3 4 5, , , ,a a a a a 成等比数列.
【解析】本题主要考查集合、等比数列的性质,考查运算能力、推理论证能力、分
分类讨论等数学思想方法.本题是数列与不等式的综合题,属于较难层次题.
(Ⅰ)由于34 与
4
3 均不属于数集 ,∴该数集不具有性质 P.
由于
6 6 1 2 3 61 2,1 3,1 6,2 3, , , , , ,2 3 1 2 3 6
都属于数集 ,
∴该数集具有性质 P.
(Ⅱ)∵ 12,, nA a a a 具有性质 P,∴ nnaa 与
n
n
a
a 中至少有一个属于 A,
由于 121 na a a ,∴ n n na a a ,故 nna a A .
从而
1 n
n
a Aa
,∴ 1 1a .
∵ 121 na a a , ∴ k n na a a ,故 2,3, ,kna a A k n .
由 A 具有性质 P 可知
1,2,3, ,n
k
a A k na
.
又∵ 1 2 1
n n n n
nn
a a a a
a a a a
,
∴
21
1 2 1
1, , ,n n n n
nn
nn
a a a aa a aa a a a
,
从而
1 2 1
1 2 1
n n n n
nn
nn
a a a a a a a aa a a a
,
∴
12
1 1 1
12
n
n
n
a a a aa a a
.
(Ⅲ)由(Ⅱ)知,当 5n 时,有
55
23
43
,aaaaaa
,即
2
5 2 4 3a a a a,
∵ 1 2 51 a a a ,∴ 3 4 2 4 5a a a a a,∴ 34a a A ,
由 A 具有性质 P 可知
4
3
a Aa
.
2
2 4 3a a a ,得
3 4
23
a a Aaa
,且
3
2
2
1 a aa
,∴
34
2
32
aa aaa
,
∴
5342
2
4 3 2 1
aaaaaa a a a
,即 1 2 3 4 5, , , ,a a a a a 是首项为 1,公比为 2a 成等比数列.
25(2009 江苏卷)对于正整数 n ≥2,用 nT 表示关于 x 的一元二次方程 2 20x ax b 有实数根的有序数组( , )ab 的
组数,其中 , 1,2, ,a b n ( a 和b 可以相等);对于随机选取的 ( 和 可以相等),记 nP 为关于
的一元二次方程 有实数根的概率。
(1)求 2nT 和 2nP ;
(2)求证:对任意正整数 n ≥2,有
11nP
n
.
【解析】 [必做题]本小题主要考查概率的基本知识和记数原理,考查探究能力。满分 10 分。
29.(2009 江西卷理)各项均为正数的数列{}na , 12,a a a b,且对满足 m n p q 的正整数 , , ,m n p q都有
.(1 )(1 ) (1 )(1 )
pqmn
m n p q
aaaa
a a a a
(1)当
14,25ab
时,求通项 ;na
(2)证明:对任意 a ,存在与 a 有关的常数 ,使得对于每个正整数 n ,都有
1 .na
解:(1)由 (1 )(1 ) (1 )(1 )
pqmn
m n p q
aaaa
a a a a
得
1 2 1
1 2 1
.(1 )(1 ) (1 )(1 )
nn
nn
a a a a
a a a a
将 12
14,25aa
代入化简得
1
1
21.2
n
n
n
aa a
所以
1
1
111 ,1 3 1
nn
nn
aa
aa
故数列
1{}1
n
n
a
a
为等比数列,从而
1 1 ,13
n
n
n
a
a
即
31.31
n
n na
可验证,
31
31
n
n na 满足题设条件.
(2) 由题设 (1 )(1 )
mn
mn
aa
aa
的值仅与 mn 有关,记为 ,mnb 则
1
1
1
.(1 )(1 ) (1 )(1 )
nn
n
nn
a a a ab a a a a
考察函数
( ) ( 0)(1 )(1 )
axf x xax
,则在定义域上有
1 ,11
1( ) ( ) , 12
, 0 11
aa
f x g a a
a aa
故对 *nN , 1 ()nb g a 恒成立.
又
2 2
2 ()(1 )
n
n
n
ab g aa ,
注意到
10 ( ) 2ga
,解上式得
1 ( ) 1 2 ( ) 1 ( ) 1 2 ( )() ,( ) ( )1 ( ) 1 2 ( ) n
g a g a g a g aga ag a g ag a g a
取
1 ( ) 1 2 ( )
()
g a g a
ga
,即有
1 .na
.
30. (2009 湖北卷理)已知数列 na 的前 n 项和
11( ) 22
n
nnSa
(n 为正整数)。
(Ⅰ)令 2n
nnba ,求证数列 nb 是等差数列,并求数列 的通项公式;
(Ⅱ)令
1
nn
ncan
, 12........nnT c c c 试比较 nT 与
5
21
n
n 的大小,并予以证明。
解(I)在
11( ) 22
n
nnSa
中,令 n=1,可得 1112nS a a ,即 1
1
2a
当 2n 时,
21
1 1 1 1
11( ) 2 ( )22
nn
n n n n n n nS a a S S a a
,
,
11
n 1 1
12a ( ) , 2 12
nn
n n na a a
n即2
.
112 , 1, n 2 1n
n n n n nb a b b b n即当 时,b .
又 112 1,ba 数列 nb 是首项和公差均为 1 的等差数列.
于是
1 ( 1) 1 2 , 2
n
n n n n
nb n n a a
.
(II)由(I)得
11( 1)( )2
n
nn
nc a nn
,所以
231 1 1 12 3 ( ) 4 ( ) ( 1)( )2 2 2 2
n
nTn K
2 3 4 11 1 1 1 12 ( ) 3 ( ) 4 ( ) ( 1)( )2 2 2 2 2
n
nTn K
由①-②得
2 3 11 1 1 1 11 ( ) ( ) ( ) ( 1)( )2 2 2 2 2
nn
nTn K
1
1
1
11[1 ( ) ] 1 3 3421 ( 1)( )1 2 2 21 2
33 2
n
n
n
n n
nn
nT
5 3 5 ( 3)(2 2 1)32 1 2 2 1 2 (2 1)
n
n nn
n n n n nT n n n
于是确定
5
21n
nT n
与
的大小关系等价于比较 2 2 1n n与 的大小
由
2 3 4 52 2 1 1;2 2 2 1;2 2 3 1;2 2 4 1;2 2 5; K
可猜想当 3 2 2 1.nnn 时, 证明如下:
证法 1:( 1)当 n=3 时,由上验算显示成立。
(2)假设 1nk时
12 2 2 2(2 1) 4 2 2( 1) 1 (2 1) 2( 1) 1kkk k k k k g
所以当 时猜想也成立
综合(1)( 2)可知 ,对一切 3n 的正整数,都有 2 2 1.n n
证法 2:当 3n 时
0 1 2 1 0 1 12 (1 1) 2 2 2 1n n n n n n
n n n n n n n n nC C C C C C C C C n n K
综上所述,当 1,2n 时
5
21n
nT n ,当 时
5
21n
nT n
31.(2009 四川卷文)设数列 na 的前 n 项和为 nS ,对任意的正整数 n ,都有 51nnaS成立,记
*4 ()1
n
n
n
ab n Na
。
(I)求数列 na 与数列 nb 的通项公式;
(II)设数列 的前 项和为 nR ,是否存在正整数 k ,使得 4nRk 成立?若存在,找出一个正整数 ;若不存在,
请说明理由;
(III)记
*
2 2 1()n n nc b b n N ,设数列 nc 的前 项和为 nT ,求证:对任意正整数 n 都有
3
2nT
;
解(I)当 1n 时, 1 1 1
15 1, 4 a S a
又 115 1, 5 1 n n n na S a S
1
11
15, 4
即
n
n n n
n
aa a a a
∴数列 是首项为 1
1
4a
,公比为
1
4q
的等比数列,
∴
1()4 n
na
,
*
14 ( )4 ()11 ( )4
n
n
n
b n N
…………………………………3 分
(II)不存在正整数 ,使得 成立。
证明:由(I)知
14 ( ) 54 41 ( 4) 11 ( )4
n
n n
n
b
2 1 2 2 1 2
5 5 5 20 15 16 408 8 8 8.( 4) 1 ( 4) 1 16 1 16 4 (16 1)(16 4)
k
kk k k k k k kbb
∴当 n 为偶数时,设 2 ( )n m m N
∴ 1 2 3 4 2 1 2( ) ( ) ( ) 8 4n m mR b b b b b b m n
当 n 为奇数时,设 2 1( )n m m N
∴ 1 2 3 4 2 3 2 2 2 1( ) ( ) ( ) 8( 1) 4 8 4 4n m m mR b b b b b b b m m n
∴对于一切的正整数 n,都有 4nRk
∴不存在正整数 k ,使得 4nRk 成立。 …………………………………8 分
(III)由
54 ( 4) 1n nb 得
2 1 2 2 2 1 2 2
5 5 15 16 15 16 15 16 15
4 1 4 1 (16 1)(16 4) (16 ) 3 16 4 (16 ) 16
n n n
n n n n n n n n n n nc b b
又
1 2 2
13 43, ,33b b c
,
当 1n 时, 1
3
2T
,
当 2n 时,
2
2
23
2
11[1 ( ) ]4 1 1 1 4 16 1625 ( ) 25 13 16 16 16 3 1 16
1
4 69 31625 13 48 21 16
n
n nT
32.(2009 湖南卷文)对于数列{}nu ,若存在常数 M>0,对任意的 *nN ,恒有
1 1 2 1n n n nu u u u u u M , 则称数列 为 B 数列.
(Ⅰ)首项为 1,公比为
1
2
的等比数列是否为 B-数列?请说明理由;
(Ⅱ)设 nS 是数列{}nx 的前 n 项和.给出下列两组判断:
A 组:①数列 是 B-数列, ②数列 不是 B-数列;
B 组:③数列{}nS 是 B-数列, ④数列 不是 B-数列.
请以其中一组中的一个论断为条件,另一组中的一个论断为结论组成一个命题.
判断所给命题的真假,并证明你的结论;
(Ⅲ)若数列{}na 是 B-数列,证明:数列
2{}na 也是 B-数列。
解: (Ⅰ)设满足题设的等比数列为 ,则
11()2
n
na
.于是
1 2 2
1
1 1 3 1( ) ( ) ( ) , 2.2 2 2 2
n n n
nna a n
1 1 2 1| | | | | |n n n na a a a a a
=
2n3 1 1 112 2 2 2
-1( ) ( )
=
n13 1 3.2
( )
所以首项为 1,公比为
1
2
的等比数列是 B-数列 .
(Ⅱ)命题 1:若数列{}nx 是 B-数列,则数列{}nS 是 B-数列.此命题为假命题.
事实上设 nx =1, *nN ,易知数列 是 B-数列,但 nS =n,
1 1 2 1| | | | | |n n n nS S S S S S n .
由 n 的任意性知,数列 不是 B-数列。
命题 2:若数列 是 B-数列,则数列 不是 B-数列。此命题为真命题。
事实上,因为数列 是 B-数列,所以存在正数 M,对任意的 ,有
1 1 2 1| | | | | |n n n nS S S S S S M ,
即 12| | | | | |nnx x x M .于是 1 1 2 1n n n nx x x x x x
1 1 2 1 12 2 2 2n n nx x x x x M x ,
所以数列 是 B-数列。
(注:按题中要求组成其它命题解答时,仿上述解法)
(Ⅲ)若数列 na 是 B-数列,则存在正数 M,对任意的 ,nN 有
1 1 2 1n n n na a a a a a M .
因为 1 1 2 2 1 1n n n n na a a a a a a a
1 1 2 2 1 1 1n n n na a a a a a a M a .
记 1K M a,则有
22
1 1 1( )( )n n n n n na a a a a a
1 1 1( ) 2n n n n n na a a a K a a .
因此
2 2 2 2 2 2
1 1 2 1... 2n n n na a a a a a KM .
故数列 2
na 是 B-数列.
33. (2009 陕西卷理) 已知数列 }nx 满足,
*
11
11,21n
n
x x n Nx +
’
= =
.
猜想数列{}nx 的单调性,并证明你的结论;
(Ⅱ)证明:
1
1
12| ( )65
n
nnxx
-|≤
。
证明(1)由
1 n+1 2 4 4
n
1 1 2 5 13
2 1 3 8 21x x x x xx
及 得 ,
由 2 4 6xxx猜想:数列 2nx 是递减数列
下面用数学归纳法证明:
(1)当 n=1 时,已证命题成立 (2)假设当 n=k 时命题成立,即 2 2 2kkxx
易知 2 0kx ,那么
2 3 2 1
2 2 2 4
2 1 2 3 2 1 2 3
11
1 1 (1 )(1 )
kk
kk
k k k k
xxxx x x x x
=
2 2 2
2 2 1 2 2 2 3
0(1 )(1 )(1 )(1 )
kk
k k k k
xx
x x x x
即 2( 1) 2( 1) 2kkxx
也就是说,当 n=k+1 时命题也成立,结合(1)和(2)知,命题成立
(2)当 n=1 时, 1 2 1
1
6nnx x x x
,结论成立
当 2n 时,易知
11
1
110 1, 1 2, 12n n n
n
x x x x
1 1 1
1
15(1 )(1 ) (1 )(1 ) 212n n n n
n
x x x xx
1
1
11
11
1 1 (1 )(1 )
nn
nn
n n n n
xxxx x x x x
2 n-1
1 1 2 2 1
n-1
2 2 2
5 5 5
12
65
n n n nx x x x x x
( ) ( )
( )
35.(2009 天津卷理)已知等差数列{
na
}的公差为 d(d 0),等比数列{ nb }的公比为 q(q>1)。设 ns = 11ab+ 22ab…..+
nnab
, nT = 11ab- 22ab+…..+(-1
1)n
nnab
,n N
若 1a = 1b = 1,d=2,q=3,求 3S 的值;
若 1b =1,证明(1-q) 2nS -(1+q) 2nT =
2
2
2 (1 )
1
ndq q
q
,n N ;
(Ⅲ) 若正数n满足2 n q,设 1 2 1 2, ,..., , ,..., 1 2 ...nnk k k l l l和 是 ,,,n 的两个不同的排列, 121 1 2 ... nk k k nc a b a b a b ,
122 1 2 ... nl l l nc a b a b a b 证明
12cc
。
本小题主要考查等差数列的通项公式、等比数列的通项公式与前 n 项和公式等基础知识,考查运算能力,推理论证能
力及综合分析和解决问题的能力的能力,满分 14 分。
(Ⅰ)解:由题设,可得
1*2 1, 3 ,n
nna n b n N
所以, 3 1 1 2 2 3 3 1 1 3 3 5 9 55S a b a b a b
(Ⅱ)证明:由题设可得
1n
nbq 则
2 2 1
2 1 2 3 2..... ,n
nnS a a q a q a q ①
2 3 2 1
2 1 2 3 4 2
3 2 1
2 2 2 4 2
..... ,
2( ... )
n
nn
n
n n n
T a a q a q a q a q
S T a q a q a q
②
式减去②式,得
式加上②式,得
2 2 2
2 2 1 3 2 12( .... )n
n n nS T a a q a q
③
式两边同乘 q,得
3 2 1
2 2 1 3 2 1( ) 2( .... )n
n n nq S T a q a q a q
所以,
2 2 2 2 2 2(1 ) (1 ) ( ) ( )n n n n n nq S q T S T q S T
3 2 1
2
*
2
2 ( )
2 (1 ) ,1
n
n
d q q q
dq q nNq
K
(Ⅲ)证明: 1 1 2 21 2 1 2( ) ( ) ( )nnk l k l k l nc c a a b a a b a a b K
1
1 1 1 2 2 1 1( ) ( ) ( ) n
nnk l db k l db q k l db q K
因为 10, 0,db所以
112
1 1 2 2
1
( ) ( ) ( ) n
nn
cc k l k l q k l qdb
K
若 nnkl ,取 i=n
若 nnkl ,取 i 满足 iikl 且 ,1jjk l i j n
由(1),(2)及题设知,1 in 且
2112
1 1 2 2 1 1
1
( ) ( ) ( ) ( )ii
i i i i
cc k l k l q k l q k l qdb
K
当 iikl 时,得 1, 1, 1,2,3..... 1i i i ik l q n k l q i i 由 ,得
即 11 1k l q , 22( ) ( 1)k l q q q …,
22
11( ) ( 1)ii
iik l q q q
又
11( ) ,ii
iik l q q 所以
1
2112
1
1( 1) ( 1) ( 1) ( 1) 1
i
iicc qq q q q q q qdb q
K
因此 1 2 1 20,c c c c 即
当 iikl 同理可得
12
1
1cc
db
,因此 12cc
综上,
37.(2009 年上海卷理)已知 na 是公差为 d 的等差数列, nb 是公比为 q 的等比数列。
若 31nan,是否存在 *m k N、 ,有 1 ?m m ka a a说明理由;
找出所有数列 和 ,使对一切 *nN ,
1n
n
n
a ba
,并说明理由;
若 115, 4, 3,a d b q 试确定所有的 p ,使数列 na 中存在某个连续 项的和是数列 nb 中的一项,请证明。
[解法一](1)由 1m m ka a a,得6 5 3 1mk , ......2 分
整理后,可得
42 3km
, m 、 k N , 2km 为整数,
不存在 、 ,使等式成立。 ......5 分
(2)若
1n
n
a ba
,即
11
1
1 ( 1)
na nd bqa n d
, (*)
(ⅰ)若 0,d 则
1
11 n
nb q b。
当{ na }为非零常数列,{ nb }为恒等于 1 的常数列,满足要求。 ......7 分
(ⅱ)若 0d ,( *)式等号左边取极限得
1
1
lim 1( 1)n
a nd
a n d
,( *)式等号右边的极限只有当 1q 时,才能等于 1。
此时等号左边是常数, 0d,矛盾。
综上所述,只有当{ }为非零常数列,{ }为恒等于 1 的常数列,满足要求。......10 分
【解法二】设
1,,n
n n n
n
aa nd c b ba
若 且 为等比数列
则
*221
21
1
/,nn
n n n
nn
aa q n N a a qaaa
对 都成立,即
2( )( 2 ) ( )dn c dn d c q dn d c * 2 2....7n N a qd 对 都成立, 分
若 d=0,则
*0, 1,nna c b n N
若 0,d 则q=1, nbm(常数)即
dn d c mdn c
,则 d=0,矛盾
综上所述,有
n
n
n
nn ba
aNbca 1*,n,1,0 使对一切
, 10 分
(3) *,3,14 Nnbna n
nn
设 NmNkpbaa k
kpmmm ,,3a *
21 、 .
kppmm 32
1)(41)1(4
,
NspNpppm
k
,3*,k,3324 5、
. 13 分
取 ,03)14(2)14(33234,23 2222 ssssmsk 15 分
由二项展开式可得正整数 M1、M2,使得(4-1)2s+2=4M1+1,
,2)1(8)14(2 2
ss M
.,21)1()2(44 21 满足要求存在整数mMMm s
故当且仅当 p=3s,sN 时,命题成立.
说明:第(3)题若学生从以下角度解题,可分别得部分分(即分步得分)
若 p 为偶数,则 am+1+am+2+……+am+p 为偶数,但 3k 为奇数
故此等式不成立,所以,p 一定为奇数。
当 p=1 时,则 am+1=bk,即 4m+5=3k,
而 3k=(4-1)k
= ,,)1(4)1()1(4)1(44 11110 ZMMCCCC kkk
k
kk
k
k
k
k
k
当k为偶数时,存在m,使4m+5=3k 成立 1 分
当 p=3 时,则 am+1+am+2+am+3=bk,即 3am+2-bk,
也即 3(4m+9)=3k,所以 4m+9=3k-1,4(m+1)+5=3k-1
由已证可知,当 k-1 为偶数即 k 为奇数时,存在 m, 4m+9=3k 成立 2 分
当 p=5 时,则 am+1+am+2+……+am+5=bk,即 5am+3=bk
也即 5(4m+13)=3k,而 3k 不是 5 的倍数,所以,当 p=5 时,所要求的 m 不存在
故不是所有奇数都成立. 2 分
三、解答题
10.(2008 全国 I)设函数 ( ) lnf x x x x .数列 na 满足 101a, 1 ()nna f a .
(Ⅰ)证明:函数 ()fx在区间(01), 是增函数;
(Ⅱ)证明: 1 1nnaa;
(Ⅲ)设 1( 1)ba , ,整数
1
1 ln
abk ab
≥
.证明: 1kab .
(Ⅰ)证明: , ' ln , 0,1 ' ln 0f x x x f x x 当 时,
故函数 fx在区间(0,1)上是增函数;
(Ⅱ)证明:(用数学归纳法)(i)当 n=1 时, , 11ln 0aa ,
2 1 1 1 1 1( ) lna f a a a a a
由函数 在区间 是增函数,且函数 在 1x 处连续,则 在区间(01],是增函数,
2 1 1 1 1( ) ln 1a f a a a a ,即 121aa成立;
(ⅱ)假设当 ( *)x k k N 时, 1 1kkaa成立,即 1101kka a a ≤
那么当 1nk时,由 ()fx在区间(01],是增函数, 得
1( ) ( ) (1)kkf a f a f.而 1 ()nna f a ,则 1 2 1( ), ( )k k k ka f a a f a ,
121kkaa,也就是说当 时, 1 1nnaa也成立;
根据(ⅰ)、(ⅱ)可得对任意的正整数 n , 恒成立.
(Ⅲ)证明:由 ( ) lnf x x x x . 1 ()nna f a 可
kkkk aababa ln1
1
1
ln
k
ii
i
a b a a
若存在某ik≤ 满足 iab≤ ,则由⑵知: 1kia b a b ≥0
若对任意 都有 bai ,则
1
1
ln
k
i
i
a b a b
1
1
( )ln
k
i
i
a b a b
bkaba ln11
bkaba ln11 )(11 baba 0 ,即 1kab 成立.
11.(2008 山东卷)将数列{an}中的所有项按每一行比上一行多一项的规则排成如下数表:
a1
a2 a3
a4 a5 a6
a7 a8 a9 a10
……
记表中的第一列数 a1,a2,a4,a7,…构成的数列为{bn},b1=a1=1. Sn 为数列{bn}的前 n 项和,且满足= nNn
n
SSb
b
2
2
1=
(n≥2).
(Ⅰ)证明数列{ nS
1
}成等差数列,并求数列{bn}的通项公式;
(Ⅱ)上表中,若从第三行起,每一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当 91
4
81 a
时,
求上表中第 k(k≥3)行所有项和的和.
12.(2007 湖南)已知 ()n n nA a b, ( nN*)是曲线
xye 上的点, 1aa , nS 是数列{}na 的前 n 项和,且满足
2 2 2
13n n nS n a S , 0na , 234n ,,,….
(I)证明:数列
2n
n
b
b
( 2n≤ )是常数数列;
(II)确定 a 的取值集合 M ,使 aM 时,数列{}na 是单调递增数列;
(III)证明:当 aM 时,弦 1nnAA ( nN*)的斜率随 n 单调递增
解:(I)当 2n≥ 时,由已知得
2 2 2
1 3n n nS S n a .
因为 1 0n n na S S ,所以
2
1 3nnS S n. …… ①
于是
2
1 3( 1)nnS S n . ……②
由②-①得 1 63nna a n . …… ③
于是 2169nna a n . …… ④
由④-③得 2 6nnaa , …… ⑤
所以
2
2 62
n
nn
n
a
aan
a
n
b e eebe
,即数列
2 ( 2)n
n
b nb
≥
是常数数列.
(II)由①有 2112SS,所以 2 12 2aa.由③有 3215aa, 4321aa,所以 3 32aa , 4 18 2aa.
而 ⑤表明:数列 2{}ka 和 21{}ka 分别是以 2a , 3a 为首项,6 为公差的等差数列,
所以 226( 1)ka a k , 2 1 3 6( 1)ka a k , 2 2 4 6( 1)( )ka a k k N* ,
数列{}na 是单调递增数列 12aa且 2 2 1 2 2k k ka a a对任意的 k N*成立.
且 2346( 1) 6( 1) 6( 1)a k a k a k
1 2 3 4a a a a
9 1512 2 3 2 18 2 44a a a a a
.
即所求 a 的取值集合是
9 15
44M a a
.
(III)解法一:弦 1nnAA 的斜率为
1
1
11
nnaa
nn
n
n n n n
bbeek a a a a
任取 0x ,设函数
0
0
()
xxeefx xx
,则
0
0
2
0
( ) ( )() ()
xxxe x x e efx xx
记
0
0( ) ( ) ( )xxxg x e x x e e ,则 00( ) ( ) ( )x x x xg x e x x e e e x x ,
当 0xx 时, ( ) 0gx , ()gx在 0()x , 上为增函数,
当 0xx 时, ( ) 0gx , ()gx在 0()x, 上为减函数,
所以 0xx 时, 0( ) ( ) 0g x g x,从而 `( ) 0fx ,所以 ()fx在 0()x, 和 0()x , 上都是增函数.
由(II)知, aM 时,数列{}na 单调递增,
取 0 nxa ,因为 12n n na a a,所以
1
1
nnaa
n
nn
eek aa
2
2
nnaa
nn
ee
aa
.
取 02nxa ,因为 ,所以
12
1
12
nnaa
n
nn
eek aa
2
2
nnaa
nn
ee
aa
.
所以 1nnkk ,即弦 1()nnA A n N* 的斜率随 n 单调递增.
解法二:设函数
1
1
()
nax
n
eefx xa
,同解法一得, ()fx在 1()na , 和 1()na , 上都是增函数,
所以
11
1
111
lim
n n n
n
n
a a ax
a
n nan n n
e e e ekea a x a
→ ,
2 1 1
1
1
1
2 1 1
lim
n n n
n
n
a a ax
a
n nan n n
e e e ekea a x a
→ .
故 ,即弦 的斜率随 单调递增.
5.(辽宁省沈阳二中 2008—2009 学年上学期高三期中考试)
数列
,,141,1}{ 22
2
2
1211 nn
n
nn aaaS
a
aaa 记满足
若 3012
mSS nn
对任意 *Nn 恒成立,则正整数
m 的最小值 ( )
A.10 B.9 C.8 D.7
答案:A.