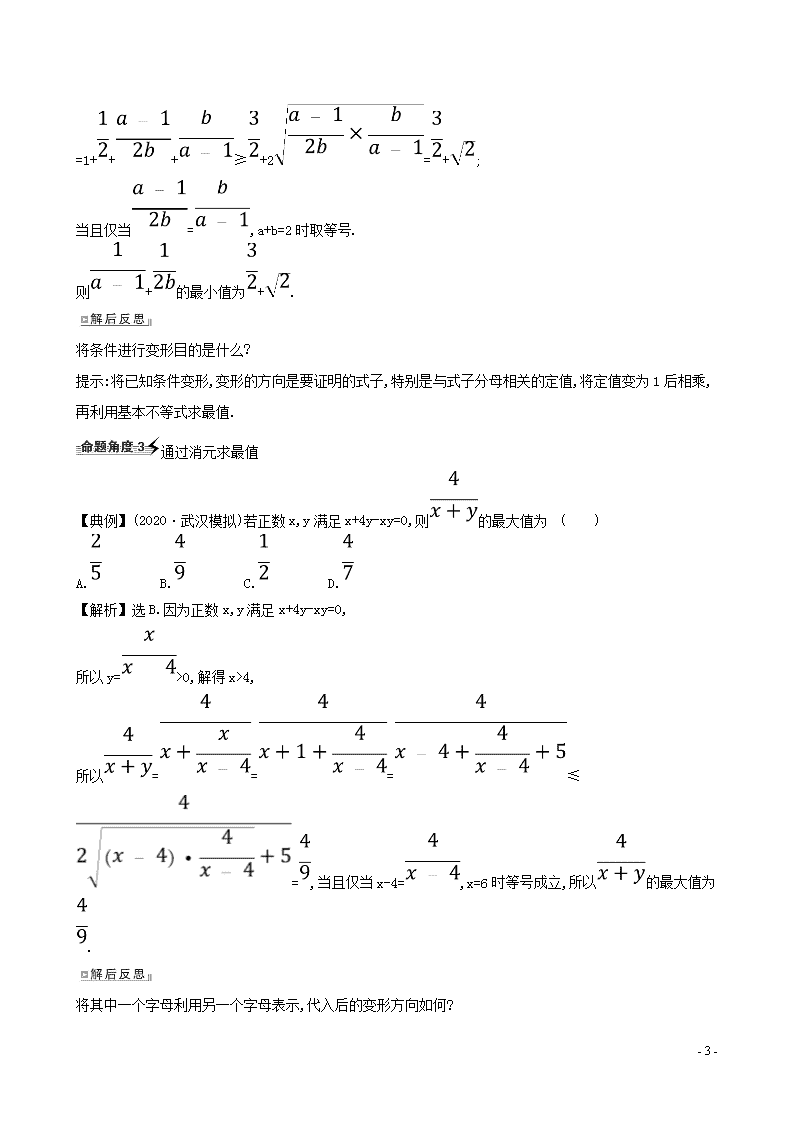高考数学一轮复习第六章不等式6-2基本不等式练习理北师大版 10页

‎6.2 基本不等式 核心考点·精准研析 考点一　利用基本不等式求最值 ‎ 命 题 精 解 读 ‎1.考什么:(1)考查求最值,证明不等式等问题.‎ ‎(2)考查数学运算、数学抽象、逻辑推理的核心素养.‎ ‎2.怎么考:求式子的最值,证明不等式、与函数结合考查求函数的值域,与解析几何结合求面积等几何量的最值.‎ ‎3.新趋势:与函数相结合求值域.‎ 学 霸 好 方 法 ‎1.求最值的解题思路 ‎(1)拼凑法:拼凑成积或和为定值,利用基本不等式求相应的最值.‎ ‎(2)构造法:通过对已知条件的变形,构造定值,代入后利用基本不等式求值.‎ ‎(3)消元法:当要求最值的式子中含有多个字母时,应考虑利用已知条件减少字母的个数,以达到利用基本不等式求最值的目的.‎ ‎2.交汇问题: ‎ 与方程、不等式交汇时,涉及恒成立问题、参数的范围等.‎ 通过拼凑定值求最值 ‎【典例】1.已知a,b>0,则+的最小值为　　　. ‎ ‎【解析】因为a,b>0,方法一:原式=+1+-1=+-1≥2-1=‎ ‎4-1=3,‎ 当且仅当=,a=b时取等号.‎ 方法二:所以+=+1+-1≥2-1=3,‎ - 10 -‎ 当且仅当+1=,即a=b时取等号.‎ 答案:3‎ ‎2.若x<,则f(x)=4x-2+的最大值为　　　. ‎ ‎【解析】因为x<,所以5-4x>0,‎ 则f(x)=4x-2+=-+3≤-2+3=-2+3=1.‎ 当且仅当5-4x=,即x=1时,等号成立.‎ 故f(x)=4x-2+的最大值为1.‎ 答案:1‎ 本例不能直接运用基本不等式时怎么办?‎ 提示:通过分子分母同除以a统一式子的结构或直接加1变形,再观察拼凑定值利用基本不等式求最小值.‎ 通过常值代换求最值 ‎【典例】(2019·深圳模拟)已知a>1,b>0,a+b=2,则+的最小值为 (　　)‎ A.+ B.+ C.3+2 D.+‎ ‎【解析】选A.已知a>1,b>0,a+b=2,‎ 可得(a-1)+b=1,a-1>0,‎ 则+=[(a-1)+b]‎ - 10 -‎ ‎=1+++≥+2=+;‎ 当且仅当=,a+b=2时取等号.‎ 则+的最小值为+.‎ 将条件进行变形目的是什么?‎ 提示:将已知条件变形,变形的方向是要证明的式子,特别是与式子分母相关的定值,将定值变为1后相乘,再利用基本不等式求最值.‎ 通过消元求最值 ‎【典例】(2020·武汉模拟)若正数x,y满足x+4y-xy=0,则的最大值为 (　　)‎ A.　 B.　 C.　 D.‎ ‎【解析】选B.因为正数x,y满足x+4y-xy=0,‎ 所以y=>0,解得x>4,‎ 所以===≤=,当且仅当x-4=,x=6时等号成立,所以的最大值为.‎ 将其中一个字母利用另一个字母表示,代入后的变形方向如何?‎ - 10 -‎ 提示:构造定值以利用基本不等式求最值.‎ 构造二次不等式求最值 ‎【典例】(2019·重庆模拟)已知a,b,c均为正实数,且ab+2a+b=6,则2a+b的最小值为　　　.  ‎ ‎【解析】因为a,b,c均为正实数,且ab+2a+b=6,‎ 所以6-2a-b=ab=×2ab≤,‎ 所以(2a+b)2+8(2a+b)-48≥0,所以2a+b≥4,‎ 当且仅当a=1,b=2时取等号,所以2a+b的最小值为4.‎ 答案:4‎ 本题利用基本不等式,将已知式子进行转换的目标是什么?‎ 提示:转化成关于2a+b的二次不等式,通过解不等式求最值.‎ ‎1.设x,y∈R,且xy≠0,则的最小值为 (　　)‎ A.-9　 B.9　　 C.10 D.0‎ ‎2.(2020·厦门模拟)已知00,b>0,且2a+b=ab-1,则a+2b的最小值为(　　)‎ A.5+2 B.8 C.5 D.9‎ ‎4.已知正数x,y满足x2+2xy-3=0,则2x+y的最小值是 (　　)‎ A.1　 B.3　 C.6　　 D.12‎ ‎【解析】1.选B.=5++x2y2≥5+2=9,‎ - 10 -‎ 当且仅当xy=±时,上式取得等号,可得最小值为9.‎ ‎2.选D.因为00,‎ 所以+=(x+1-x)‎ ‎=5++≥5+2=9,‎ 当且仅当=,即x=时取等号,‎ 所以+取得最小值时x=.‎ ‎3.选A.因为a>0,b>0,且2a+b=ab-1,‎ 所以a=>0,所以b>2,‎ 所以a+2b=+2b=2(b-2)++5‎ ‎≥5+2=5+2,‎ 当且仅当2(b-2)=,即b=2+时取等号.‎ 所以a+2b的最小值为5+2.‎ ‎4.选B.因为x2+2xy-3=0,所以y=,‎ 所以2x+y=2x+==+‎ ‎≥2=3.当且仅当=,即x=1时取等号.‎ - 10 -‎ ‎(2020·马鞍山模拟)已知△ABC的内角A,B,C的对边分别为a,b,c,若-ccos B是acos B与bcos A的等差中项,则sin 2A·tan 2C的最大值为　　　. ‎ ‎【解析】因为-ccos B是acos B与bcos A的等差中项,所以-2ccos B=‎ acos B+bcos A,‎ 所以-2sin Ccos B=(sin Acos B+cos Asin B)=sin(A+B)=sin C,所以cos B=-,因为角B为三角形内角,所以B=,所以A+C=,所以C=-A,所以 sin 2A·tan 2C=sin 2A ‎=sin 2A=sin 2A,令sin 2A=x,因为0