- 125.50 KB
- 2021-06-10 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
课时达标检测(二十五)两角差的余弦公式
一、选择题
1.cos 165°的值是( )
A. 6- 2
2
B. 6+ 2
2
C. 6- 2
4
D.
- 6- 2
4
答案:D
2.满足 cos αcos β= 3
2
-sin αsin β的一组α,β的值是( )
A.α=13π
12
,β=3π
4 B.α=π
2
,β=π
3
C.α=π
2
,β=π
6 D.α=π
3
,β=π
4
答案:B
3.已知 cos θ+π
6 = 5
13
,0<θ<π
3
,则 cos θ等于( )
A.5 3+12
26
B.12-5 3
13
C.5+12 3
26
D.6+5 3
13
答案:A
4.已知 cos x-π
6 =m,则 cos x+cos x-π
3 =( )
A.2m B.±2m
C. 3m D.± 3m
答案:C
5.已知△ABC 的三个内角分别为 A,B,C,若 a=(cos A,sin A),b=(cos B,sin B),
且 a·b=1,则△ABC 一定是( )
A.直角三角形 B.等腰三角形
C.等边三角形 D.等腰直角三角形
答案:B
二、填空题
6.计算: 2
2 (cos 75°+sin 75°)=________.
答案: 3
2
7.已知 sin α+sin β+sin γ=0 和 cos α+cos β+cos γ=0,则 cos(α-β)的值是________.
答案:-1
2
8.已知 cos(α+β)=4
5
,cos(α-β)=-4
5
,3π
2 <α+β<2π,π
2<α-β<π,则 cos 2β=________.
答案:-1
三、解答题
9.已知向量 a=(cos α,sin α),b=(cos β,sin β),|a-b|=2 5
5
,求 cos(α-β)的值.
解:∵a=(cos α,sin α),b=(cos β,sin β),
∴a-b=(cos α-cos β,sin α-sin β).
∴|a-b|= cos α-cos β2+sin α-sin β2
= cos2α-2cos αcos β+cos2β+sin2α-2sin αsin β+sin2β
= 2-2cosα-β=2 5
5
,
∴2-2cos(α-β)=4
5
,
∴cos(α-β)=3
5.
10.已知 sin α=12
13
,cos β=-3
5
,α、β均为第二象限角,求 cos(α-β)的值.
解:由 sin α=12
13
,α为第二象限角,
∴cos α=- 1-sin2α=- 1-
12
13 2=- 5
13.
又由 cos β=-3
5
,β为第二象限角,
∴sin β= 1-cos2β= 1- -3
5 2=4
5.
∴cos(α-β)=cos αcos β+sin αsin β
= - 5
13 × -3
5 +12
13
×4
5
=63
65.
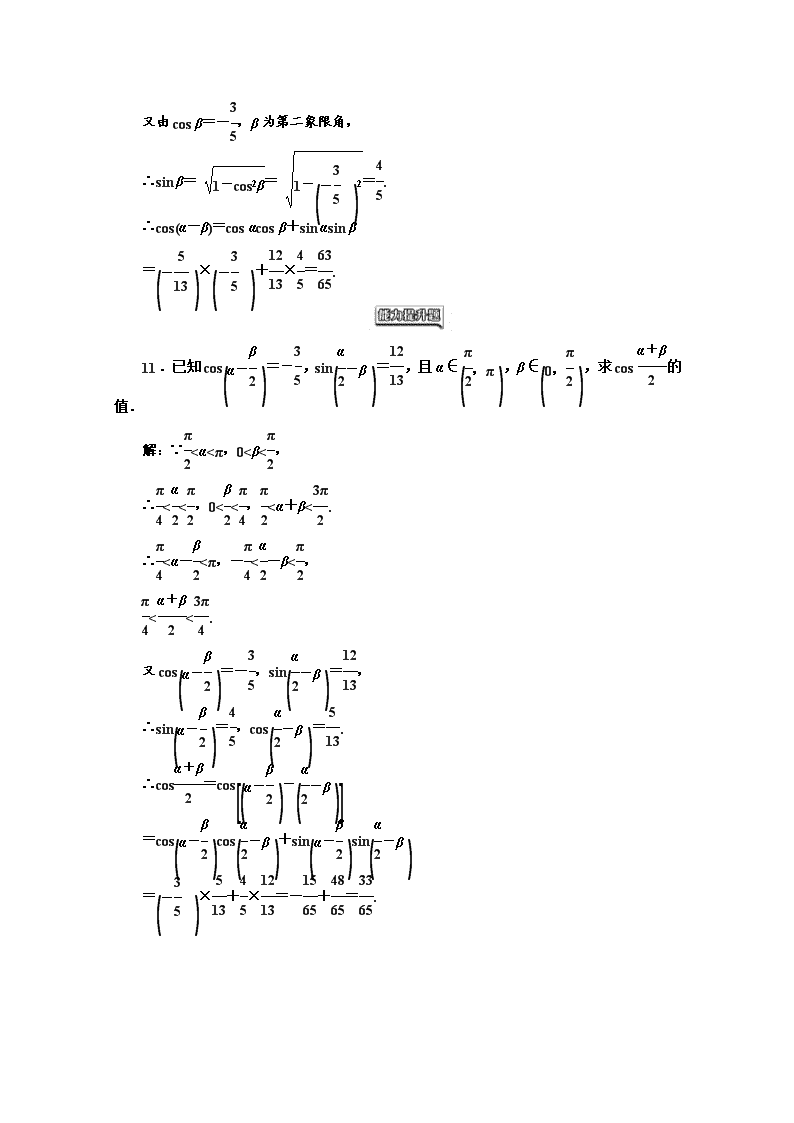
11.已知 cos α-β
2 =-3
5
,sin
α
2
-β =12
13
,且α∈
π
2
,π ,β∈ 0,π
2 ,求 cos α+β
2
的值.
解:∵π
2<α<π,0<β<π
2
,
∴π
4<α
2<π
2
,0<β
2<π
4
,π
2<α+β<3π
2 .
∴π
4<α-β
2<π,-π
4<α
2
-β<π
2
,
π
4<α+β
2
<3π
4 .
又 cos α-β
2 =-3
5
,sin
α
2
-β =12
13
,
∴sin α-β
2 =4
5
,cos
α
2
-β = 5
13.
∴cosα+β
2
=cos α-β
2 -
α
2
-β
=cos α-β
2 cos
α
2
-β +sin α-β
2 sin
α
2
-β
= -3
5 × 5
13
+4
5
×12
13
=-15
65
+48
65
=33
65.
相关文档
- 2017-2018学年广西桂林中学高二上2021-06-1012页
- 2017 年芜湖市高中毕业班教学质量2021-06-109页
- 江苏省连云港市2019-2020高二数学2021-06-1011页
- 人教版高三数学总复习课时作业202021-06-109页
- 2018-2019学年内蒙古巴彦淖尔一中2021-06-108页
- 新课标高一数学同步测试2(必修2-142021-06-106页
- 数学文卷·2019届广东省揭阳市惠来2021-06-108页
- 2018-2019学年山西省长治二中高二2021-06-107页
- 高二数学下学期期中试题理实验班2021-06-1017页
- 2019学年高二数学下学期期中试题 2021-06-109页