高中数学北师大版新教材必修一同步课件：5-1-1　利用函数性质判定方程解的存在性 39页

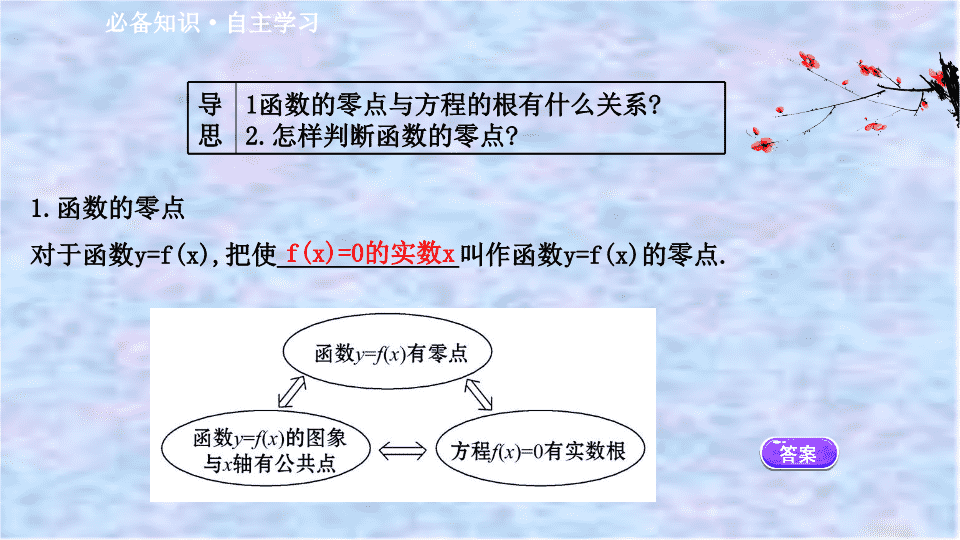
第五章　函 数 应 用 §1 　方程解的存在性及方程的近似解 1.1 　利用函数性质判定方程解的存在性 必备知识 · 自主学习 1. 函数的零点 对于函数 y=f(x), 把使 ______________ 叫作函数 y=f(x) 的零点 . 导思 1 函数的零点与方程的根有什么关系 ? 2. 怎样判断函数的零点 ? f(x)=0 的实数 x 【 思考 】 函数的“零点”是一个点吗 ? 请说明理由 . 提示 : 不是 , 函数的“零点”是一个数 , 一个使 f(x)=0 的实数 x; 实际上是函数 y=f(x) 的图象与 x 轴交点的横坐标 . 2. 零点存在定理 (1) 零点存在定理 : 若函数 y=f(x) 在闭区间 [a,b] 上的图象是一条 _____ 的曲线 , 并且在区间端点的函数值 _________, 即 _____________, 则在开区间 (a,b) 内 , 函 数 y=f(x) 至少有一个零点 , 即在区间 (a,b) 内相应的方程 _______ 至少有一个解 . (2) 本质 : 函数在区间 (a,b) 内存在零点即方程 f(x)=0 有解的理论依据 . (3) 应用 : 判断函数零点 ( 方程的解 ) 所在区间或求规定区间内函数零点 ( 方程的 解 ) 的个数等问题 . 连续 一正一负 f(a)·f(b)<0 f(x)=0 【 思考 】 函数零点存在定理要求具备哪些条件 ? 提示 : 定理要求具备两个条件 :① 函数在区间 [a,b] 上的图象是连续不断的一条曲线 ;②f(a)·f(b)<0. 【 基础小测 】 1. 辨析记忆 ( 对的打“√” , 错的打“ ×”). (1) 任何函数都有零点 . ( 　　 ) (2) 若 f(a)·f(b) >0, 则 f(x) 在 [a,b] 内无零点 . ( 　　 ) (3) 若函数 y=f(x) 在区间 (a,b) 上有零点 , 则一定有 f(a)·f(b)<0. ( 　　 ) 提示 : (1) ×, 有些函数如 f(x)=3 x 不存在零点 . (2)×. 当函数满足 f(a) · f(b)>0 时 , 函数 f(x) 在 [a,b] 内可能有两个零点 . (3)×. 例如 , 函数 f(x)=x 2 存在零点 x=0, 但不满足 f(a) · f(b)<0. 2. 函数 y=2x-1 的零点是 ( 　　 ) 【 解析 】 选 A. 由 2x-1=0 得 x= . 3.( 教材二次开发 : 例题改编 ) 下列各图象表示的函数中没有零点的是 ( 　　 ) 【 解析 】 选 D. 结合函数零点的定义可知选项 D 没有零点 . 关键能力 · 合作学习 类型一　函数零点的概念及求法 ( 数学抽象 ) 【 题组训练 】 1. 下列函数不存在零点的是 ( 　　 ) 2. 判断下列函数是否存在零点 , 如果存在 , 请求出 . (1)f(x)= ; (2)f(x)=x 2 +2x+4; (3)f(x)=2 x -3; (4)f(x)=1-log 3 x. 【 解析 】 1. 选 D. 由 x- =0, 得 x=±1, 故选项 A 不适合 ; 由 2x 2 -x-1=0 得 x=1 或 x= - , 故选项 B 不适合 ; 由 得 x=-1, 由 得 x=1, 故选项 C 不适合 ; 选项 D 中函数无零点 . 2.(1) 令 =0, 解得 x=-3, 所以函数 f(x)= 的零点是 -3. (2) 令 x 2 +2x+4=0, 由于 Δ=2 2 -4×4=-12<0, 所以方程 x 2 +2x+4=0 无解 , 所以函数 f(x)=x 2 +2x+4 不存在零点 . (3) 令 2 x -3=0, 所以 2 x =3, 解得 x=log 2 3, 所以函数 f(x)=2 x -3 的零点是 log 2 3. (4) 令 1-log 3 x=0, 所以 log 3 x=1, 解得 x=3, 所以函数 f(x)=1-log 3 x 的零点是 3. 【 解题策略 】 求函数 y=f(x) 的零点的两种方法 (1) 令 f(x)=0, 根据解方程 f(x)=0 的根求得函数的零点 ; (2) 画出函数 y=f(x) 的图象 , 图象与 x 轴的交点的横坐标即为函数的零点 . 【 补偿训练 】 函数 f(x)= 的所有零点构成的集合为 ( 　　 ) 　　　　　　　　　　　　　　　　　　 A.{1} B.{-1} C.{-1,1} D.{-1,0,1} 【 解析 】 选 C. 当 x≤0 时 ,f(x)=x+1=0 ⇒ x=-1; 当 x>0 时 ,f(x)= lo g 2 x=0 ⇒ x=1, 所以函数 f(x) 的所有零点构成的集合为 {-1,1}. 类型二　判断函数零点所在的区间 ( 数学运算、直观想象 ) 【 典例 】 函数 f(x)=ln x- 的零点所在的大致区间是 ( 　　 ) 　　　　　　　　　　　　　　　　　　 A.(1,2) B.(2,3) C.(3,4) D.(e,+∞) 【 思路导引 】 根据零点存在定理 , 寻找满足 f(a)·f(b)<0 的区间 (a,b). 【 解析 】 选 B. 函数 f(x)=ln x- 在 (0,+∞) 上单调递增 , 又因为 f(1)=-2<0,f(2)=ln 2-1<0, 所以在 (1,2) 内 f(x) 无零点 ,A 错 ; 又 f(3)=ln 3- >0, 所以 f(2) · f(3)<0, 所以 f(x) 在 (2,3) 内有零点 . 【 解题策略 】 判断函数零点所在区间的步骤 (1) 代入 : 将区间端点值代入函数求出函数的值 . (2) 判断 : 把所得的函数值相乘 , 并进行符号判断 . (3) 结论 : 若符号为正且函数在该区间内是单调函数 , 则在该区间内无零点 , 若符号为负且函数连续 , 则在该区间内至少有一个零点 . 【 跟踪训练 】 根据表格中的数据 , 可以断定方程 e x -(x+2)=0(e≈2.72) 的一个根所在的区间 是 ( 　　 ) A.(-1,0) B.(0,1) C.(1,2) D.(2,3) x -1 0 1 2 3 e x 0.37 1 2.72 7.40 20.12 x+2 1 2 3 4 5 【 解析 】 选 C. 令 f(x)=e x -(x+2), 则 f(-1)=0.37-1<0,f(0)=1-2<0, f(1)=2.72-3<0,f(2)=7.40-4=3.40>0. 由于 f(1) · f(2)<0, 所以方程 e x -(x+2)=0 的一个根在 (1,2) 内 . 类型三　函数零点个数问题 ( 逻辑推理、直观想象 ) 　角度 1 　图象法求函数零点的个数  【 典例 】 判断函数 f(x)=ln x+x 2 -3 的零点的个数为 ( 　　 ) 　　　　　　　　　　　　　　　　　　 A.1 B.2 C.3 D.4 【 思路导引 】 将原函数转化为两个函数 y=ln x 与 y=3-x 2 , 在同一平面直角坐标系中作出两个函数的图象 , 根据函数图象交点的个数得出原函数零点的个数 . 【 解析 】 选 A. 函数对应的方程为 ln x+x 2 -3=0, 所以原函数零点的个数即为函数 y=ln x 与 y=3-x 2 的图象交点个数 . 在同一平面直角坐标系下 , 作出两函数的图象 ( 如图 ). 由图象知 , 函数 y=3-x 2 与 y=ln x 的图象只有一个交点 . 从而 ln x+x 2 -3=0 有一个根 , 即函数 f(x)=ln x+x 2 -3 有一个零点 . 【 变式探究 】 将典例中函数改为 y=a |x| -|log a x|(00 时 , 由 -2+ln x=0 得 x=e 2 . 所以函数的零点个数为 2. 　角度 3 　利用函数零点求参数的值  【 典例 】 已知 a 是实数 , 函数 f(x)=2|x-1|+x-a, 若函数 y=f(x) 有且仅有两个零点 , 则实数 a 的取值范围是 　　　　 .  【 思路导引 】 转化为 y=2|x-1|+x 与 y=a 两个函数图象有且仅有两个交点的问题 . 【 解析 】 函数 f(x)=2|x-1|+x-a 有且仅有两个零点 , 即函数 y=2|x-1|+x 与 y=a 有且仅有两个交点 . 分别作出函数 y=2|x-1|+x 与 y=a 的图象 , 如图所示 . 由图易知 , 当 a>1 时 , 两函数的图象有两个不同的交点 , 故实数 a 的取值范围是 (1,+∞). 答案 : (1,+∞) 【 解题策略 】 1. 图象法求函数零点的个数 由 f(x)=g(x)-h(x)=0, 得 g(x)=h(x), 在同一平面直角坐标系内作出 y 1 =g(x) 和 y 2 =h(x) 的图象 , 根据两个图象交点的个数来判定函数零点的个数 . 2. 根据函数零点个数求参数值 ( 范围 ) 的方法 (1) 直接法 : 直接根据题设条件构建关于参数的不等式 , 通过解不等式确定参数的取值范围 . (2) 分离参数法 : 先将参数分离 , 然后转化成求函数值域问题加以解决 . (3) 数形结合法 : 先对解析式变形 , 在同一平面直角坐标系中 , 画出函数的图象 , 然后数形结合求解 . 【 题组训练 】 1. 函数 f(x)=x- 的零点的个数是 ( 　　 ) A.0 B.1 C.2 D.3 【 解析 】 选 C. 令 f(x)=0, 即 x- =0, 所以 x=±2, 故有两个 . 2. 若 f(x)=2 x ·(x-a)-1 在 (0,+∞) 内有零点 , 则 a 的取值范围是 ( 　　 ) A.(-∞,+∞) B.(-2,+∞) C.(0,+∞) D.(-1,+∞) 【 解析 】 选 D. 由题意可得 a=x- (x>0). 令 g(x)=x- , 该函数在 (0,+∞) 上单调递增 , 可知 g(x) 的值域为 (-1,+∞), 故 a>-1 时 ,f(x) 在 (0,+∞) 内有零点 . 3. 若函数 f(x)=x+ (a∈R) 在区间 (1,2) 上有零点 , 则 a 的值可能是 ( 　　 ) 　　　　　　　　　　　　　　　　　　 A.-2 B.0 C.1 D.3 【 解析 】 选 A.f(x)=x+ (a∈R) 的图象在 (1,2) 上是连续不断的 , 逐个选项代入 验证 , 当 a=-2 时 ,f(1)=1-2=-1<0,f(2)=2-1=1>0. 故 f(x) 在区间 (1,2) 上有零点 ; 同理 , 其他选项不符合 . 课堂检测 · 素养达标 1. 函数 f(x)=2x 2 -3x+1 的零点是 ( 　　 ) A.- ,-1 　 B. ,1 C. ,-1 D.- ,1 【 解析 】 选 B. 方程 2x 2 -3x+1=0 的两根分别为 x 1 =1,x 2 = , 所以函数 f(x)=2x 2 - 3x+1 的零点是 ,1. 2. 函数 f(x)=2 x - 的零点所在的区间是 ( 　　 ) 【 解析 】 选 B. 由 f(x)=2 x - 得 f( )= -2<0, f(1)=2-1=1>0, 所以 f( ) · f (1)<0. 因为函数 f(x)=2 x - 的图象是一条连续的曲线 , 所以由函数零点存在定理可知零点所在区间为 . 3.( 教材二次开发 : 练习改编 ) 下列图象表示的函数中没有零点的是 ( 　　 ) 【 解析 】 选 A. 因为 B,C,D 的图象均与 x 轴有交点 , 故函数均有零点 ,A 的图象与 x 轴没有交点 , 故函数没有零点 . 4. 函数 f(x)=2 x +x-2 有 　　　　 个零点 .  【 解析 】 在同一平面直角坐标系中作出函数 y=2 x , y=-x+2 的图象 , 由图可知函数 f(x) 有 1 个零点 . 答案 : 1 5. 已知函数 f(x)=x 2 -x-2a. (1) 若 a=1, 求函数 f(x) 的零点 ; (2) 若 f(x) 有零点 , 求实数 a 的取值范围 . 【 解析 】 (1) 当 a=1 时 ,f(x)=x 2 -x-2. 令 x 2 -x-2=0, 得 x=-1 或 x=2. 即函数 f(x) 的零点为 -1 和 2. (2) 要使 f(x) 有零点 , 则方程 x 2 -x-2a=0 有解 , 即 Δ=1+8a≥0, 解得 a≥- , 所以 a 的取值范围是 a≥- .