2021高三数学人教B版一轮学案：第二章 第十一节　第1课时　导数与函数的单调性 15页

www.ks5u.com 第十一节　导数的简单应用 最新考纲 考情分析 ‎1.了解函数的单调性与导数的关系；能利用导数研究函数的单调性，会求函数的单调区间(其中多项式函数不超过三次)．‎ ‎2．了解函数在某点取得极值的必要条件和充分条件；会用导数求函数的极大值、极小值(其中多项式函数不超过三次)；会求闭区间上函数的最大值、最小值(其中多项式函数不超过三次).‎ ‎1.利用导数求函数的单调区间及极值(最值)、结合单调性与不等式的成立情况求参数范围是高考命题的热点．‎ ‎2．常与基本初等函数的图象与性质、解析几何、不等式、方程等交汇命题，主要考查转化与化归思想、分类讨论思想的应用．‎ ‎3．题型主要以解答题为主，属中高档题.‎ ‎　　　　　　　　　　　　　　　　 ‎ 知识点一　　函数的单调性与导数的关系 函数y＝f(x)在某个区间内可导，则：‎ ‎(1)若f′(x)>0，则f(x)在这个区间内单调递增；‎ ‎(2)若f′(x)<0，则f(x)在这个区间内单调递减；‎ ‎(3)若f′(x)＝0，则f(x)在这个区间内是常数函数．‎ 函数f(x)在区间(a，b)上递增，则f′(x)≥0，“f′(x)>0在(a，b)上成立”是“f(x)在(a，b)上单调递增”的充分不必要条件．‎ 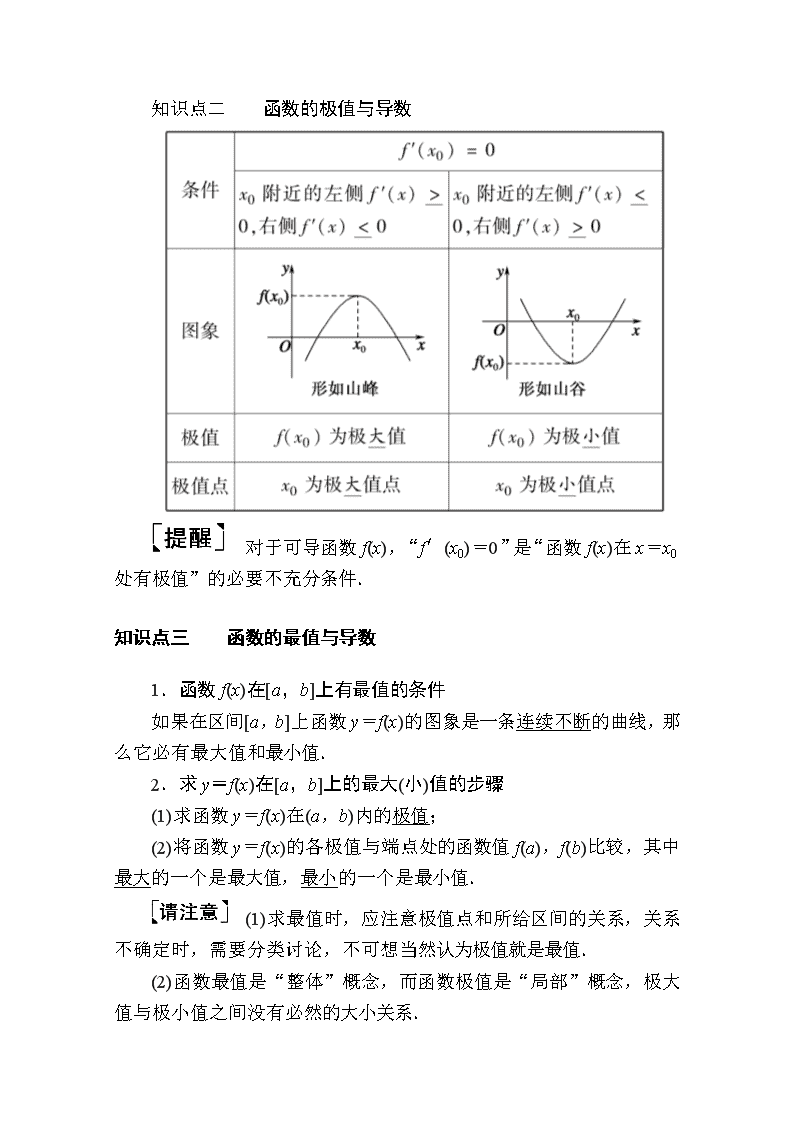知识点二　　函数的极值与导数 对于可导函数f(x)，“f′(x0)＝‎0”‎是“函数f(x)在x＝x0处有极值”的必要不充分条件．‎ 知识点三　　函数的最值与导数 ‎1．函数f(x)在[a，b]上有最值的条件 如果在区间[a，b]上函数y＝f(x)的图象是一条连续不断的曲线，那么它必有最大值和最小值．‎ ‎2．求y＝f(x)在[a，b]上的最大(小)值的步骤 ‎(1)求函数y＝f(x)在(a，b)内的极值；‎ ‎(2)将函数y＝f(x)的各极值与端点处的函数值f(a)，f(b)比较，其中最大的一个是最大值，最小的一个是最小值．‎ ‎(1)求最值时，应注意极值点和所给区间的关系，关系不确定时，需要分类讨论，不可想当然认为极值就是最值．‎ ‎(2)函数最值是“整体”概念，而函数极值是“局部”概念，极大值与极小值之间没有必然的大小关系．‎ ‎1．思考辨析 判断下列结论正误(在括号内打“√”或“×”)‎ ‎(1)若函数f(x)在(a，b)内单调递增，那么一定有f′(x)>0.(　×　)‎ ‎(2)如果函数f(x)在某个区间内恒有f′(x)＝0，则f(x)在此区间内没有单调性．(　√　)‎ ‎(3)函数的极大值一定大于其极小值．(　×　)‎ ‎(4)对可导函数f(x)，f′(x0)＝0是x0为极值点的充要条件．(　×　)‎ ‎(5)函数的最大值不一定是极大值，函数的最小值也不一定是极小值．(　√　)‎ 解析：(1)f(x)在(a，b)内单调递增，则有f′(x)≥0.‎ ‎(3)函数的极大值也可能小于极小值．‎ ‎(4)x0为f(x)的极值点的充要条件是f′(x0)＝0，且x0两侧导函数异号．‎ ‎2．小题热身 ‎(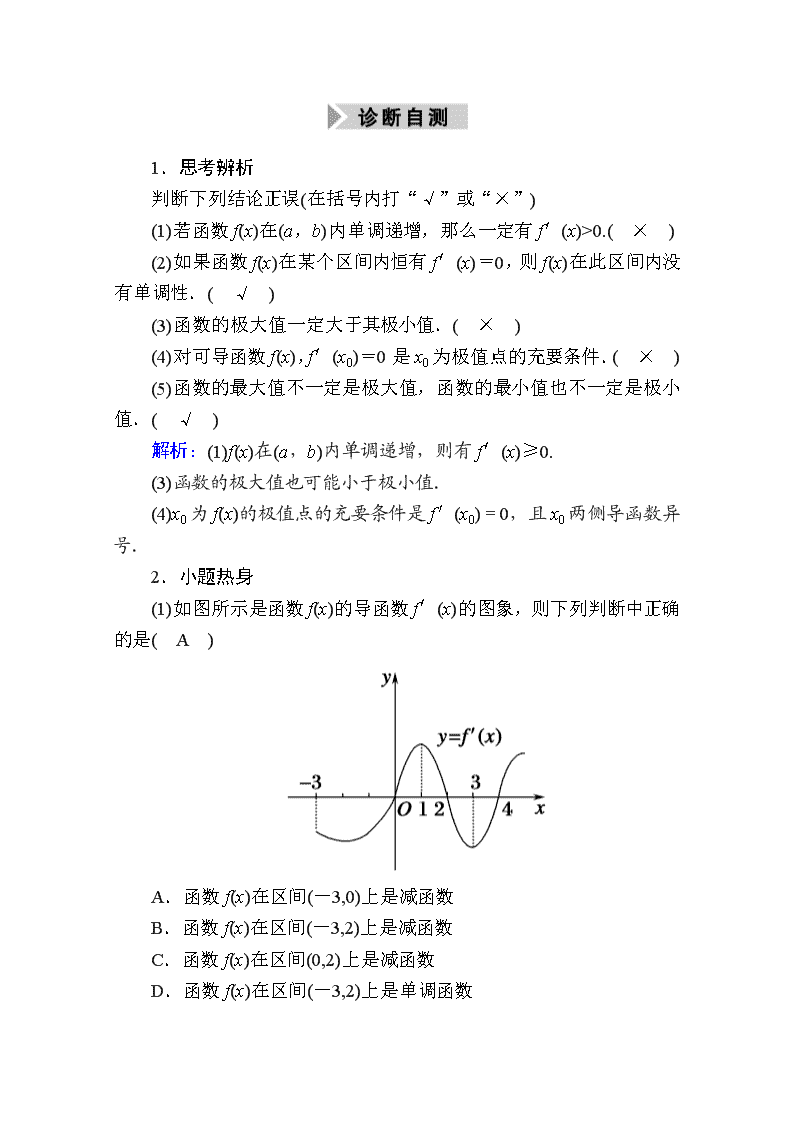1)如图所示是函数f(x)的导函数f′(x)的图象，则下列判断中正确的是(　A　)‎ A．函数f(x)在区间(－3,0)上是减函数 B．函数f(x)在区间(－3,2)上是减函数 C．函数f(x)在区间(0,2)上是减函数 D．函数f(x)在区间(－3,2)上是单调函数 解析：当x∈(－3,0)时，f′(x)<0，则f(x)在(－3,0)上是减函数．其他判断均不正确．‎ ‎(2)如图是f(x)的导函数f′(x)的图象，则f(x)的极小值点的个数为(　A　)‎ A．1 B．2‎ C．3 D．4‎ 解析：由题意知在x＝－1处f′(－1)＝0，且其左右两侧导数符号为左负右正．‎ ‎(3)函数f(x)＝(x－3)ex的单调递增区间是(　D　)‎ A．(－∞，2) B．(0,3)‎ C．(1,4) D．(2，＋∞)‎ 解析：函数f(x)＝(x－3)ex的导数为f′(x)＝[(x－3)ex]′＝ex＋(x－3)ex＝(x－2)ex.由函数导数与函数单调性的关系，得当f′(x)>0时，函数f(x)单调递增，此时由不等式f′(x)＝(x－2)ex>0，解得x>2.‎ ‎(4)函数f(x)＝x3－4x＋4在[0,3]上的最大值与最小值分别为4，－.‎ 解析：由f(x)＝x3－4x＋4，得f′(x)＝x2－4＝(x－2)(x＋2)，令f′(x)>0，得x>2或x<－2；‎ 令f′(x)<0，得－20，得单调递增区间；④在定义域内解不等式f′(x)<0，得单调递减区间.,(2)若所求函数的单调区间不止一个时，用“，”或“和”连接.‎ ‎1．已知函数f(x)＝xlnx，则f(x)(　D　)‎ A．在(0，＋∞)上递增 B．在(0，＋∞)上递减 C．在上递增 D．在上递减 解析：因为函数f(x)＝xlnx，定义域为(0，＋∞)，所以f′(x)＝lnx＋1(x>0)，当f′(x)>0时，解得x>，即函数的单调递增区间为；当f′(x)<0时，解得00，则其在区间(－π，π)上的解集为和，即f(x)的单调递增区间为，.‎ 考点二　讨论函数的单调性 ‎【例2】　已知函数f(x)＝x－＋1－alnx，讨论f(x)的单调性．‎ ‎【解】　函数f(x)的定义域为(0，＋∞)，导函数f′(x)＝1＋－＝，x∈(0，＋∞)．‎ 设g(x)＝x2－ax＋2，二次方程g(x)＝0的判别式Δ＝a2－8.‎ ‎(1)当Δ≤0，即－2≤a≤2时，‎ 对∀x>0，都有f′(x)≥0，‎ ‎∴f(x)在(0，＋∞)上单调递增．‎ ‎(2)当Δ>0，即a<－2或a>2时，‎ 若a>2，方程g(x)＝0有两个不相等的正实数根 x1＝，x2＝，02时，f(x)在，上单调递增；在上单调递减．‎ 方法技巧 讨论含参函数的单调性是高考的常驻考点，定义域范围内的导函数的零点是否为变号零点是决定函数单调性改变的充要条件，可以画导函数图象的草图帮助判定正负情况.‎ 已知函数f(x)＝lnx－ax2＋(1－a)x＋1，a∈R，讨论f(x)的单调性．‎ 解：函数f(x)的定义域为(0，＋∞)．‎ f′(x)＝－ax＋(1－a)＝.‎ 当a≤0时，f′(x)>0在(0，＋∞)上恒成立，‎ ‎∴f(x)在(0，＋∞)上单调递增．‎ 当a>0时，‎ f′(x)＝＝.‎ 方程f′(x)＝0有两个不相等的实数根x1＝，x2＝－1，x2<00时，f(x)在上单调递增，在上单调递减．‎ 考点三　函数单调性的简单应用 命题方向1　　比较大小或解不等式 ‎【例3】　(1)已知函数y＝f(x)对于任意的x∈ 满足f′(x)cosx＋f(x)sinx＝1＋lnx，其中f′(x)是函数f(x)的导函数，则下列不等式成立的是(　　)‎ A.ff C.f>f D.f>f ‎(2)已知函数f′(x)是函数f(x)的导函数，f(1)＝，对任意实数都有f(x)－f′(x)>0，设F(x)＝，则不等式F(x)<的解集为(　　)‎ A．(－∞，1) B．(1，＋∞)‎ C．(1，e) D．(e，＋∞)‎ ‎【解析】　(1)令g(x)＝，‎ 则g′(x)＝＝.‎ 由解得，所以g>g，所以>，即f>f.‎ ‎(2)F′(x)＝＝，‎ 又f(x)－f′(x)>0，知F′(x)<0，‎ ‎∴F(x)在R上单调递减．‎ 由F(x)<＝F(1)，得x>1，‎ 所以不等式F(x)<的解集为(1，＋∞)．‎ ‎【答案】　(1)B　(2)B 命题方向2　　根据单调性求参数取值范围 ‎【例4】　(2020·昆明诊断)已知函数f(x)＝lnx，g(x)＝ax2＋2x.‎ ‎(1)若函数h(x)＝f(x)－g(x)存在单调递减区间，求实数a的取值范围；‎ ‎(2)若函数h(x)＝f(x)－g(x)在[1,4]上单调递减，求实数a的取值范围．‎ ‎【解】　h(x)＝lnx－ax2－2x，x>0.‎ ‎∴h′(x)＝－ax－2.‎ ‎(1)若函数h(x)在(0，＋∞)上存在单调减区间，则当x>0时，－ax－2<0有解，即a>－有解．‎ 设G(x)＝－，所以只要a>G(x)min.‎ 又G(x)＝2－1，所以G(x)min＝－1.‎ 所以a>－1.即实数a的取值范围是(－1，＋∞)．‎ ‎(2)∵h(x)在[1,4]上单调递减，‎ ‎∴当x∈[1,4]时，h′(x)＝－ax－2≤0恒成立，‎ 则a≥－恒成立，‎ 设G(x)＝－，所以a≥G(x)max.‎ 又G(x)＝2－1，x∈[1,4]，‎ 因为x∈[1,4]，所以∈，‎ 所以G(x)max＝－(此时x＝4)，‎ 所以a≥－.‎ 又当a＝－时，h′(x)＝＋x－2＝，‎ ‎∵x∈[1,4]，∴h′(x)＝≤0，当且仅当x＝4时等号成立．‎ ‎∴h(x)在[1,4]上为减函数．‎ 故实数a的取值范围是.‎ 方法技巧 (1)利用导数比较大小或解不等式，其关键在于利用题目条件构造辅助函数，把比较大小的问题转化为先利用导数研究函数的单调性，进而根据单调性比较大小或解不等式.‎ (2)根据函数单调性求参数的一般思路 ‎①利用集合间的包含关系处理：y＝f(x)在(a，b)上单调，则区间(a，b)是相应单调区间的子集.‎ ‎②f(x)是单调递增的充要条件是对任意的x∈(a，b)都有f′(x)≥0且在(a，b)内的任一非空子区间上，f′(x)不恒为零，应注意此时式子中的等号不能省略，否则漏解.‎ ‎③函数在某个区间存在单调区间可转化为不等式有解问题.‎ ‎1．(方向1)(2020·洛阳联考)已知定义域为R的奇函数y＝f(x)的导函数为y＝f′(x)，当x>0时，xf′(x)－f(x)<0，若a＝，b＝，c＝－，则a，b，c的大小关系正确的是(　D　)‎ A．a0时，g′(x)＝<0，∴函数g(x)在(0，＋∞)上单调递减．‎ ‎∵函数f(x)为奇函数，∴函数g(x)是偶函数，∴c＝＝g(－3)＝g(3)，又a＝g(e)，b＝g(ln2)，且3>e>1>ln2>0，∴g(3)0，由f′(x)＝x－<0，得00(或<0)，构造函数F(x)＝f(x)＋g(x)．‎ ‎2．对于不等式f′(x)－g′(x)>0(或<0)，构造函数F(x)＝f(x)－g(x)．‎ 特别地，对于不等式f′(x)>k(或0(或<0)，构造函数F(x)＝f(x)g(x)．‎ ‎4．对于不等式f′(x)g(x)－f(x)g′(x)>0(或<0)，构造函数F(x)＝(g(x)≠0)．‎ ‎5．对于不等式xf′(x)＋f(x)>0(或<0)，构造函数F(x)＝xf(x)．‎ ‎6．对于不等式xf′(x)－f(x)>0(或<0)，构造函数F(x)＝(x≠0)．‎ ‎7．对于不等式f′(x)－f(x)>0(或<0)，构造函数F(x)＝.‎ ‎【典例】　已知定义在R上的可导函数f(x)的导函数为f′(x)，满足f′(x)0.‎ ‎【答案】　B ‎1．已知f(x)的定义域为(0，＋∞)，f′(x)为f(x)的导函数，且满足f(x)<－xf′(x)，则不等式f(x＋1)>(x－1)·f(x2－1)的解集是(　D　)‎ A．(0,1) B．(1，＋∞)‎ C．(1,2) D．(2，＋∞)‎ 解析：因为f(x)＋xf′(x)<0，所以[xf(x)]′<0，故y＝xf(x)在(0，＋∞)上为单调递减函数，由f(x＋1)>(x－1)f(x2－1)，得(x＋1)f(x＋1)>(x＋1)(x－1)·f(x2－1)，即(x＋1)f(x＋1)>(x2－1)f(x2－1)，所以x＋12.‎ ‎2．已知定义域为{x|x≠0}的偶函数f(x)，其导函数为f′(x)，对任意正实数x满足xf′(x)>－‎2f(x)，若g(x)＝x‎2f(x)，则不等式g(x)0时，xf′(x)＋‎2f(x)>0，所以g′(x)>0，所以g(x)在(0，＋∞)上单调递增，又f(x)是偶函数，则g(x)也是偶函数，所以g(x)＝g(|x|)，由g(x)0时，有<0恒成立，则不等式x‎2f(x)>0的解集是(－∞，－2)∪(0,2)．‎ 解析：因为当x>0时，有<0恒成立，即′<0恒成立，所以在(0，＋∞)内单调递减．‎ 因为f(2)＝0，所以在(0,2)内恒有f(x)>0；在(2，＋∞)内恒有f(x)<0.‎ 又因为f(x)是定义在R上的奇函数，所以在(－∞，－2)内恒有f(x)>0；在(－2,0)内恒有f(x)<0.‎ 又不等式x‎2f(x)>0的解集，即不等式f(x)>0的解集．‎ 所以答案为(－∞，－2)∪(0,2)．‎