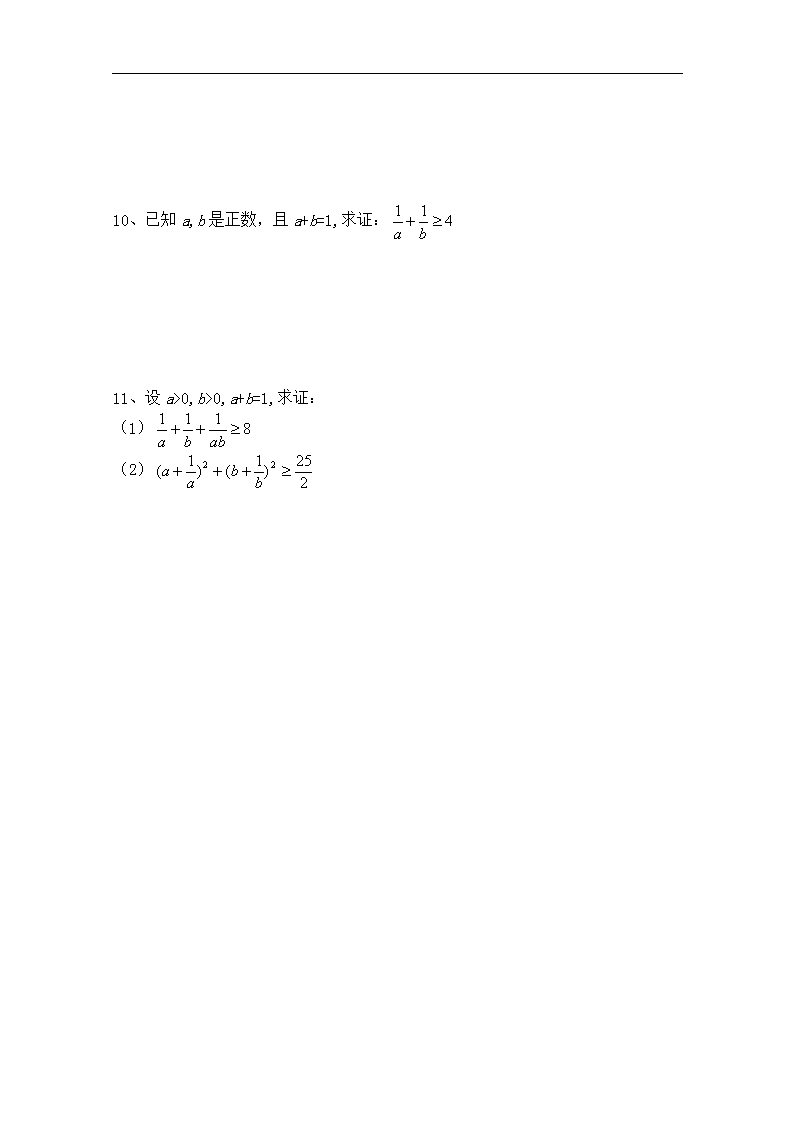- 151.00 KB
- 2021-06-11 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
综合法 同步练习
【选择题】
1、已知函数 ,1
1lg)( x
xxf
若 ,)( baf 则 )( af 等于( )
A、b B、 b C、
b
1 D、
b
1
2、已知函数
12
2)12()(
x
xaxf 是奇函数,那么实数 a 的值等于( )
A、1 B、-1 C、0 D、 1
3、 15cot15tan 等于 ( )
A、2 B、 32 C、4 D、
3
34
4、综合法是( )
A、执果索因的逆推法
B、执因导果的顺推法
C、因果分别互推的两头凑法
D、原命题的证明方法
5、a>0,b>0,则下列不等式中不成立的是( )
A、 221
ab
ba
B、 4)11)((
baba
C、 ba
ab
ba 22
D、 abba
ab
2
【填空题】
6 、 若 00,b>0,且满足 baab 1 ,则 a+b 的最小值为_____________.
8、设 ,12,0,0
2
2 baba 则 21 ba 的最大值为______________.
【解答题】
9、若 ),0,,,(1 bayxbay
b
x
a 且 求证: 2)( bayx
10、已知 a,b 是正数,且 a+b=1,求证: 411
ba
11、设 a>0,b>0,a+b=1,求证:
(1) 8111
abba
(2)
2
25)1()1( 22
bbaa
参考答案
1、B 2、A 3、C 4、B 5、D
6、a+b
7、 222
8、
4
23
9、 ,0,,, bayx 且 1
y
b
x
a 。
2)(2))(( baabbay
xb
x
yabay
b
x
ayxyx
原不等式成立。
(本题还有其他解法)
10、 ,, Rba 且 a+b=1,
2
1,2 ababba
4111
abab
ba
ba
.
(本题还有其他解法)
11、. 证明:(1) 1,0,0 baba
abba 21
2
1 ab , 41
ab
841221)11)((111
abababbabaabba
8111
abba
(2)
22
22 baba
则: 2
22
)2(2
baba
2
222
2
)11(
)2
11
(2)1()1( bbaabbaa
bbaa
2
25
2
)121( 2
ab
2
25)1()1( 22
bbaa .
相关文档
- 数学(文)卷·2019届内蒙古赤峰二中高2021-06-119页
- 2021版高考文科数学(北师大版)一轮复2021-06-1112页
- 20届 湖北省高三(5 月)调研模拟考试 2021-06-114页
- 【数学】2020届一轮复习新课改省份2021-06-117页
- 辽宁省大连海湾高级中学2019-20202021-06-117页
- 山东省青岛市58中2019届高三上学期2021-06-1111页
- 湖北省2020届高三下学期4月月考仿2021-06-1119页
- 浙江省嘉兴一中2019-2020学年高二42021-06-115页
- 2017-2018学年安徽省亳州市高二上2021-06-1111页
- 2013新课标全国卷Ⅱ(理)数学试题2021-06-1110页