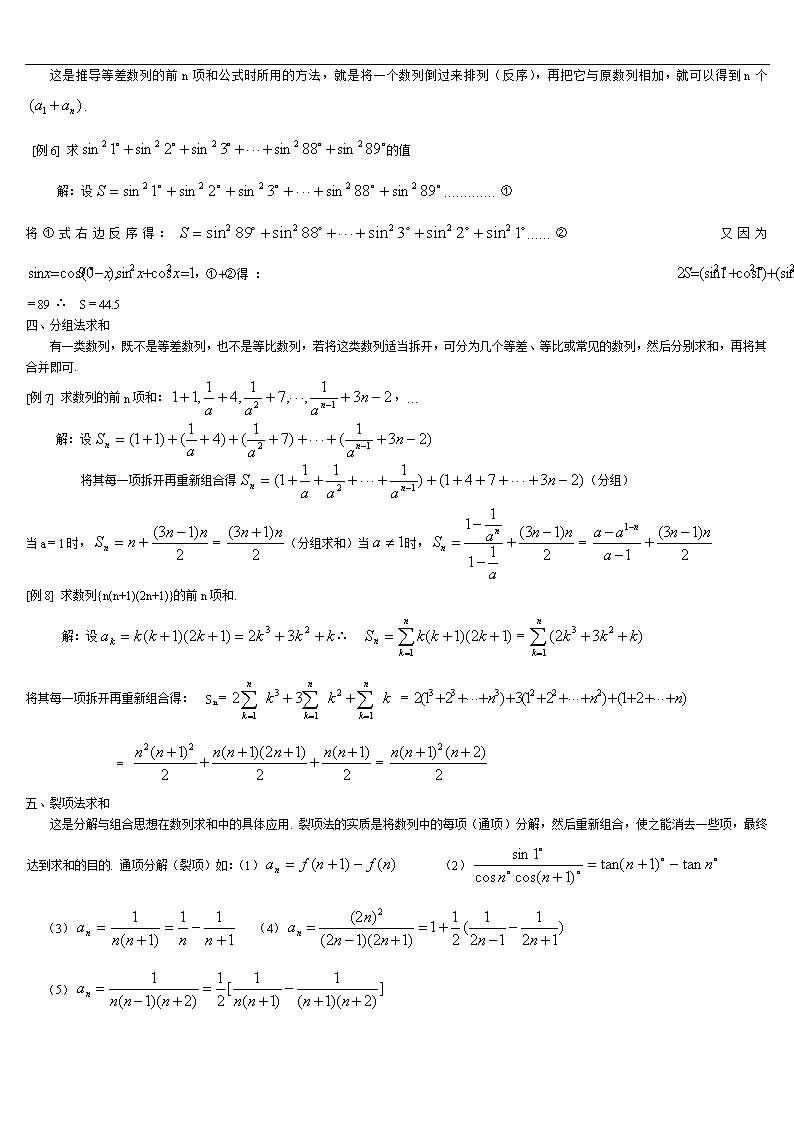高考数学专题复习（精选精讲）练习3-数列求和习题精选精讲 4页

数列求和 一、利用常用求和公式求和 ‎1、等差数列求和公式： 2、等比数列求和公式：‎ ‎ [例1] 已知，求的前n项和.‎ 解：由 由等比数列求和公式得： = ＝＝1－‎ ‎ [例2] 设Sn＝1+2+3+…+n，n∈N*,求的最大值.‎ 解：由等差数列求和公式得 ， ‎ ‎ ∴ ＝＝＝ ∴ 当 ，即n＝8时，‎ 二、错位相减法求和 这种方法是在推导等比数列的前n项和公式时所用的方法，这种方法主要用于求数列{an·　bn}的前n项和，其中{ an }、{ bn }分别是等差数列和等比数列.‎ ‎[例3] 求和：………………………①‎ 解：由题可知，{}的通项是等差数列{2n－1}的通项与等比数列{}的通项之积：设…②（设制错位）‎ ‎①－②得 （错位相减）再利用等比数列的求和公式得：。∴ ‎ ‎[例4] 求数列前n项的和.解：由题可知，{}的通项是等差数列{2n}的通项与等比数列{}的通项之积 设…………………………………①‎ ‎…………② ①－②得 ∴ ‎ 三、倒序相加法求和 这是推导等差数列的前n项和公式时所用的方法，就是将一个数列倒过来排列（反序），再把它与原数列相加，就可以得到n个.‎ ‎ [例6] 求的值 解：设…………. ①‎ 将①式右边反序得：……② 又因为 ，①+②得 ： ＝89 ∴ S＝44.5‎ 四、分组法求和 有一类数列，既不是等差数列，也不是等比数列，若将这类数列适当拆开，可分为几个等差、等比或常见的数列，然后分别求和，再将其合并即可.‎ ‎[例7] 求数列的前n项和：，…‎ 解：设 将其每一项拆开再重新组合得（分组）‎ 当a＝1时，＝（分组求和）当时，＝‎ ‎[例8] 求数列{n(n+1)(2n+1)}的前n项和.‎ 解：设∴ ＝‎ 将其每一项拆开再重新组合得： Sn＝ ＝ ‎ ‎ = ＝‎ 五、裂项法求和 这是分解与组合思想在数列求和中的具体应用. 裂项法的实质是将数列中的每项（通项）分解，然后重新组合，使之能消去一些项，最终达到求和的目的. 通项分解（裂项）如：（1） （2）‎ ‎（3） （4）‎ ‎（5）‎ ‎[例9] 求数列的前n项和.‎ 解：设，则 ‎ ‎＝‎ ‎[例10] 在数列{an}中，，又，求数列{bn}的前n项的和.‎ 解： 　 ∵ ∴ 数列{bn}的前n项和：‎ ‎ ＝ ＝ ‎ ‎ [例11] 求证：‎ 解：设 ‎∵ ＝‎ ‎ ＝＝＝ ∴　原等式成立 例2. 计算： 六、合并法求和 针对一些特殊的数列，将某些项合并在一起就具有某种特殊的性质，因此，在求数列的和时，可将这些项放在一起先求和，然后再求Sn.‎ ‎ [例12] 求cos1°+ cos2°+ cos3°+···+ cos178°+ cos179°的值.‎ 解：设Sn＝ cos1°+ cos2°+ cos3°+···+ cos178°+ cos179°∵ （找特殊性质项）‎ ‎∴Sn＝ （cos1°+ cos179°）+（ cos2°+ cos178°）+ （cos3°+ cos177°）+···+（cos89°+ cos91°）+ cos90°＝ 0 （合并求和）‎ ‎ [例13] 数列{an}：，求S2002.‎ 解：设S2002＝，由可得 ‎……‎ ‎∵ ‎ ‎∴　S2002＝= ‎ ‎=＝＝5‎ ‎[例14] 在各项均为正数的等比数列中，若的值。‎ 解：设 由等比数列的性质 和对数的运算性质 得：‎ ‎ ＝＝＝10‎ 七、利用数列的通项求和 先根据数列的结构及特征进行分析，找出数列的通项及其特征，然后再利用数列的通项揭示的规律来求数列的前n项和，是一个重要的方法.‎ ‎ [例15] 求之和.解：由于 ‎ ‎∴ ＝ ＝＝＝‎ ‎[例16] 已知数列{an}：的值.‎ 解：∵ ＝＝ ＝ ＝‎